| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 21:23 Mar 15 Déc 2009, 21:23 | |
| Oui c'est bon ! Mais là t'a supposer x+y+z#0 Bon tu peux poster ton exo  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 22:04 Mar 15 Déc 2009, 22:04 | |
| -------------------------------------------------------------------------------- bonsoir jé rien supposé ecar si x+y+z=0 donc 0=1... cherchons du hard mnt avec cet exo d'arithmétique!! PROBELme PRoposéTrouver tous les couples (m,n) d"entiers strictement positifs tel que 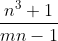 soit entier soit entierEnjoy 
Dernière édition par houssam110 le Mer 16 Déc 2009, 11:31, édité 2 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 22:04 Mar 15 Déc 2009, 22:04 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 22:36 Mar 15 Déc 2009, 22:36 | |
| bonsoir
oui c sa
la fuite ke jé fé dans la démonstration c ke jé fé (z-y)²=16==>z-y=4
et si on discute y-z=4 on aura la 2eme solution !!
faute d'innatention sa sera r&éctifié!
sinn vs voué ke je laisse lexo?!! | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 11:18 Mer 16 Déc 2009, 11:18 | |
| bonjour houssam....
je sais pas ...c'est à Sylphaen de choisir....soit il change son problème puisqu'il est deja posté...soit il accepte ta solution ... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 11:19 Mer 16 Déc 2009, 11:19 | |
| Bon c'est pas grave ^^ On continue avec celui là : Trouver les couples (m,n)...: 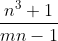 | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 14:59 Mer 16 Déc 2009, 14:59 | |
| solution du problème : prouvons que n et mn-1 sont premiers entre eux: on a m*n-1*(mn-1)=1 donc ∃(x,y)∈Z² tel que xn+y(mn-1)=1 par Bézout on a donc pgcd(n,mn-1)=1 ---------------------------------------------------------------- soit 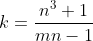 d'autre part on a :n 3(m 3+1)=(m 3n 3-1)+n 3+1 divisons le tout par mn-1 on obtient: }{mn-1}=n^2m^2+nm+1+k) or n et mn-1 sont premiers entre eux alors mn-1 divise m 3+1 alors k est un entier si et seulement si (m 3+1)/(mn-1) l'est..... alors si (n,m) est une solution (m,n) est une solution aussi..... m et n jouent donc un rôle symétrique supposons donc que m≥n... mais : ) alors k=na-1 (avec a £IN) on a m≥n alors : n\leq%201+\frac{1}{n-1}) pour que le dénominateur ne soit pas nul...supposons que n≠1 ------------------------------------------------------------------------ n%3C2) puisque n>1 alors a-1=0<=>a=1 d'où: k=n-1<=>n 3+1=(n-1)(mn-1) d'où : 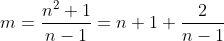 alors n-1 divise 2 d'où n-1=1 ou n-1=2<=>n=2 ou n=3 en remplaçant n par ces deux valeurs dans 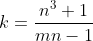 on trouve que n=2--->m=2 ou m=5 et que n=3---->m=5 d'où (n,m)=(2,2);(2,5);(3,5) et comme (m,n) sont aussi solutions : (2,2);(2,5);(3,5);(5,2):(5,3) (1) or on a oublié le cas où n=1  pour n=1 on trouve que m=2 ou m=3 d'où les couples de solutions: (1,2);(2,1);(3,1);(1,3) (2) ------------------------------------------------------------------------- de (1) et (2) on a : S={(1, 2), (1, 3), (2, 1), (2, 2), (2, 5), (3, 1), (3, 5), (5, 2), (5, 3)}sauf erreur.... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 15:31 Mer 16 Déc 2009, 15:31 | |
| salam!! Oui correct Majdouline... A toi ..  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 18:20 Mer 16 Déc 2009, 18:20 | |
| bonsoir à tous  ... problème proposé:soient a,b et c des réels tels que ab,bc et ca sont des nombres rationnels....prouver l'existence des entiers x,y,z qui ne sont pas tous nuls sachant que :ax+by+cz=0have fun  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 19:24 Mer 16 Déc 2009, 19:24 | |
| Bonsoir!!
On a pa bien compris ton Probléme Majdouline
si on prend a,b,c des entiers
on aura ab;bc;ac des entier ==> des nombres rationnels!
on va jamé trouvé un x,y,z dans ce cas tel que ax+by+cz=0 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 19:34 Mer 16 Déc 2009, 19:34 | |
| a,b,c c'est de réels pas des entiers ; donc ab , bc , ac sont pas forcément des rationnels , mais dans l'exo ils le sont ... Le truc c'est de prouver que quelque soit a,b,c des réels tel que ab , bc , ac sont rationnel alors il éxiste des nombres x,y,z tel que : ax + by + cz = 0 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 19:35 Mer 16 Déc 2009, 19:35 | |
| SAlut ! a,b,c entiers ==> a;b;c des réles  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 21:17 Mer 16 Déc 2009, 21:17 | |
| - houssam110 a écrit:
- Bonsoir!!
On a pa bien compris ton Probléme Majdouline
si on prend a,b,c des entiers
on aura ab;bc;ac des entier ==> des nombres rationnels!
on va jamé trouvé un x,y,z dans ce cas tel que ax+by+cz=0 si a,b et c sont des entiers on peut trouver x y et z il suffit de prendre x=b+c y=-a et z=-a mais les gars...si je continue à expliquer je vais répondre au problème  P.S. je crois que la solution est bcp plus simple que vous imaginez!!!! | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 22:16 Mer 16 Déc 2009, 22:16 | |
| si on prends a,b,c des reel strict positives donc ax+by+cz#0 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 16 Déc 2009, 22:33 Mer 16 Déc 2009, 22:33 | |
| bonsoir !
Solution (sauf erreur)
soit (u,v,r,t,n,m¨) £ Z^6 et a;b;c #0
tel que
ab =u/v et ac=r/t et bc=n/m
bc/ac =nt/mr=b/a
bc/ab=nv/mu=c/a
donc on doit montrer lexistence de x;y;z tels que
ax+by+cz=0
<==> x+by/a +cz/a =0
<==> x+nty/mr +nvz/mu=0
<==> xmru+ntyu+nvzr=0
on peut prendre le cas de z=0 et x=nt et y=-mr
==>conclusion
si a ou b ou c=0
par symetrie soit a =0
donc on a comme solution
x=1 ;y=0;z=0
... | |
|
  | |
smash
Maître

 Nombre de messages : 129 Nombre de messages : 129
Age : 31
Localisation : In Your Heart
Date d'inscription : 09/05/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 07:39 Jeu 17 Déc 2009, 07:39 | |
| - majdouline a écrit:
- houssam110 a écrit:
- Bonsoir!!
On a pa bien compris ton Probléme Majdouline
si on prend a,b,c des entiers
on aura ab;bc;ac des entier ==> des nombres rationnels!
on va jamé trouvé un x,y,z dans ce cas tel que ax+by+cz=0 si a,b et c sont des entiers
on peut trouver x y et z
il suffit de prendre x=b+c y=-a et z=-a
mais les gars...si je continue à expliquer je vais répondre au problème 
P.S. je crois que la solution est bcp plus simple que vous imaginez!!!! Pourriez vous prouver que : b+c # 0 ou -a # 0 afin de respecter la consigne? | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 09:44 Jeu 17 Déc 2009, 09:44 | |
| Bonjour psuike je seré occupé cette journée jvé poster un exo (si ma solution été fausse vs refuser léxo sélllé correct vs laccpeté) PROBLEMe PRoposéRésoudre dasn IR 4x²-40[x]+51=0 PS [] ==> partie entire  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 12:23 Jeu 17 Déc 2009, 12:23 | |
| - marouan777 a écrit:
- si on prends a,b,c des reel strict positives donc ax+by+cz#0
marouan stp on parle pas de a b et c ..on parle de x y et z.... | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 12:35 Jeu 17 Déc 2009, 12:35 | |
| - smash a écrit:
Pourriez vous prouver que : b+c # 0 ou -a # 0 afin de respecter la consigne? lol ...élimine donc ce cas on fait la négation supposons que b+c=0 et a=0... tu trouveras xb-yc=0 il suufit donc de prendre x=c et y=b une fois ce cas est éliminé on suppose que b+c # 0 ou -a # 0 et on continue..... | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 12:41 Jeu 17 Déc 2009, 12:41 | |
| salam.... la solution de houssam est correcte...cherchez sonc la solution de son exo  !!!!!c'est un problème assez simple  !!! | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 16:43 Jeu 17 Déc 2009, 16:43 | |
|
Dernière édition par reda-t le Jeu 17 Déc 2009, 17:23, édité 2 fois (Raison : connerie) | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 16:49 Jeu 17 Déc 2009, 16:49 | |
| Bonjour
solution fausse!..
contre exemple k=3 ==> x=V69/2
donc 4.69/4-40[V69/2]+51=0 ?? | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 17:32 Jeu 17 Déc 2009, 17:32 | |
| salam.... un problème assez simple est encore sans solution  ....je poste donc ma solution solution du problème:première remarque [x] ne pet pas être négatif sinon 4x²-40[x]+51 est tjs strictement positif.....[x]>0<=>x£IR+ [x]+1>x≥[x]<=>4[x]²-32[x]+55>4x²-40[x]+51≥4[x]²-40[x]+51 <=>4[x]²-32[x]+51>0 et 4[x]²-40[x]+51≤0 pour :4[x]²-32[x]+55>0 delta=12² les deux racines sont [x]=11/2 ou [x]=5/2 puisque 4[x]²-32[x]+55>0 alors [x]∈]-00,2.5[∪]11/2,+00[ or [x]£IN alors [x]∈ [0,2]∪[6,+00[ (1)---------------------------------------------------------- pour 4[x]²-40[x]+51≤0 delta=28² les deux racines sont [x]=17/2 ou [x]=3/2 puisque 4[x]²-40[x]+51≤0 alors [x]∈[3/2,17/2] or [x]£IN alors [x]∈[2,8] (2)------------------------------------------------------------- de (1) et (2) on a :[x]∈[6,8]∪{2} d'où [x]=2 ou [x]=6 ou [x]=7 ou [x]=8 pour [x]=2 et en revenant à l'équation:4x²-40[x]+51=0 on trouve que x=V29/2----------------------------------------------------------------------- pour [x]=6 et en revenant à l'équation:4x²-40[x]+51=0 on trouve que x=3V21/2------------------------------------------------------------- pour[x]=7 et en revenant à l'équation:4x²-40[x]+51=0 on trouve que : x=V229/2------------------------------------------------------------- pour [x]=8 et en revenant à l'équation:4x²-40[x]+51=0 on trouve que x=V269/2-------------------------------------------------------------------- d'où S={V29/2,3V21/2,V229/2,V269/2}sauf erreur.....
Dernière édition par majdouline le Jeu 17 Déc 2009, 17:45, édité 2 fois | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 17:38 Jeu 17 Déc 2009, 17:38 | |
| Salut Majdouline!!
IL te manque une solution ... | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 17:46 Jeu 17 Déc 2009, 17:46 | |
| voilà houssam...une petite erreur de calcul...mais c'est rectifié maintenant  .... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
