| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 19:59 Lun 14 Déc 2009, 19:59 | |
| correct houssam  ...à toi de poster un exo!!!! | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 20:02 Lun 14 Déc 2009, 20:02 | |
| MErci Majoudline c un joli exercice il ma pris du temps ^^ bon PROBLEM proposé a,b,c>0 Montrer Algébriquement et sans théorémes cela 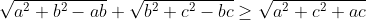 | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 20:12 Lun 14 Déc 2009, 20:12 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 20:15 Lun 14 Déc 2009, 20:15 | |
| oué merci pour le lien PErelman dabord (ke jé déja vu ^^) cela est un jeu et jé donné une conditon pour résoudre cet exo (sans théoremes et algébriquement!!)  merci pour l'intervention !! | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 20:23 Lun 14 Déc 2009, 20:23 | |
| Re dsl j'ai oublier le ² , j'ai trouvé une autre pour montrer que f(0)=0 mais ta solution Houssam est suffisante ^^ | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 20:46 Lun 14 Déc 2009, 20:46 | |
| Solution :
on a l'inégalité équivalente à :
V(a²+b²-ab) + 2V(b²+c²-bc) >= V(a²+c²+ac) + V(b²+c²-bc)
(a²+b²-ab)+4(b²+c²-bc)+4V(a²+b²-ab)(b²+c²-bc) >= a²+c²+ac+b²+c²-bc+2V(a²+c²+ac)(b²+c²-bc)
il est tres facile de montrer que :
a²+c²+ac+b²+c²-bc >= 2V(a²+c²+ac)(b²+c²-bc)
et que : 4V(a²+b²-ab)(b²+c²-bc) >= b²+ ab+bc+ac
donc il suffit de prouver que :
3b² >= a²+ac+ab
sans nuire la généralité du probleme on suppose que b >= a et b>= c
donc b²>= a² , b²>= ac , b²>= ab
en sommant on trouve le résultat désiré | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 21:10 Lun 14 Déc 2009, 21:10 | |
| je crois samix que t’as pas le droit de supposer que b=max{a,b,c}…
en effet…si on le fait ça devient trivial :
-a>-b<=>-ab>-b² <=>a²+b²-ab>a²<=>V(a²+b²-ab)>a
-c>-b<=>-cb>-b²<=>b²+c²-cb>c²<=>V(b²+c²-bc)>c
En sommant on trouve que
V(a²+b²-ab) + V(b²+c²-bc) >=a+c>V(a²+c²+ac)
P.S. la non permission de cette considération vient du fait que les variables ne jouent ni un rôle symétrique ni cyclique..... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 21:14 Lun 14 Déc 2009, 21:14 | |
| - samix a écrit:
- Solution :
on a l'inégalité équivalente à :
V(a²+b²-ab) + 2V(b²+c²-bc) >= V(a²+c²+ac) + V(b²+c²-bc)
(a²+b²-ab)+4(b²+c²-bc)+4V(a²+b²-ab)(b²+c²-bc) >= a²+c²+ac+b²+c²-bc+2V(a²+c²+ac)(b²+c²-bc)
il est tres facile de montrer que :
a²+c²+ac+b²+c²-bc >= 2V(a²+c²+ac)(b²+c²-bc)
et que : 4V(a²+b²-ab)(b²+c²-bc) >= b²+ ab+bc+ac
donc il suffit de prouver que :
3b² >= a²+ac+ab
sans nuire la généralité du probleme on suppose que b >= a et b>= c
donc b²>= a² , b²>= ac , b²>= ab
en sommant on trouve le résultat désiré bonsoir !! jé po compris ckyé en rouge en cki concerne ta considération je vois ke c po valable un simple controexemple peu te la démontrer b=1 a=2 c=1 | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 21:31 Lun 14 Déc 2009, 21:31 | |
| houssam...je crois que ce qui est en rouge est vraiment facile à prouver:
4(a²+b²-ab)>=(a+b)² (vaut mieux de ne pas expliquer des choses triviales)
4(b²+c²-bc)>=(b+c)²(aussi sans explication)
en mutlipliant les deux inégalités on trouve que :
16(a²+b²-ab)(b²+c²-bc)>=(a+b)²(b+c)²
<=>4V(a²+b²-ab)(b²+c²-bc) >=(a+b)(b+c)=b²+ab+bc+ca
la seule erreur commise par samix est l considération b=max{a,b,c}.... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 21:36 Lun 14 Déc 2009, 21:36 | |
| Oui je vois!!
cété le juguement de 1ere vue !!
MErci qd meme !! | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 22:28 Lun 14 Déc 2009, 22:28 | |
| on devlevant on trouve ala fin 3(ab-bc-ac)² | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 22:32 Lun 14 Déc 2009, 22:32 | |
| nn je crois qu'à la fin on trouve (ab+bc-ca)²>=0 | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 22:36 Lun 14 Déc 2009, 22:36 | |
| solution du problème proposé:
on fait le carré...l'inégalité équivaut à:
2V[(b²+c²-bc)(a²+b²-ab)]>=ab+bc+ca-2b²
encore le carré:
4(b²+c²-bc)(a²+b²-ab)>=(ab+bc+ca-2b²)²
<=>3a²b²+3b²c²+3a²c²+6ab²c>=6a²bc+6abc² (juste le développement+calculs)
<=>a²b²+b²c²+a²c²+2ab²c>=2a²bc+2abc²
<=>(ab+bc-ac)²>=0
ce qui est tjs vrai.....
sauf erreur.... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 14 Déc 2009, 22:58 Lun 14 Déc 2009, 22:58 | |
| Oui correct ...  (c chaud les calculs ^^) poste ton exo..  | |
|
  | |
Emerson
Maître

 Nombre de messages : 106 Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 00:14 Mar 15 Déc 2009, 00:14 | |
| vasy postez le suivant... | |
|
  | |
stranger
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 13/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 12:18 Mar 15 Déc 2009, 12:18 | |
| on peut mq: 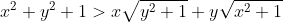 avec am.gm | |
|
  | |
stranger
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 13/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 12:28 Mar 15 Déc 2009, 12:28 | |
| ya qq pour mq 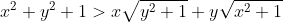 avec AM.GM,? | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 12:41 Mar 15 Déc 2009, 12:41 | |
| 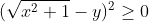 D'où : 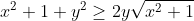 en sommant on trouve le résultat voulu. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 12:51 Mar 15 Déc 2009, 12:51 | |
| problème proposé:
trouver tous les couples (m,n) d'entiers naturels qui satisfont l'équation:
(m+n)4=m²n²+m²+n²+6mn
P.S.dsl de proposer un problème si facile....car j'ai pas un grand choix d'exos.... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 13:53 Mar 15 Déc 2009, 13:53 | |
| (m+n)4=m4+n4+6m²n²+4mn(m²+n²)
Si : m>1 et n>1 alors :
(m+n)4>m²+n²+6mn+m²n²
Psk : Si n>1 donc n4>n² et 6m²n²>6mn et
4mn(m²+n²)>m²+n²
Si : m<=1 où n<=1
Cas 1 :
m=1
L'équation devient :
n4+6n²+4n(n+1)+1=n²+6n+n²+1
n4+4n²+4n(n²+1)=6n
D'où : n=0
Car 4n(n²+1)>=4n.2n=8n²>=8n>=6n
Si m=0
L'équation devient :
n4=n²
n²(n²-1)=0
n²=1 ou n²=0
n=1 ou n=0
Alors :
S={(0.0)(0.1)(1.0)} | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 14:21 Mar 15 Déc 2009, 14:21 | |
| salut!!
on a (m+n)^4=m^4+n^4+6m²n²+4mn(m²+n²)
si m>=1 et n>=1
donc
m^4>=m² et n^4>=n²
et 4mn(m²+n²)>8mn (car m²+n²>2)
et 6m²n²>m²n²
donc m^4+n^4+4mn(m²+n²)+6m²n²>n²+m²+8mn+m²n²>n²+m²+6mn+m²n²
cky² absurde
donc n=0 ou m=0
si n=0
alors m^4=m²==> m=0 ou m=1
si m=0==> n^4=n²==>n=0ou n=1
S={(0.0);(1.0);(0.1)} | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 18:37 Mar 15 Déc 2009, 18:37 | |
| bonsoir  ... dsl pour le retard de la confirmation....je viens juste de lire vos solutions.... les deux sont correctes...mais Sylphaen etait le plus rapide...allez Sylphaen poste nous un exo  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 18:53 Mar 15 Déc 2009, 18:53 | |
| oué c sa poste ns un exo sylphaen !! PS: tu dois réviser ton début !!  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 20:14 Mar 15 Déc 2009, 20:14 | |
| Trouvez tous les réels x,y,z tels que :
x²-yz=4
y²-zx=3
z²-xy=5
| |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Déc 2009, 21:15 Mar 15 Déc 2009, 21:15 | |
| Salut c assez facile ...
Solution (sauf erreur!!
on a x²-y²-yz+zx=1
==> (x-y)(x+y+z)=1
et d'une autre part on a :
z²-x²-xy+yz=1
==>(z-x)(x+y+z)=1
donc z-x=x-y ==> (z+y)/2 =x
et aussi de meme on trouve
(z-y)(x+y+z)=2 (3)
apres on remplace dans le systeme et c facile !!
on aura
x²-yz=4==> (z+y)²/4 -yz=4 ==> z²+y²/4 -yz/2=4
==> z²+y²=16+2yz
==> z-y=4 ou z-y=-4
en remplaçant dans (3) ==> x+y+z=1/2 ==> 3(y+z)/2=1/2
==> y+z=1/3
donc 2z=4+1/3 ==> z=13/6
donc z-y=4 ==> y=-11/6
x=(y+z)/2 ==> x=1/6
et on fait de meme pour
y-z=4 on trouve les solutions siuvantes ;x=-1/6 y=11/6 ;z=-13/6
donc S={(1/6.-11/6.13/6);(-1/6.11/6.-13/6)}
Dernière édition par houssam110 le Mar 15 Déc 2009, 22:23, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
