Olympiodiose

Euh quelqu'un peut me dire c'est quoi la faute dans ma 2éme réponse ?

moi aussi je vois pas la faute dans ma réponse c'est trop simple :

on a : (x3+y3)(y3+z3)(z3+x3)= (x+y)3(y+z)3(z+x)3=(xyz)3

si x=y=z=0 c'est juste

donc si x différent de 0 ou y différent de 0 ou z différent de 0 c'est faut

la premiére c'est P la deuxiéme c'est 7P

on en conclu que xyz= 0

Mais elle est correcte pour :

x=-y=1 z=0

x=-y=2 z=0
...
Donc pas forcément x=y=z=0

Ok mais c'est pas ce qui est demandé enfin de compte on a prouvé que xyz = 0 XD

Oui , mais bon tu étudie seulement le cas x=y=z=0

bonsoir...
vous voulez donc que je vous indique vos fautes.....bien sur

Sylphaen a écrit:

Bon si on part du 1er résultat on aura :

(x+y)²(y+z)²(x+z)²=(x²-xy+y²)(x²-xz+z²)(y²-yz+z²)

(x+y)² >= 4xy
Donc :

(x+y)²(y+z)²(x+z)² >= 4^(3) (xyz)^(2)

car (x+y)²(y+z)²(x+z)² >= 0


Alors on aura :

(x²-xy+y²)(x²-xz+z²)(y²-yz+z²) >= 64(xyz)^(2)
et : (x²-xy+y²)(x²-xz+z²)(y²-yz+z²) >=0
Supposons que : x#-y et x#-z et y#-z

Alors on aura :





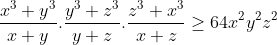
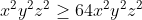
(xyz)²=0

Et on supposant le contraire on aura : x=-y ou x=-z ou y=-z

alors (x+y)(x+z)(y+z)=0=xyz

On espérons de ne pas faire une autre faute :p

tu as ecris :
(x+y)²>=4xy
(y+z)²>=4yz
(x+z)²>=4xz
on multipliant les 3 inégalités on obtient: (x+y)²(y+z)²(x+z)² >= 4^(3) (xyz)^(2)
mais t'as oublié si l'un des RHS est négatif ...ainsi l'inégalité sera bouleversée
----------------------------------------------------------------------

marouane777 a écrit:

( x²+y²-xy)(y²+z²-yz)(x²+z²-xz)>= (xyz)².

c'est pas tjs vrai et si par exemple:xy=<0..ainsi l'inégalité ne sera plus vraie ...
à darkpseudo....
vraiment ta logique est exceptionnellement fausse...
tu mélange un peu....entre le ou et le et
par exemple pour résoudre:x²=1 pour x=1 1=1
supposons que x différent de 1....c'est faux car P est vraie...
mais nn ce raisonnement est strictement faux.....car x peut être égal à -1!!!!!!!!!!!!!!!!!!!!!!!
ici on parle des valeurs de xyz...on parle de ou est nn pas et
xyz=0 c'est vrai mais pourquoi pas ajouter xyz=0 ou xyz=r et ça restera vrai !!!!
esperons que vous m'avez compris tous!!!!
amicalement!!!!!!!!!!!!!!!!!!!!!!!!!!
P.S.cherchez encore la bonne solution...enfin la bonne méthode (car c'est vrai xyz=0)

deleted

BSr !!
sauf erreur car ya bcp de calculs !!
soit x et y et z des nombre tels que x tokhalif -z
et y tokhalif -z
et x tokhalif -y
(dsl si jé copié ton début marouane!!)
(x3+y3)(y3+z3)(z3+x3)=xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz).
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=0 ==> xyz=0
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)#0
on a (x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)² (1)
posons x+y=a et y+z=b et x+z=c
(1)<==> (a²-3xy)(b²-3yz)( c²-3xz)=x²y²z²
<==>
a²b²c²-3a²b²xz-3a²yzc²+9a²yzx²-3c²b²xy+9b²xyz²+9c²xy²z-27x²y²z²=x²y²z²

<==> -3a²b²xz-3a²yzc²+9a²yzx²-3c²b²xy+9b²xyz²+9c²xy²z-27x²y²z²=0 (1)
et on a ab=xyz/c et ac=xyz/b et bc=xyz/a
donc (1)
<==> xyz(-x²yz²/c²-y²z²x/b²+3a²z-x²y²z/a²+3b²z+3c²y-9xyz)=0
==> xyz=0 ou (-x²yz²/c²-y²z²x/b²+3a²z-x²y²z/a²+3b²z+3c²y-9xyz)=0
pour la 2eme c facile!!
ala fin xyz=0
on revient a ckon a dit au début
si x=-y ou x=-z ou y=-z
alors xyz=0 car x+y=0!!
par exemple !!

houssam110 a écrit:

BSr !!
sauf erreur car ya bcp de calculs !!
soit x et y et z des nombre tels que x tokhalif -z
et y tokhalif -z
et x tokhalif -y
(dsl si jé copié ton début marouane!!)
(x3+y3)(y3+z3)(z3+x3)=xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz).
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=0 ==> xyz=0
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)#0
on a (x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)² (1)
posons x+y=a et y+z=b et x+z=c
(1)<==> (a²+3xy)(b²+3yz)( c²+3xz)=x²y²z²
<==> a²b²c²+3a²b²xz+3a²c²yz+9a²z²xy+3c²b²xy+9b²z²xy+9c²y²xz+27x²y²z²=x²y²z²
<==> a²b²xz+a²c²yz+3a²z²xy+c²b²xy+3b²z²xy+3c²y²xz+9x²y²z²=0 (a²b²c²=x²z²y²)
et on a ab=xyz/c et ac=xyz/b et bc=xyz/a
donc (1)
<==> xyz(x²yz²/c²+y²z²x/b² +3a²z+x²y²z/a² +3b²z+3c²y+9x²y²z²)=0
==> xyz=0 ou x²z²y/c² +y²z²x /b² +3a²z+x²y²z/a² +3b²z+3c²y+9x²y²z²=0
==> xyz=0 ou xyz(xz/c² +yz/b² +xy/a²+9xyz)+3a²z+3b²z+3c²y=0
pour la 2eme il suffit de taw7id lma9amate !!
ala fin xyz=0
on revient a ckon a dit au début
si x=-y ou x=-z ou y=-z
alors xyz=0 car x+y=0!!

je crois qu'aux places des + il te faut des -

jé corrigé jespere ke jme suis po trompé ya bcp de calculs !!

houssam110 a écrit:

BSr !!
sauf erreur car ya bcp de calculs !!
soit x et y et z des nombre tels que x tokhalif -z
et y tokhalif -z
et x tokhalif -y
(dsl si jé copié ton début marouane!!)
(x3+y3)(y3+z3)(z3+x3)=xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz).
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=0 ==> xyz=0
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)#0
on a (x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)² (1)
posons x+y=a et y+z=b et x+z=c
(1)<==> (a²-3xy)(b²-3yz)( c²-3xz)=x²y²z²
<==>
a²b²c²-3a²b²xz-3a²yzc²+9a²yzx²-3c²b²xy+9b²xyz²+9c²xy²z-27x²y²z²=x²y²z²

<==> -3a²b²xz-3a²yzc²+9a²yzx²-3c²b²xy+9b²xyz²+9c²xy²z-27x²y²z²=0 (1)
et on a ab=xyz/c et ac=xyz/b et bc=xyz/a
donc (1)
<==> xyz(-x²yz²/c²-y²z²x/b²+3a²z-x²y²z/a²+3b²z+3c²y-9xyz)=0
==> xyz=0 ou (-x²yz²/c²-y²z²x/b²+3a²z-x²y²z/a²+3b²z+3c²y-9xyz)=0
pour la 2eme c facile!!
ala fin xyz=0
on revient a ckon a dit au début
si x=-y ou x=-z ou y=-z
alors xyz=0 car x+y=0!!
par exemple !!

démontre que la deuxième est facile donc !!!!

je crois qu'il est temps de poster une solution...
solution du problème:
supposons que xyz≠0 (<=>x,y,z≠0)
depuis les deux égalités on a :
(x²-xy+y²)(y²-yz+z²)(x²-xz+z²)=x²y²z²
ce qui équivaut à :

implique: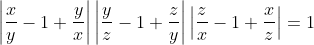

il est facile de démontrer que :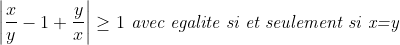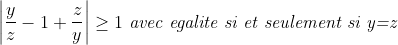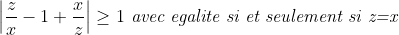



supposons donc x≠y≠z on trouvera que les trois précédentes inégalités sont strictement supérieurs à 1 ...ce qui implique que :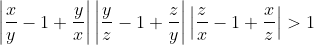

ce qui est absurde alors au moins deux nombres sont égaux....par symétrie de rôles supposons que ces deux nombres sont x et y...x=y
alors (x+y)(y+z)(z+x)=xyz devient: 2x(x+z)²=x²z<=>2(x+z)²=xz
première remarque xz>0 or on a 2(x+z)²≥8xz>xz
ce qui est absurde
notre supposition est donc fausse d'où xyz=0
sauf erreur....

Bonjour !!
désolé si jé po répondu a ton message car jété tres occupé ainsi que je me suis trompé de signe ckya tout changé !!
^pour ta solution je pense qu'il faut po dir k'au moins 2 nombres sont egaux mais plutot tout les nombre sont egaux cky donne 8x^3=x^3==> x =0 ==> contradition
car si x=y et z≠x et y≠z on aura
|x/z -1 +z/x| >1 (car on a pa le cas dégalité!!)
et |y/z -1+z/y|>1 (car on a po le cas dégalité
donc |x/z -1 +z/x||y/z -1 +z/y|>1
et on a |x/y -1 +y/x|=1 donc |x/z -1 +z/x||y/z -1 +z/y|=1 ...

houssam110 a écrit:

pour ta solution je pense qu'il faut po dir k'au moins 2 nombres sont egaux mais plutot tout les nombre sont egaux

siii... on peut le dire...en effet:
j'ai supposé que x≠y≠z j'ai trouvé une contradiction..ce qui donne x=y ou y=z ou z=x(et nn pas x=y et x=z et y=z).....ce qui équivaut à au moins deux nombres sont égaux ...et encore une contradiction...ce qui veut dire que la proposition xyz≠0 est fausse....CQFD....ma solution reste donc tjs correcte!!!!!
sauf erreur......

SAlut !!
dapres cke je pesne :
pour avoir |x/y -1+y/x||x/z -1 +z/x||y/z -1 +z/y|=1
ifo ke x=y et y=z et z=x (prendre le cas dégalité de chake inégalité)!!
et si on fé cke tu dis x=y ou y=z ou z=x
on peut avoir x=y et y≠z et z≠x
comme sa on aura jamé |x/y -1+y/x||x/z -1 +z/x||y/z -1 +z/y|=1
car on aura |x/z -1 +z/x||y/z -1 +z/y|>1

...

Bonsoir!
mais sa reste correct vu que x=z ou z=x ou y=z contient x=y et y tokhalif z et z tokhalif x
mais ta choisi un chemin long !!

Salùt !

Solution du Probléme de Majdouline :

si x,y et z positifs alors x=y=z=0( il suffit de de developper le membre gauche )
on peut supposer que x et y positifs . et z négatif.
si xyz#0 alors on peut diviser les deux egalites membre à membre et on trouve :
(x²-xy+y²)(y²-yz+z²)(x²-xz+z²)=x²y²z²
xy.3|xz|.3|zy |<= (xyz)² ie 9(xyz)²<=(xyz)²
ce qui est Absurde donc xyz=0 .

A+!

ok ...je vais poster un nouveau problème:
trouver toutes les fonctions de IR---->IR sachant que :
f(x.f(x)+f(y))=(f(x))²+y
P.S.ta solution ayoub est correcte ...mais t'as du la poster avant que je poste la mienne.....

Supposons que f(x)#0
Donc :
f(x.f(x)+f(y))#0
f(x)²+y#0
Ce qui est faux en prenons y=-f(x)²
Donc il est existe un x£[R tels que f(x)=0

On met :
x=y=0 alors
f(f(0))=f(0)² (*)
On met :
f(x)=0
alors :
f(f(y))=y (**)

f(f(x.f(x)+f(y)))=x.f(x)+f(y)

f(f(x)²+y)=x.f(x)+f(y)
et on a :
f(x.f(x)+f(y))=f(x)²+y

En additionnons :
f(f(x)²+y)+f(x.f(x)+f(y))=(f(x)²+y)+(x.f(x)+f(y))

Donc :
On peut remarquer qu'on a f(x)=x
Puis reste à trouver d'autres

SAlut !!
voici cke jé trouvé (Sauf erreur ...)
1) (montrer que f est injective!
pour x=0 et f(0)=a
on a f(f(y))=a²+y
soi c et de de IR
donc f(c)=f(d)==> f(f(c))=f(f(d))==> a²+c=a²+d==> c=d
donc f est injective
-----------------------------------------
2) chercher f(0)
on a f(x)=-f(-x) (1)
<==> xf(x)=-x.f(-x)
<==> x.f(x)+f(y)=-xf(-x)+f(y) (2)
<==> f(xf(x)+f(y))=f(-x.f(-x)+f(y)) (3)
<==> f(x)²+y=f(-x)²+y
<==> f(x)²=f(-x)²
ceci est correct pour x=0
donc f(0)=-f(0)==> f(0)=0
PS: ya une ékivalence de (3)--> (2) car f est injective!!
-----------------------------------------
3) trouver les solutions!
on a f(0)=0 donc f(f(y))=y (en remplaçant x par 0)
et on a f(xf(x))=f(x)² (en remplaçant y par 0)
donc f(f(x).f(f(x)))=f(f(x))²
==>f(xf(x))=x²
donc f(x)²=x²
==> f(x)= x ou f(x)=-x
en vérifiant on trouve ke c correct
...
PS: f(x)²=(f(x))²

Sylphaen a écrit:

Supposons que f(x)#0
Donc :
f(x.f(x)+f(y))#0
f(x)²+y#0
Ce qui est faux en prenons y=-f(x)²
Donc il est existe un x£[R tels que f(x)=0

On met :
x=y=0 alors
f(f(0))=f(0)² (*)
On met :
f(x)=0
alors :
f(f(y))=y (**)

f(f(x.f(x)+f(y)))=x.f(x)+f(y)

f(f(x)²+y)=x.f(x)+f(y)
et on a :
f(x.f(x)+f(y))=f(x)²+y

En additionnons :
f(f(x)²+y)+f(x.f(x)+f(y))=(f(x)²+y)+(x.f(x)+f(y))

Donc :
On peut remarquer qu'on a f(x)=x
Puis reste à trouver d'autres

Oui je comprend il rest de trouver d'autre !!
sinn sa se voit car ton message est édité

f(f(x).f(f(x)))=f(f(x))²==>f(xf(x))=x²
J'ai pas compris le passage tu peux expliquer stp ^^

car f(f(x))=x !!

..dsl..

C faux Juste ABdess!!
car f(a)=a²