| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 | |
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 09 Déc 2009, 12:12 Mer 09 Déc 2009, 12:12 | |
| solution du problème(sauf erreur):^{2}(xy-1)^{2}+\sqrt{y^{2}-x^{2}}=0) <=> ^{2}(xy-1)^{2}=0) %20\textit{%20et%20}%20(x^{2}+y^{2}-4)^{2}(xy-1)^{2}=0\Leftrightarrow%20(x=y\textit{%20et%20}x^{2}+y^{2}-4)^{2}(xy-1)^{2}=0)\textit{%20ou%20}(x=-y%20\textit{%20et%20}(x^{2}+y^{2}-4)^{2}(xy-1)^{2}=0)) si x=y et (x²+y²-4)²(xy-1)²=0 =>(2x²-4)²(x²-1)²=0 <=>2x²-4=0 ou x²=1<=>x=y=V2 ou x=y=-V2ou x=y=1 ou x=y=-1 d'où les couples suivants de solutions: (V2,V2);(-V2,-V2);(1,1);(-1,-1) (1) ------------------------------------------------------------------------------------ si x=-y et (x²+y²-4)²(xy-1)²=0=>(2x²-4)²(-x²-1)²=0 <=>2x²-4=0 ou x²+1=0(impossible) alors 2x²-4=0 d'où x=V2et y=-V2 ou x=-V2 et y=V2 d'où les deux couples des solutions: (V2,-V2);(-V2,V2) (2) -------------------------------------------------------------------- de (1) et (2) on a : S={(V2,V2);(-V2,-V2);(1,1);(-1,-1);(V2,-V2);(-V2,V2)} | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 09 Déc 2009, 12:58 Mer 09 Déc 2009, 12:58 | |
| | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 09 Déc 2009, 13:01 Mer 09 Déc 2009, 13:01 | |
| oui majdouline poste ton exo | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 11:19 Jeu 10 Déc 2009, 11:19 | |
| On : 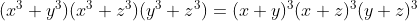 Et on sait que : 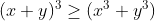 Si x,y ne sont pas tous les deux négative et |x|>=|y| Et le contraire si l'un d'eux est négative . De même pour le reste .. Alors on aura : 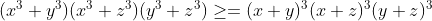 ou 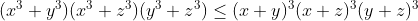 Cas d'égalité seulement si : xy(x+y) =xz(x+z)=yz(y+z)=0 [ x=0 ou y=0 ou y=-x ] Et [ x=0 ou z=0 ou z=-x ] Et [ y=0 ou z=0 ou z=-y ] Alors au moins l'un d'eux est égal à 0 . Donc : xyz = 0 .
Voilà, Puisque je suis une machine à erreur ^^ j'attends une confirmation 
Dernière édition par Sylphaen le Jeu 10 Déc 2009, 11:34, édité 2 fois | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 11:30 Jeu 10 Déc 2009, 11:30 | |
| Re
je pense que ta solution n'est pas correcte car x ,y, z des réés
prend x = -1 et y =-1
-8 superieur à -2 ce qui est faux
donc on peux pas dire que (x+y)^3 sup ou égal à x^3+y^3 | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 11:32 Jeu 10 Déc 2009, 11:32 | |
| Oué je l'avais édité ..
Ca si x,y ne sont pas les 2 négative . ou bien c'est |x|>=|y| et x>0>y
Je sais c'est faux lol ^^
J'refais >.<
Puis reste étudié le cas ou les deux sont négative ..
Je fais ce cas ^^
Dernière édition par Sylphaen le Jeu 10 Déc 2009, 11:37, édité 1 fois | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 11:36 Jeu 10 Déc 2009, 11:36 | |
| Re
et si x est negative et y est positive ..
et tu ne peux pas etudier seulement le cas de x et y , tu a oublié le z.. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 11:38 Jeu 10 Déc 2009, 11:38 | |
| Oui .. je pense que ca devrait être une disjonction de cas ..
Mais ca serait long >.<
Je vais penser à autre chose ..
En tous cas je pense que ca va donner le même résultat c'est que :
xy(x+y)=xz(x+z)=yz(y+z) mais reste à le prouver .. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:09 Jeu 10 Déc 2009, 12:09 | |
| Bon si on part du 1er résultat on aura : (x+y)²(y+z)²(x+z)²=(x²-xy+y²)(x²-xz+z²)(y²-yz+z²) (x+y)² >= 4xy Donc : (x+y)²(y+z)²(x+z)² >= 4^(3) (xyz)^(2) car (x+y)²(y+z)²(x+z)² >= 0 Alors on aura : (x²-xy+y²)(x²-xz+z²)(y²-yz+z²) >= 64(xyz)^(2) et : (x²-xy+y²)(x²-xz+z²)(y²-yz+z²) >=0 Supposons que : x#-y et x#-z et y#-z Alors on aura : 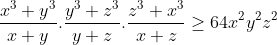 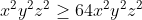 (xyz)²=0 Et on supposant le contraire on aura : x=-y ou x=-z ou y=-z alors (x+y)(x+z)(y+z)=0=xyz On espérons de ne pas faire une autre faute :p | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:12 Jeu 10 Déc 2009, 12:12 | |
| de retour. (j'ai passé ce matin le deuxieme controle et d'habitude mal passé ). pour ce exercice j'ai trouve xyz=0 ou xyz=1. (x3+y3)(y3+z3)(z3+x3)=xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz). si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=0 ==> xyz=0 si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)#0 on a  x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)² on sait que ( x²+y²-xy)(y²+z²-yz)(x²+z²-xz)>= (xyz)². => x=y=z on remplacant dans la premiere equation 2xyz=xyz contradition . donc xyz=0
Dernière édition par marouan777 le Jeu 10 Déc 2009, 12:33, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:17 Jeu 10 Déc 2009, 12:17 | |
| Faux :
(x^(3)+y^(3) ) = (x+y)(x²+y²-xy)
Pas ce que t'a écris ^^ | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:19 Jeu 10 Déc 2009, 12:19 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:22 Jeu 10 Déc 2009, 12:22 | |
| Ah ok ^^
Mais pour le xyz=1
j'aimerais bien que tu me propose des x,y,z ou les 2équations sont vérifiés et que xyz=1 | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:31 Jeu 10 Déc 2009, 12:31 | |
| c pas important de la calculer .
mais comme meme j me suis trompé xyz=1 ne verifie pas .
donc xyz=0 | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:44 Jeu 10 Déc 2009, 12:44 | |
| - marouan777 a écrit:
- de retour. (j'ai passé ce matin le deuxieme controle et d'habitude mal passé ).
pour ce exercice j'ai trouve xyz=0 ou xyz=1.
(x3+y3)(y3+z3)(z3+x3)=xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz).
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=0 ==> xyz=0
si xyz(x²+y²-xy)(y²+z²-yz)(x²+z²-xz)#0
on a  x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)² x²+y²-xy)(y²+z²-yz)(x²+z²-xz)=(xyz)²
on sait que ( x²+y²-xy)(y²+z²-yz)(x²+z²-xz)>= (xyz)².
=> x=y=z on remplacant dans la premiere equation 2xyz=xyz contradition .
donc xyz=0 L'inégalité en rouge est juste seulement quand x,y,z sont positive | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:49 Jeu 10 Déc 2009, 12:49 | |
| Bon je pense que la mienne est correcte donc je pose un exo :p Soit a,b,c>0 MQ: 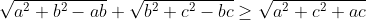
Dernière édition par Sylphaen le Jeu 10 Déc 2009, 14:44, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 12:59 Jeu 10 Déc 2009, 12:59 | |
| Voila ma solution :
on a : (x3+y3)(y3+z3)(z3+x3)= (x+y)3(y+z)3(z+x)3=(xyz)3
dans le cas ou x et y et z sont égal a 0 on aura
0=0 ce qui est juste .
donc dans le cas ou x ou y ou z sont différents de 0 :
c'est faut parce que : P est juste donc non P est fausse
on en conclu que xyz = 0
Sauf erreur bien sûr !!
Dernière édition par darkpseudo le Jeu 10 Déc 2009, 13:14, édité 1 fois | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:11 Jeu 10 Déc 2009, 13:11 | |
| oui c vrai mais je peux dire que (x²+y²-xy)>= (la valeur absolu de xy) comme ça l'inégalité est juste n'est ce pas ?? | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:11 Jeu 10 Déc 2009, 13:11 | |
| Il y'a une erreur ..
Prend x=-y=1 et z=0 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:12 Jeu 10 Déc 2009, 13:12 | |
| Salut :!!
pour cele de VS avez commis des fautes
POur Marouane
pour éliminer (xyz)^3
t a fé (xyz).1/xyz et tu trouve xyz =0 ckyé pas logique !!
pour darkpseudo c une grande faute :!!
don le cas ou x et y ou z sont différents de 0
on ici ou donc u n nombre peut égaler 0 donc xyz peut égaler 0
don 7P né po fausse !!
Bon Jeu !! et bOn olympiade pour les particiapants demain !! | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:15 Jeu 10 Déc 2009, 13:15 | |
| c'est juste une faut d'innatention dans tout les cas ou trouvera xyz=0 c'est ce pas ?? | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:18 Jeu 10 Déc 2009, 13:18 | |
| j'interviens donc ici pour dire qu'aucune solution n'est acceptable(comme a confirmé houssam)....cherchez encore  !!! | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 10 Déc 2009, 13:25 Jeu 10 Déc 2009, 13:25 | |
| je demande le faute dans ma solution .
pour houssam j'ai separé les cas avant d'avancer . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
