Olympiodiose

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:10

Je vais poster un exo pour continuer le jeu :

Problème:

a,b,c des réel postif tel que :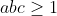
$Olympiodiose - Page 6 Gif$
Montrer que :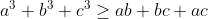
$Olympiodiose - Page 6 Gif$

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:25

Solution :

D'aprés Cheby Chev et I.A.G on a :

d'ou le resultat

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:30

j'étais en train d'écrire ma solution..mais tu étais plus rapide...en tt cas c juste ...même si ce n'est pas bien écris ......propose donc ton exo!!

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:41

probleme :
a,b et c trois nombre réel positive

Mq

$Olympiodiose - Page 6 Gif$

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:46

Elle est facile je laisse la chance pour les autres

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 19:51

aussi

....

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 20:11

yassine-516 a écrit:: En attente de confirmation voila mon problème:
Démontrer que pour tout entier naturel n supérieur ou égal à 3:
$Olympiodiose - Page 6 Gif.latex?\frac{1}{3^3}+\frac{1}{4^3}+....$

Voila la solution ke j'ai trouvé:
Olympiodiose - Page 6 1259525452911

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 20:26

Pour l'inégalité :
(a+b+c)(∑a/(b+c)²)
>(a+b+c)²/3 . ∑(1/(b+c)²)
>(a²+b²+c²). 9/∑(b+c)²
>(a²+b²+c²) . 9 /2(a²+b²+c²)+2(ab+bc+ca)
>(a²+b²+c²) . 9 /4(a²+b²+c²)
>9/4

Sinon ce que tu as fait yassine est correct.

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 20:30

jolie thalés poste ton exo , on attend....

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 20:39

Soit a et b deux réels strictement positifs :
Démontrer que :

(a²+b+3/4)(b²+a+3/4)>(2a+1/2)(2b+1/2)

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:07

solution du problème (sauf erreur):
a²+b+3/4=a²+1/4+b+1/2≥a+b+1/2 (1)
b²+a+3/4=b²+1/4+a+1/2≥a+b+1/2 (2)
en multipliant (1) par (2) on aura :(a²+b+3/4)(b²+a+3/4)≥(a+b+1/2)²
(a+b+1/2)²=a²+b²+2ab+1/4+a+b≥4ab+a+b+1/4=(2a+1/2)(2b+1/2)
CQFD....
avec égalité si a=b=1/2

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:15

poste ton exo,

Sinon j'avais fait pareil sauf pour le passage :

(a+b+1/2)²=1/4(2a+1/2+2b+1/2)²>(2a+1/2)(2b+1/2)

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:29

problème proposé:
je vous propose donc un facile!!!!
soient a b et c des réel positifs qui ont pour somme 1 ...prouver que:
Olympiodiose - Page 6 1259529962151

ENJOY

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:43

deleted

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:48

yassine-516 a écrit:: Voici ma réponse (sauf erreur):
D'apres Schur on a 9abc<=ab+ac+ca (avec a+b+c=1)
donc on doit montrer que 9abc<=2/7+9abc/7 ce qui est facile

dsl mais c faux...application incorrecte de Shur..sinon....tu as prouvé que 9abc<=ab+ac+ca et que 9abc<=2/a+9abc/7.....ça ne veut pas dire que ab+bc+ca=<2/7+9abc/7........

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 21:54

Ah oui c vrai j pas fait attention

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:10

Re (j'ai vu cette exo quelque par il y a des jours ^^)

voila la solution sauf erreur biensur

l'inégalité est equivalent à :
$Olympiodiose - Page 6 Gif$

c'est facile de montrer que

$Olympiodiose - Page 6 Gif$

d'ou le resultat

PS: Majdouline si ma solu est juste merci de poser un probleme à ma place car je n'ai pas pour l'instant.

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:16

9abc/7+2/7
=9/7(1/ab + 1/bc + 1/ca) +2/7 (*)
>(ab+bc+ca)/7 + 2/7
>(ab+bc+ca)/7+6(ab+bc+ca)/7 (**)
>ab+bc+ca

(*) abc(1/ab + 1/bc + 1/ca) = 1 <=> abc=1/(1/ab + 1/bc + 1/ca)
(**) a²+b²+c²>ab+bc+ca <=> (a+b+c)²>3(ab+bc+ca) <=> 1/3>ab+bc+ca <=> 2/7>6(ab+bc+ca)/7

De plus, on peux majorer l'expression ab+bc+ca par un nombre rationnel :
ab+bc+ca
= (ab+bc)/2 + (bc+ca)/2 + (ab+ca)/2
= b(a+c)/2 + c(a+b)/2 + a(b+c)/2
< (a+b+c)²/8 + (a+b+c)²/8 +(a+b+c)²/8 (***)
<3/8

(***) AB<(A+B)²/4

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:26

Autre solution :
Par Shur :
puisque a+b+c=1
Olympiodiose - Page 6 19758aaadfce3afe19aae08a3a632eca662131c7

et

Olympiodiose - Page 6 8ff7c67705b490684d4ce878c009c6b9f3d61d66

on sommant on aura l'inégalité désiré

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:27

puisque just abdess n'a pas de problèmes à poster ...à toi Thalès!!!

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:38

Soit a,b et c des réels positifs strictement tel que a+b+c=1
Démontrer que:

a^3+b^3+c^3>1/2[(a-b)(b-c)+(b-c)(c-a)+(a-b)(c-a)]+3abc

Très facile à faire, j'ai pas de problèmes intéressants ...

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:46

Thalès a écrit:: Soit a,b et c des réels positifs strictement tel que a+b+c=1
Démontrer que:

a^3+b^3+c^3>1/2[(a-b)(b-c)+(b-c)(c-a)+(a-b)(c-a)]+3abc

es tu sur ???
car (a-b)(b-c)+(b-c)(c-a)+(a-b)(c-a)=ab+bc+ca-a²-b²-c²<0
alors 3abc>1/2[(a-b)(b-c)+(b-c)(c-a)+(a-b)(c-a)]+3abc
donc il suffit de démontrer que /sum a³>3abc
ce qui est trivial par Am-Gm
mais on n'a pas utilisé la condition a+b+c=1!!!!!!!!!
(sauf erreur)

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 22:49

Lol , bah je n'avais pas autre chose de plus intéressant,
Perso j'ai pensé à faire ça :
a^3+b^3+c^3-3abc
=1/2(a+b+c) [(a-b)²+(b-c)²+(c-a)²]
=1/2 [(a-b)²+(b-c)²+(c-a)²]
>1/2 [(a-b)(b-c)+(b-c)(c-a)+(a-b)(c-a)]

Sinon ta méthode est juste, probablement il doit y avoir une faute dans l'énoncé puisque la condition a+b+c=1 dans ta démo n'a pa été nécessaire...
Poste un exo

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 23:28

si on continue comme ça ....ça sera un jeu des inégalités...donc changeons de genre Wink

problème proposé:
soit A une partie de IR...tel que : 1£A et x£A=>x²£A et (x-2)²£A=>x£A
montrer que 2004+√(2003) appartient à A
P.S £ =appartient à
ENJOY Wink

Sujet: Re: Olympiodiose Dim 29 Nov 2009, 23:40

on a 1€A <=> (3-2)²€A => 3€A => 9€A
<=> (5-2)²€A => 5€A => 25€A
<=>(7-2)²€A => 7€A => 49€A etc...
jusqu'à ce qu'on trouve 2003€A <=> ((2+V2003)-2)²€A => 2+V2003€A <=> (2+V2003)²€A <=> (4+V2003-2)²€ A => 4+V2003€A
jusqu'à ce qu'on arrive à 2004+V2003 € A