| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:20 Mar 01 Déc 2009, 13:20 | |
| oui samix je m'en suis rendu compte avant de lire ton message...je me suis un peu precipitée.. | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:21 Mar 01 Déc 2009, 13:21 | |
| - soukki a écrit:
- oui samix je m'en suis rendu compte avant de lire ton message...je me suis un peu precipitée..
Bah oué parce que tu as eu la possibilité de supprimer ton message au lieu de l'éditer xD | |
|
  | |
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:23 Mar 01 Déc 2009, 13:23 | |
| | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:28 Mar 01 Déc 2009, 13:28 | |
| je poste donc ma solution.... solution du problème(sauf erreur):j'essayerai de n'appliquer aucun théorème  on a (x-y)(y-z)(z-x)≤0 <=>x²y+y²x+z²x≥x²z+y²x+z²y (1) en divisant (1) par x on aura:  en divisant (1) par y on aura:  en divisant (1) par z on aura:  en sommant ces trois inégalités on obtient le résultat suivant:      | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:38 Mar 01 Déc 2009, 13:38 | |
| Bien joué, sauf une petite erreur de frappe dans la ligne qui suit "en sommant les trois inégalités", à la fin on a z².y/x xD | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 | |
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:40 Mar 01 Déc 2009, 13:40 | |
| majdouline tu etais plus vite que moi , la meme solution bravo^^
poste un exo.. | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 13:46 Mar 01 Déc 2009, 13:46 | |
| Perso j'avais supposé que : x².y/z+y².z/x+z².x/y<x²+y²+z²
x².z/y+y².x/z+z².y/x<x².y/z+y².z/x+z².x/y
=> (x².z/y+y².x/z+z².y/z)(x².y/z+y².z/x+z².x/y)<(x²+y²+z²)²
(contradiction d'après C.S)
Finalement c'est la même méthode... | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:24 Mar 01 Déc 2009, 14:24 | |
| Majdouline on attend ton exo xD | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:29 Mar 01 Déc 2009, 14:29 | |
| mais je crois que c'est à ayoub xD.... | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:31 Mar 01 Déc 2009, 14:31 | |
| bSr ! Alors Pour Que le jeux continue, je propose cette Serie d'exos selectioné de ma part : Probléme Proposé : P.S : La Solution doit étre Compléte. A++ !  | |
|
  | |
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:47 Mar 01 Déc 2009, 14:47 | |
| personne n'osera faire tous ces exos a la fois ce deviendra ennuyeux...choisi un seul exo si tu veux...!! | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:54 Mar 01 Déc 2009, 14:54 | |
| Oui, comme si c'était un devoir d'olympiade qu'on fait normalement en 3h... | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 14:58 Mar 01 Déc 2009, 14:58 | |
| - Thalès a écrit:
- Oui, comme si c'était un devoir d'olympiade qu'on fait normalement en 3h...
Pas de Probléme Prenait Votre Temps ! Meme un 1/2 jour ...  | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 15:01 Mar 01 Déc 2009, 15:01 | |
| - soukki a écrit:
- personne n'osera faire tous ces exos a la fois ce deviendra ennuyeux...choisi un seul exo si tu veux...!!
Comme Vous voulez ! Alors la Solution de 2 Exos est Suffisante ... !  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:00 Mar 01 Déc 2009, 16:00 | |
| solutions de deux exos(sauf erreurs):je poste donc la solution du deuxieme et du dernier exo: solution du dernier exo:par l'inégalité de Cauchy-Schwartz on a : ^2+(x^2+1))(x(x+1)+1)}\geq%20\sqrt{x(x+1)^3}+\sqrt{x^2+1}) (x^2+x+1)}\geq%20\sqrt{x(x+1)^3}+\sqrt{x^2+1}) \geq%20\sqrt{2}(\sqrt{x(x+1)^3}+\sqrt{x^2+1})) donc il suffit de demontrer que : 3(x²+1)≥2(x²+x+1)<=>(x-1)²≥0 ce qui est tjs vrai CQFD..... ------------------------------------------------------------------------- solution du deuxième exo:posons: =a_{n}x^n+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}) (a_{n}(2x)^n+a_{n-1}(2x)^{n-1}+...+a_{1}(2x)+a_{0})=16(x-1)(a_{n}x^n+a_{n-1}x^{n-1}+...+a_{1}x+a_{0})) donc le deugrés de celle à gauche et le meme de celle à droite alors  =>n=4 alors p(x)=a(x-x1)(x-x2)(x-x3)(x-x4) or on a p(2)=0 (en remplaçant x par 1 et p(16)=0 en remplaçant x par 16 donc p(x)=a(x-2)(x-16)(x-x3)(x-x4) apres un petit calcul on trouve que x3=8 et x4=4 d'où p(x)=a(x-2)(x-16)(x-8 )(x-4) avec a un coefficient reel | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:06 Mar 01 Déc 2009, 16:06 | |
| Pour l'exo 1 j'ai trouvé 4 solutions :
V(x+2)=(-1+V13)/2 ou (1+V13)/2 ou (-V2+V14)/2 ou
(V2 + V14)/2
je suis sûr a 99% que c'est faux ... Mais bon mieu vaut essayer et se tromper que pas essayer du tt | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:12 Mar 01 Déc 2009, 16:12 | |
| Pour l'exo 1 :
on doit résoudre l'équation dans [V3,+00[
en levant au carré :
x^6-6x^4++9x²-x-2=0
(x-2)(x^5+2x^4-2x^3-4x²+x+1)=0
(x-2)(x²+x-1)(x^3+x²-2x-1)=0
pour la 3eme équation j'aarive pas a factoriser j'ai pensé a methode de cadran mais c'est long | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:14 Mar 01 Déc 2009, 16:14 | |
| j'attends tjs une confirmation.... | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:20 Mar 01 Déc 2009, 16:20 | |
| Oui Bravo Majdouline, a Toi de poster ... P.S : Pour les intéressés aux autres Exos, un MP est Mieux !  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:56 Mar 01 Déc 2009, 16:56 | |
| problème proposé:a,b,c>0 et  et  et  montrer que: xy+yz+zx≥2(x+y+z)have fun montrer que: xy+yz+zx≥2(x+y+z)have fun  | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 16:59 Mar 01 Déc 2009, 16:59 | |
| - samix a écrit:
- Pour l'exo 1 :
on doit résoudre l'équation dans [V3,+00[
en levant au carré :
x^6-6x^4++9x²-x-2=0
(x-2)(x^5+2x^4-2x^3-4x²+x+1)=0
(x-2)(x²+x-1)(x^3+x²-2x-1)=0
pour la 3eme équation j'aarive pas a factoriser j'ai pensé a methode de cadran mais c'est long Je ne vois pas pourquoi tu veux absolument factoriser l'expression... Si ce que tu as fait est juste, cela veux dire que x=2 ou x²+x-1=0(facile à résoudre) ou x^3+x²-2x-1=0 chose qui ne doit pas te poser problème : Si tu considère la fonction f(x)=x^3+x²-2x-1, elle est croissante sur [V3;+oo[, donc x>V3 => f(x)>f(V3) où f(V3) est positif strictement, donc f(x) sera toujours positive strictement et ne pourra jamais être égale à 0 sur l'intervalle [V3;+oo[ | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 01 Déc 2009, 17:20 Mar 01 Déc 2009, 17:20 | |
| Pour ma part j'ai pas essayé de factorisé , à la fin j'suis sur : 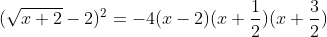 Mais j'ai pas terminé ..  | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 02 Déc 2009, 18:12 Mer 02 Déc 2009, 18:12 | |
| Majdouline poste la soluce de ton problème pour continuer ... | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 02 Déc 2009, 20:34 Mer 02 Déc 2009, 20:34 | |
| bonsoir.... les 48h ne se sont pas encore écoulées...réessayez d'avantage ...croyez moi il existe une solution en 3 lignes (c simple)  ....sinon...je poste la solution maintenant.....choisissez!!!!.....j'attends vos réponses!!!! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
