| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 26 Nov 2009, 22:36 Jeu 26 Nov 2009, 22:36 | |
| c'est evident je pense.
ya rien a demontrer. | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 26 Nov 2009, 22:37 Jeu 26 Nov 2009, 22:37 | |
| okey probleme 4:a0 , a1 , a2 ,......., a1998 sont les coefficients du polynome=(1+x+x^{2})^{999}) montrez que la somme a0+a2+a4+.........+a1998 est un entier pair montrez que la somme a0+a2+a4+.........+a1998 est un entier pair | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 26 Nov 2009, 23:32 Jeu 26 Nov 2009, 23:32 | |
| f(x)=a0+a1x+a2x²+...+a1998x^1998
f(1)=a0+a1+a2+...+a1998
f(1)=(1+1+1)^999=3^999
Donc a0+a1+a2+...+a1998=3^999 (a)
f(-1)=a0-a1+a2-a3+...+a1998
f(-1)=(1-1+1)^999=1
Donc a0-a1+a2-a3+...+a1998 =1 (b)
En sommant (a) et (b) on aura : 2S=3^999-1
S=3^999/2 (tel que S=a0+a2+...+a1998)
3=4k-1 (k=1)
3^999=4k'-1 (tel que k'€N)
3^999+1=4k'
S=2k'
S est donc pair | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 08:42 Ven 27 Nov 2009, 08:42 | |
| jolie thalés poste ton probleme | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 12:26 Ven 27 Nov 2009, 12:26 | |
| - Thalès a écrit:
- f(x)=a0+a1x+a2x²+...+a1998x^1998
f(1)=a0+a1+a2+...+a1998
f(1)=(1+1+1)^999=3^999
Donc a0+a1+a2+...+a1998=3^999 (a)
f(-1)=a0-a1+a2-a3+...+a1998
f(-1)=(1-1+1)^999=1
Donc a0-a1+a2-a3+...+a1998 =1 (b)
En sommant (a) et (b) on aura : 2S=3^999-1
S=3^999/2 (tel que S=a0+a2+...+a1998)
3=4k-1 (k=1)
3^999=4k'-1 (tel que k'€N)
3^999+1=4k'
S=2k'
S est donc pair pas toujours par exemple 9. f(1)=3^999 donc la somme est impair | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 14:14 Ven 27 Nov 2009, 14:14 | |
| - marouan777 a écrit:
- Thalès a écrit:
- f(x)=a0+a1x+a2x²+...+a1998x^1998
f(1)=a0+a1+a2+...+a1998
f(1)=(1+1+1)^999=3^999
Donc a0+a1+a2+...+a1998=3^999 (a)
f(-1)=a0-a1+a2-a3+...+a1998
f(-1)=(1-1+1)^999=1
Donc a0-a1+a2-a3+...+a1998 =1 (b)
En sommant (a) et (b) on aura : 2S=3^999-1
S=3^999/2 (tel que S=a0+a2+...+a1998)
3=4k-1 (k=1)
3^999=4k'-1 (tel que k'€N)
3^999+1=4k'
S=2k'
S est donc pair
pas toujours par exemple 9.
f(1)=3^999 donc la somme est impair En effet tu a raison et : 3^n quelque soit n un nombre impair = 4k -1 donc 3^999 = 4k-1 et non +1 donc ce que thalés a dit est juste... le probléme c'est pourquoi il a trouver que la même somme egal a 3^999 et a 1 c'est pas logique
Dernière édition par darkpseudo le Ven 27 Nov 2009, 15:20, édité 2 fois | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 14:34 Ven 27 Nov 2009, 14:34 | |
| aussii non.
le nombre 3^n =4k+1 ou 4k+3 . | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 14:52 Ven 27 Nov 2009, 14:52 | |
| leul ... regarde
si 3^n = 4k+3 c'est que 3^n= 4c-1 avec c=k+1
maintenant on revient au faite que
3^n= 4k+1 ou 4k-1
mais tant que n est un nombre impaire alrs :
3^n=4k-1 tu as compris ?? | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 15:07 Ven 27 Nov 2009, 15:07 | |
| ah oui dsl j'ai pas pris attention de ton enoncé" ...n est impair"
d'ailleurs c pas notre probleme maintenent,puisque on sait que l somme est impaire.quelque chose ça va pas dans l'exerc | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 | |
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 15:22 Ven 27 Nov 2009, 15:22 | |
| oé sa je le savait ... Mais ce que je n'arrive pas a comprendre c'est pourquoi il a fait
S=3^999 puis S=1
et 2S = 3^999 - 1
j'ai pas compris cette partie de l'exercice | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 15:32 Ven 27 Nov 2009, 15:32 | |
| exercice fausse.quelqu'un peut poster un exercice pour avancer . | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 15:40 Ven 27 Nov 2009, 15:40 | |
| Voila je poste un exo : on a f dala mou3arafa de R jusqu'a R tel que: 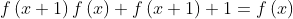 bayne ana dala dawrya mou7adidan dawraha ... | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 17:00 Ven 27 Nov 2009, 17:00 | |
| Salut
l'exercice et la solution sont totalement vraix, je ne sais pas ou vous voyez la faute , en plus moi j'ai demandé de montrez que la somme a0+a2+a4+.....+a1998 est un entier pair et non pas f(1)=a0+a1+a2+....+a1998=3^999 | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 17:04 Ven 27 Nov 2009, 17:04 | |
| | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 17:41 Ven 27 Nov 2009, 17:41 | |
| Re
pour mon exo , si quelqu'un poureez nous repondre si cette chose est juste
il existe k bihayte 3=4k-1 (k=1)
donc il existe k'' bihaytou 3^(999)=4k"-1
si cette chose est vraix donc l'exo est correcte, (et je ne pense pas qu'il est faux car je l'ai pris d'un olympiade)
on attendant la réponse, samix poste l'exo prochaine
Dernière édition par just-abdess le Ven 27 Nov 2009, 17:57, édité 1 fois | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 17:56 Ven 27 Nov 2009, 17:56 | |
| Probleme:
Sois ABC un triangle et M un point de [BC], la droite parallèle à (AM) et qui passe par B coupe (AC) en N , et la droite parallèle à (AM) et qui passe par c coupe (AB) en P.
Montrer que : 1/AM=1/BN + 1/CP | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 | |
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 | |
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:00 Ven 27 Nov 2009, 19:00 | |
| bonsoir  | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:13 Ven 27 Nov 2009, 19:13 | |
|
Dernière édition par darkpseudo le Ven 27 Nov 2009, 20:29, édité 2 fois | |
|
  | |
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:26 Ven 27 Nov 2009, 19:26 | |
| (1) on pose
m=(x-3)/(x+1) on obtient
f(m)+f((m-3)/(1+m))=(3+m)/(1-m)
(2) on pose
m=(x+3)/(1-x) on obtient
f((3+m)/(1-m))+f(m)=(m-3)/(1+m)
on sommant 1 et 2
2f(m)+f((m-3)/(1+m))+f((3+m)/(1-m))=8m/(1-m^2)
toukafi2
2f(m)+m=8m/(1-m^2)
f(m)=4m/(1-m^2)-m/2 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:36 Ven 27 Nov 2009, 19:36 | |
|
Dernière édition par darkpseudo le Ven 27 Nov 2009, 20:29, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:40 Ven 27 Nov 2009, 19:40 | |
| bon voilà de retour^^....
dsl pour mon intervention....la solution de darkpseudo est fausse.....celle de souki est correcte...(sauf erreur)...à toi soukki!!!! | |
|
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 27 Nov 2009, 19:45 Ven 27 Nov 2009, 19:45 | |
| - majdouline a écrit:
- bon voilà de retour^^....
dsl pour mon intervention....la solution de darkpseudo est fausse.....celle de souki est correcte...(sauf erreur)...à toi soukki!!!! meme avis majdouline a toi la main soukki | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
