| | Inégalité triangulaire |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Inégalité triangulaire Sujet: Inégalité triangulaire  Ven 01 Jan 2010, 17:21 Ven 01 Jan 2010, 17:21 | |
| a,b,c les mesures des cotés d'un triangle.
montrez que (a+b+c)^2>4(a^2+b^2).
sachant que a<b<c .
Dernière édition par nmo le Sam 02 Jan 2010, 15:08, édité 3 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Ven 01 Jan 2010, 20:34 Ven 01 Jan 2010, 20:34 | |
| contre exemple: a=7,b=5,c=3 ??????
sauf erreur.... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 15:06 Sam 02 Jan 2010, 15:06 | |
| J'ai oublié de dire que a<b<c | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 15:23 Sam 02 Jan 2010, 15:23 | |
| - nmo a écrit:
- J'ai oublié de dire que a<b<c
L'inégalité étant symétrique, l'ordre des variables n'y change pratiquement rien. Le contre exemple de majdouline demeure donc efficient. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 15:49 Sam 02 Jan 2010, 15:49 | |
| Si tu prends c=5 b=4 a=3.
Tu vas trouver que c'est vrai. | |
|
  | |
mehdibouayad20
Expert sup

 Nombre de messages : 1702 Nombre de messages : 1702
Age : 33
Localisation : Fez City
Date d'inscription : 15/12/2007
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 16:43 Sam 02 Jan 2010, 16:43 | |
| même si .. je dit que le contre exemple reste vrai ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 16:51 Sam 02 Jan 2010, 16:51 | |
| - mehdibouayad20 a écrit:
- même si .. je dit que le contre exemple reste vrai !
Donne moi un autre contre exemple qui vérifie les nouveaux conditions. Sinon c'est vrai. | |
|
  | |
mehdibouayad20
Expert sup

 Nombre de messages : 1702 Nombre de messages : 1702
Age : 33
Localisation : Fez City
Date d'inscription : 15/12/2007
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 02 Jan 2010, 17:48 Sam 02 Jan 2010, 17:48 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Dim 03 Jan 2010, 09:35 Dim 03 Jan 2010, 09:35 | |
| - mehdibouayad20 a écrit:
- a=8 ;b=5 ;c=3
Ce n'est pas un triangle. Pour que ce soit un triangle il faut que a<b+c. Pour ton exemple a=8 et b+c=8. Donc les points sont allignés et ne forment pas ainsi un triangle. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Dim 03 Jan 2010, 13:15 Dim 03 Jan 2010, 13:15 | |
| puisque a<b<c :
(a+b+c)>3/2(a+b)
(a+b+c)^2 >9/4(a+b)^2>4(a^2+b^2)
sauf erreur !! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Dim 03 Jan 2010, 13:51 Dim 03 Jan 2010, 13:51 | |
| Nous avions déjà signalé que ce problème n'était pas correct, et majdouline a proposé un contre-exemple pour consolider son affirmation : 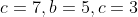 Ensuite, pour darkpseudo, - darkpseudo a écrit:
(a+b+c)^2 >9/4(a+b)^2>4(a^2+b^2)
Comment tu expliques ce dernier passage ?
Dernière édition par Dijkschneier le Dim 03 Jan 2010, 15:26, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Dim 03 Jan 2010, 15:18 Dim 03 Jan 2010, 15:18 | |
| - Dijkschneier a écrit:
- Nous avions déjà signalé que ce problème n'était pas correct, et majdouline a proposé un contre-exemple pour prouver cela :
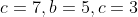
Ensuite, pour darkpseudo,
- darkpseudo a écrit:
(a+b+c)^2 >9/4(a+b)^2>4(a^2+b^2)
Comment tu expliques ce dernier passage ? Oui il faut démontrer ce qui est en rouge. Ensuite l'inégalité est juste. | |
|
  | |
{}{}=l'infini
Expert sup

 Nombre de messages : 1164 Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  Sam 09 Jan 2010, 20:36 Sam 09 Jan 2010, 20:36 | |
| } signifie supérier à
(a+b+c)^2 = a^2 +b^2 +c^2 +2ab+2ac+2bc
} a^2 + b^2 + b^2 + 2a^2 + 2a^2 + 2b^2
donc : (a+b+c)^2 } 4b^2 + 5a^2
sauf erreur.
le fait que a,b et c sont des cotes d'un triangle n'est pas nécessaire
et pour le contre exemple de "mehdibouayad20" n'est pas accepté car a sup à b sup à c. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Inégalité triangulaire Sujet: Re: Inégalité triangulaire  | |
| |
|
  | |
| | Inégalité triangulaire |  |
|
