easy but nice...

a,b,c>0...
prouvez que:

donc supposons que a+b+c=1(homogénéité)
l'inégalité est équivalente à: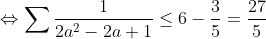



prouvons que :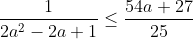

cela équivaut à :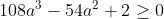

remarquons que 1/3 est une double racine et hop!!on obtient la factorisation:

ce qui est vrai...on a donc: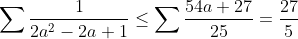

CQFD.....

oui c ca^^...j'ai fé la meme preuve.

majdouline a écrit:

or :

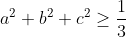
alors:

En passant de 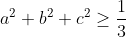à , le signe devrait s'inverser.

bien vu Dijkschneier

En effet, d'après ta solution Majdouline il suffit de prouver que : 1/1+2(a²+b²+c²)>3/5
<=> 1/3 > a²+b²+c² (alors que c totalement le contraire qui est vrai)
Donc il faut procéder autrement.

Sinon je pense que c'est faisable aisément en utilisant Jensen en considérant la fonction : f(x)=(1-2x)²/(1+2x²-2x) :
f(a)+f(b)+f(c)>= 3 f((a+b+c)/3)= 3/5

oui c'est la celebre inegalité du japon 97, by the way je vous propose une inegalité assez facile:

prouver que pour chaque quadrilatère avec des cotes a,b,c,d

a²+b²+c² > d²/3

3(a²+b²+c²)>= (a+b+c)², et on aura forcément d<a+b+c d'où le résultat

re^^...voilà je viens de corriger...voir mon récent message

Thalès a écrit:

et on aura forcément d<a+b+c

Pourquoi ?

Dijkschneier a écrit:

Thalès a écrit:

et on aura forcément d<a+b+c

Pourquoi ?

il est évident que dans chaque quadrilatère on a: a+b+c>d càd (a+b+d)²>d² ==> 3(a²+b²+c²)>d²
cqfd

Dijkschneier a écrit:

Thalès a écrit:

et on aura forcément d<a+b+c

Pourquoi ?

C'est très élémentaire et facile à prouver à partir de l'inégalité triangulaire :
Prends ABCD un quadrilatère et pose : a=AB ; b=AD ; c=BC ; d=DC
et pose aussi : BD=K
Dans le triangle ABD : a+b>K => a+b+c>K+c
Dans le triangle BCD : K+c>d
donc a+b+c>d

majdouline a écrit:

prouvons que :

cela équivaut à :

C'est plutôt -54
Sinon jolie la solution !

Thalès a écrit:

C'est très élémentaire et facile à prouver à partir de l'inégalité triangulaire :
Prends ABCD un quadrilatère et pose : a=AB ; b=AD ; c=BC ; d=DC
et pose aussi : BD=K
Dans le triangle ABD : a+b>K => a+b+c>K+c
Dans le triangle BCD : K+c>d
donc a+b+c>d

Merci bien !

Thalès a écrit:

Sinon je pense que c'est faisable aisément en utilisant Jensen en considérant la fonction : f(x)=(1-2x)²/(1+2x²-2x) :
f(a)+f(b)+f(c)>= 3 f((a+b+c)/3)= 3/5

bonsoir c'est le lien de Majdouline dans le JOPSM qui m'a ramené ici
juste pour corriger f(x) n'est pas convexe sur [0,1]!

Oui pourque ça soit une contradiction il faut que les trois variables a,b et c soient dans l'intervalle : [1/2-V3/6;1/2+V3/6] (sauf erreur d'après la seconde dérivée)

Bonsoir
sa se voit que la fonction n'est pas convexe essaye de tracer sa dérivée dans un logiciel pour comprendre
en + on aura jamais une contradiction car on a déja une condition sinn toutes les inégalités seront résolus par JENSEN

imanos a écrit:

Bonsoir
sa se voit que la fonction n'est pas convexe essaye de tracer sa dérivée dans un logiciel pour comprendre
en + on aura jamais une contradiction car on a déja une condition sinn toutes les inégalités seront résolus par JENSEN

Non cette fonction est convexe ( Sans penser à sa seconde dérivée )

On a f(0)=1 , f(1/2)=0 et f(1)=1
Juste imagine sa courbe représentative puisque f est dérivable ( donc continue ) sur [0,1].