tarask
Expert sup
 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 | | Sujet: inégalité un peu compliquée Jeu 17 Juin 2010, 22:39 | |
| soient x et y deux réels strictement positifs tels que x+y=8
Demontrez que (x+1/y)^2 + (y+1/x)^2 ≥ 289/8 | |
|
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: inégalité un peu compliquée Jeu 17 Juin 2010, 23:16 | |
| D'après Cauchy-Schwarz: ((x + \frac{1}{y})² + (y + \frac{1}{x})²) \geq (x+y + \frac{x+y}{xy})² = (8 + \frac{8}{xy})² \geq (8 + \frac{8}{16})) (sachant que ² \geq 4xy) donc 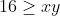 ) Donc : ² + (y + \frac{1}{x})² \geq \frac{1}{2}(8 + \frac{1}{2})² = \frac{289}{8}) CQFD PS : C'est faisable avec Chebyshev, une fonction en sachant que y = 8-x, Jensen, Moyenne généralisée, ... bref, faut juste chercher, c'est du déjà-vu. | |
|
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: inégalité un peu compliquée Ven 18 Juin 2010, 09:45 | |
| dsl mais chui nouveau sur lforum c pour ça que j'ai po fait attention ! en tt cas merci oussama ! | |
|
Contenu sponsorisé
| | Sujet: Re: inégalité un peu compliquée | |
| |
|
