| | Une limite bien compliquée .. T.T |  |
|
+7W.Elluizi MohE medamine. nami.ne Bison_Fûté soumitous Esperanza 11 participants |
|
| Auteur | Message |
|---|
Esperanza
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 30
Localisation : rabat
Date d'inscription : 28/01/2011
 |  Sujet: Une limite bien compliquée .. T.T Sujet: Une limite bien compliquée .. T.T  Ven 28 Jan 2011, 21:17 Ven 28 Jan 2011, 21:17 | |
|
Dernière édition par Esperanza le Mer 28 Sep 2011, 23:19, édité 2 fois | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Ven 28 Jan 2011, 21:46 Ven 28 Jan 2011, 21:46 | |
| X^2007-2007X+2006 = (X^2007 - x) - 2006(x-1) X^2007-x = x(x^2006 - 1) = x(x-1)(sigma de k=0 à 2005 x^k) (voir la factorisation de a^n-b^n) Donc X^2007-x = (x-1)(sigma de k=1 à 2006 x^k) D'où X^2007-2007X+2006 = (x-1)(sigma de k=1 à 2006 x^k - 2006) Lim : ( X^2007-2007X+2006 ) / ( X-1)² quand X tend vers 1 = Lim : ( sigma de k=1 à 2006 x^k - 2006 ) / ( X-1) quand X tend vers 1 On a sigma de k=1 à 2006 x^k - 2006 = x^2006 + x^2005 + x^2004....+x-2006 =x^2006-1 + x^2005-1 + x^2004-1+.....+x-1 =(x-1)(sigma de k=0 à 2006 x^k) + (x-1)(sigma de k=0 à 2005 x^k) + ....+(x-1) =(x-1) ( sigma de k=0 à 2006 x^k + sigma de k=0 à 2005 x^k + .... +1) Lim : ( sigma de k=1 à 2006 x^k - 2006 ) / ( X-1) quand X tend vers 1 =Lim : (x-1) ( sigma de k=0 à 2006 x^k + sigma de k=0 à 2005 x^k + .... +1) / ( X-1) quand X tend vers 1 =Lim  sigma de k=0 à 2006 x^k + sigma de k=0 à 2005 x^k + .... +1) quand X tend vers 1 = sigma de k=0 à 2006 1^k + ..... +1 =(1/2)2006.2007 Sauf erreur (J'ai édité une faute le résultat n'est pas 2007)
Dernière édition par soumitous le Dim 30 Jan 2011, 22:49, édité 1 fois | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 10:08 Sam 29 Jan 2011, 10:08 | |
| - Esperanza a écrit:
- Salaam les matheux ..

Xwéé vraiment et sincérement besoin de vous a fin de résoudre cette limite d' enfer .. !!
Harast m3ahaa rassi mais en vain .. T.T
Lim : ( X^2007-2007X+2006 ) / ( X-1)²
quand X tend vers 1 BJR à Vous !! @ soumitous !!! Je ne comprends pas ta Transformation ! C'est un peu maladroit .... Il me semble plus judicieux d'écrire : X^2007-2007X+2006 ={X^2007 - 1} - 2007.{X-1} d'utiliser en suite La Formule du Binôme de NEWTON pour s'occuper de l'expression {X^2007 - 1} en l'écrivant sous la forme (X-1).{1+X+X^2+ ......... + X^2006} lever une fois l'indétermination .... Celà vous amènera à chercher la limite quand X ------> 1 de l'expression : {-2006+X+X^2+ ....... + X^2006}/(X-1) enfin , penser à une DERIVEE pour CONCLURE ......... Bonne Journée !! | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 12:58 Sam 29 Jan 2011, 12:58 | |
| Je n'ai pas encore étudié la dérivée... je vais réécrire ma réponse en Latex espérant qu'elle sera plus claire | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 | |
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 14:14 Sam 29 Jan 2011, 14:14 | |
| BJR Soumitous !!!
J'ai deux observations à faire :
1) C'est , et celà a été mon Job pendant des années , Mon Devoir de lire tout ... Il est vrai que tu y arrives sans utiliser la DERIVATION ....
Cependant ton résultat final ( dernière Ligne ) est Faux !!
On devrait trouver comme LIMITE
1+2+3+ ....... + 2006=(1/2).2006.2007=1003.2007= .....
2) Je pense que des camarades à Toi en 1BACSM sont arrivés au
Chapitre de la DERIVATION et de l'Etude des Variations etc ......
Donc on pourrait retrouver ton résultat en exploitant la DERIVATION comme je l'ai indiqué dans Mon Post au dessus .
Bonne Chance et Bravo pour Ton Travail !!! LHASSANE
Dernière édition par Bison_Fûté le Sam 29 Jan 2011, 15:06, édité 1 fois | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 14:42 Sam 29 Jan 2011, 14:42 | |
| J'ai complètement disjoncté à la fin veuillez excuser mon erreur fatale xD
Je ne nie pas qu'il y a d'autres méthodes mais vu les leçons qu'on a étudié je me vois obligé d'utiliser cette méthode. Et on est un peu en retard par rapport au programme alors....
Merci pour votre aide | |
|
  | |
Esperanza
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 30
Localisation : rabat
Date d'inscription : 28/01/2011
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 15:52 Sam 29 Jan 2011, 15:52 | |
|
Dernière édition par Esperanza le Mer 28 Sep 2011, 23:19, édité 1 fois | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 17:32 Sam 29 Jan 2011, 17:32 | |
| De rien ^^
J'ai juste remplacer le x par 1 c'est pour cela que j'ai enlevé la limite aussi et comme la dit Bison_Futé le résultat est incorrect:
sigma de k=0 à 2006 1^k +...+1 =1+2+3+ ....... + 2007
=(1/2).2007.2008(somme d'une suite arithmétique)
=1004*2007
=2015028 et non pas 2007
En cas d'erreur corrigez moi SVP | |
|
  | |
nami.ne
Maître

 Nombre de messages : 118 Nombre de messages : 118
Age : 30
Date d'inscription : 05/10/2010
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 17:43 Sam 29 Jan 2011, 17:43 | |
| je m'excuse mais est ce qu'on peut pas calculer le limites de son plus grand degré .... ou ça marche pas ici ?? faut-il supprimer tout d'abord la forme indéterminé 0/0 dsl mais je pose ces questions parce qu'on a pas vraiment entamer la leçon  j'attend vos réponses  | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 17:54 Sam 29 Jan 2011, 17:54 | |
| Pour utiliser la méthode du plus grand degrés il faut que x tant vers + ou - l'infinie ce qui n'est pas le cas
Quand x tant vers un x0 en général on remplace mais vue qu'on a une forme indéterminée (0/0 et d'autres formes regarde dans ton manuel) on a recours à la factorisation par x-x0 (on peut utiliser lmourafi9 ou factoriser par x ou....cela dépend de la limite) | |
|
  | |
nami.ne
Maître

 Nombre de messages : 118 Nombre de messages : 118
Age : 30
Date d'inscription : 05/10/2010
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 18:00 Sam 29 Jan 2011, 18:00 | |
| je te remerci ( soumitous ) pour l'explication  | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 18:01 Sam 29 Jan 2011, 18:01 | |
| | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 18:09 Sam 29 Jan 2011, 18:09 | |
| - soumitous a écrit:
- De rien ^^
J'ai juste remplacer le x par 1 c'est pour cela que j'ai enlevé la limite aussi et comme la dit Bison_Futé le résultat est incorrect:
sigma de k=0 à 2006 1^k +...+1 =1+2+3+ ....... + 2007
=(1/2).2007.2008(somme d'une suite arithmétique)
=1004*2007
=2015028 et non pas 2007
En cas d'erreur corrigez moi SVP OUI , Il y a ERREUR ... et je l'ai déjà dit plus HAUT .... << Cependant ton résultat final ( dernière Ligne ) est Faux !! On devrait trouver comme LIMITE 1+2+3+ ....... + 2006=(1/2).2006.2007=1003.2007= ..... >> | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 18:19 Sam 29 Jan 2011, 18:19 | |
| Euh sigma de k=0 à 2006 1^k c'est pas égal à 2007? | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 18:51 Sam 29 Jan 2011, 18:51 | |
| - soumitous a écrit:

Sauf erreur Revois Ta Réponse ci-dessus ( la dernière Ligne ) ! C'est le mieux pour Toi !!! | |
|
  | |
Esperanza
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 30
Localisation : rabat
Date d'inscription : 28/01/2011
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 19:45 Sam 29 Jan 2011, 19:45 | |
| .. 
Dernière édition par Esperanza le Mer 28 Sep 2011, 23:20, édité 1 fois | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Sam 29 Jan 2011, 19:52 Sam 29 Jan 2011, 19:52 | |
| - Esperanza a écrit:
- C'est le mieux pour Toi !!!
je sens que cette phrase est HORS SUJET .. -.-'
Elle sait et elle a dit qu'elle a commis une faute .. et j' apprécie vraiment son effort et son intelligence ( Tbark Allah  ) )
Monsieur Bison_Fûté si la faute est claire pour vous .. je vous demande de la préciser SVP ..  Je suis DSL mais Soumitous l'a reconnue déjà .... << C'est le mieux pour Toi >> veut dire éthymologiquement : ce sera d'un grand intérêt pour Toi de revoir tes écritures ... Celà n'a rien de méchant , ni péjoratif et Je sais ce que Je dis . Donc inutile de revenir là dessus !! Enfin Soyons Cool , on n'est pas dans une salle de Classe !!! | |
|
  | |
medamine.
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 29
Date d'inscription : 18/10/2010
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Dim 30 Jan 2011, 21:25 Dim 30 Jan 2011, 21:25 | |
| lmohim la réponse serait 4020022 donc Où est l'erreur !
pr X^2006+X^2005+..................+X+1-2006 =X^2005+2X^2004+3X^2003+........+2005X+2006+1
= (pr X=1) 4020022 | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Dim 30 Jan 2011, 21:40 Dim 30 Jan 2011, 21:40 | |
| - medamine. a écrit:
- lmohim la réponse serait 4020022 donc Où est l'erreur !
pr X^2006+X^2005+..................+X+1-2006 =X^2005+2X^2004+3X^2003+........+2005X+2006+1
= (pr X=1) 4020022 Je ne comprends pas tout cet acharnement totalement inapproprié ! L'erreur , c'est tout simple 2007 ce n'est pas la même chose que (1/2).2006.2007=2013021 C'est tout simple et celà , Soumitous l'a compris !! Pourquoi est ce que vous intervenez pour RIEN !!! Arrêtons ces prises de bec !!! PS : Je ne vois d'ou tu sors le 4020022 ????? | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Dim 30 Jan 2011, 23:29 Dim 30 Jan 2011, 23:29 | |
| Bonsoir!
Si je ne me trompe pas, on peut à partir du cinquième ligne de la solution de soumitous, considérer la fonction g(x)=sum_{k=1}^{2006}x^k, et utiliser la dérivé, ce peut-etre plus simple puisque g(1)=2006. | |
|
  | |
medamine.
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 29
Date d'inscription : 18/10/2010
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Lun 31 Jan 2011, 02:26 Lun 31 Jan 2011, 02:26 | |
| Bah je n'interviens pas pour rien mais le 4020021 était un résultat d'une petite faute de calcule j'ai mis un 2003 au lieu du 1003 c tout et merci pour votre correction MR.Bison_Fûté mais aussi je n'ai pas apprécié votre façon de poster le commentaire .... Et merci encore une fois pour votre correction !! | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Lun 31 Jan 2011, 12:28 Lun 31 Jan 2011, 12:28 | |
| Soyons un peu raisonnable,la Limite de cette fonction (et comme l'a déjà signalé Mr.Lhassane) est : 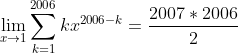 | |
|
  | |
steve 94
Féru

 Nombre de messages : 60 Nombre de messages : 60
Age : 31
Localisation : RABAT
Date d'inscription : 18/01/2011
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Lun 31 Jan 2011, 15:22 Lun 31 Jan 2011, 15:22 | |
| slt , je pense que j'ai pitetre trouver une soluce ,mais ca concorde avec ce qui a été dit auparavant :
on X^2007-2007x+2006=1+x+x²+...+x^2006-2007/x-1 ( en utilisant A^n-B^n)
ensuite
on a (X-1)/X-1 + (x²-1)/x-1 +X^3-1)/x-1 +....+(x^2006-1)/x-1
=1+2+3+4+5+6+...2006
ben tu peux ensuite utiliser de tes conaiscances concernant les suites numeriques *
quelquesoit n appartenant a N*(on Un=u1+(n-1)1)
2006=1+n-1
2006=n
Sn=(2006-1+1)/2 *2007 = 2 013 021 tbarkallah !!
esperant !! | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  Lun 31 Jan 2011, 17:28 Lun 31 Jan 2011, 17:28 | |
| - W.Elluizi a écrit:
- Soyons un peu raisonnable,la Limite de cette fonction (et comme l'a déjà signalé Mr.Lhassane) est :
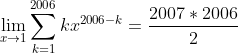 Je crois que la majorité n'on pas encore étudié la derivation - Citation :
- slt , je pense que j'ai pitetre trouver une soluce ,mais ca concorde avec ce qui a été dit auparavant :
on X^2007-2007x+2006=1+x+x²+...+x^2006-2007/x-1 ( en utilisant A^n-B^n)
ensuite
on a (X-1)/X-1 + (x²-1)/x-1 +X^3-1)/x-1 +....+(x^2006-1)/x-1
=1+2+3+4+5+6+...2006
ben tu peux ensuite utiliser de tes conaiscances concernant les suites numeriques *
quelquesoit n appartenant a N*(on Un=u1+(n-1)1)
2006=1+n-1
2006=n
Sn=(2006-1+1)/2 *2007 = 2 013 021 tbarkallah !!
esperant !! C'est ce qu'a essayer d'expliquer Bison_Futé =D | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Une limite bien compliquée .. T.T Sujet: Re: Une limite bien compliquée .. T.T  | |
| |
|
  | |
| | Une limite bien compliquée .. T.T |  |
|
