Exo intéressant

L'entier n>0 étant fixé, déterminer le nombre de couples(x,y) d'entiers strictement positifs vérifiant (1/x)+(1/y)=1/n.

un exo classique je donnerai un petit indice en spoiler

Spoiler:

Bien joué Tarask, c'est bien ça,je ne savais pas que cet exercice était si classique...
je vais poster la solution plus la peine de la garder en suspens maitenant...

Spoiler:

Voila un autre exercice :
Trouver le plus petit entier x tel que 2|x-1 , 3|x-2 ,...., 9|x-8 .

salam;

je suppose que tu veux dire que x un entier naturel.

car x s'écrit comme suit : x = -1 - k.9!
donc si k tendrait à +l'infini ==> x va tendre à - l'infini .. et par conséquant on aura jamais un plus petit entier ..


Sinon (si x > 0 ) ça sera x = -1 + (1).9! = 362879.

à + ...

Désolé {}{}=l'infini mais ta solution n'est pas correcte:
-je crois que tu veus dire "k tend vers - l'infini"
-x est bien un entier strictement positif (juste un petit oubli lors de la frappe)
-le nombre 362879 rempli les condition mais n'est pas le plus petit,loin de là...
j'éspère que tu trouveras la solution rapidement...

hhh ; oui je me suis trompé ..désolé


x = -1 + 2*3*2*5*7*2*3 = 35*72 - 1 = 2519 .


Joli exo ; merci.


Amicalement ..

{}{}=l'infini a écrit:

hhh ; oui je me suis trompé ..désolé


x = -1 + 2*3*2*5*7*2*3 = 35*72 - 1 = 2519 .


Joli exo ; merci.


Amicalement ..

Ou alors x=-1+PPCM(2,3,...,9)

D'accord ; je vais poster un autre exo pour que ça continue..

voila un exo assez intéressant :

Montrer par récurrence que

Produit (des premiers inférieurs à n ) =< 4^(n+1)

.

Exercice très très interessant et très coriace mais bien connu
il s'agit du théorème d'Erdös ^^
Bon voila la démonstration:
Montrons par récurrence sur n que le produit des nombres premiers inférieurs ou égaux à n est inférieur ou égal à 4^n
-on a pour n=3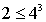
-et on a pour n=4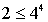
donc la relation est vraie pour tout
on suppose donc que la relation est vraie pour tout et on démontre qu'elle est vraie pour tout k=n.
On pose
*si n est pair on aura
d'où la relation est vraie
*si n est impair:
soit A le produit des nombres premiers inférieurs ou égaux (n+1)/2
et B le produit des nombres premiers strictement supérieurs à (n+1)/2 et inférieurs ou égaux à n.
selon l'hypothèse de la récurrence on a
on a par ailleurs
les facteurs premiers présents dans B sont tous présent dans et ne le sont pas dans ((n+1)/2)! et puisque ces facteurs sont premiers on a
d'où
et donc
d'autre part on sait que en remarquant que
donc
donc selon le principe de récurrence le produit des nombres premiers inférieurs ou égaux à n est inférieur ou égale à 4^n
REMARQUE : on vient de démontrer =<4^n et non 4^(n+1) demandé, ce qui est un résultat plus fin...

Allez {}{}=l'infini poste un autre exo!!faut que ça continue!!

si {}{}=l'infini le permet je vais poster un petit exo pour que le jeu continue
Trouver tous les entiers x,y et z tels que x²+y²=7z²

Bel exercice Tarask,bon choix, voila la solution:
Soit (x,y,z) un triplet de solution non nul pour l'équation en question:
Nous prossedons par étude de cas:
Cas 1:7 ne divise ni x ni y
alors x² et y² congruent nécéssairement à 1 ou 2 ou 4.
donc x²+y² ne peut être divisible par 7,or x²+y²=7z².
Cas 2: 7 divise x ou y
si 7|x alors x²=49k
donc 49k+y²=7z²
d'ou 7|y²=> 7|y (7est un nombre premier)
et de même si 7|y.
donc si 7divise x ou y ,7 divise xet y.
soit x=7k et y=7k'
on a 7z²=49k²+49k'²
donc z²=7(k+k')
d'où 7|z² => 7|z. on pose z=7k"
on a alors 49k²+49k'²=7(49k"²)
en divisant l'équation par 49 on obtient k²+k'²=7k"²
d'où (k,k',k") aussi une solution.on procède ainsi jusqu'à obtenir un triplet de solution (x,y,z) où x et y premiers avec 7.
soit y' le nombre qui vérifie yy'≡1 [7]
on sait que x²+y²≡ [7] on multiplie par y'²et on obtient (xy')²+1≡0 [7]
d'où (xy')²≡-1 [7]
or on sait par étude des cas sur le reste de la division d'un entier par 7 que il n'existe aucun entier donc le carré congrue a -1 modulo 7.
donc la seule solution a l'équation est le triplet (0,0,0).

mais, pour aller plus loin,que peut on dir de l'équation x²+y²=5z²?

x²+y²=4z²
x et y doivent être tous les deux pairs, ça donne donc : x'²+y'²=z², une inégalité connue, qui a pour solution (m²-n²,2mn,m²+n²) tels que m,n appartiennent à IN, donc les solutions sont : (2m²-2n², 4mn, m²+n²), m,n appartiennent à IN.

moi après kk petites tentatives g trouvé que x est congru à y modulo 2 kk saurait continuer?
Sinon que quelqu'un nous poste un autre exo

ok..
Exo
Soit p un nombre premier tel que p >3
Prouvez que 7^p-6^p-1 est divisible par 43

Pour ne pas laisser tomber l'exo commencé par l'infini et prolongé par moi-meme,je dirai a Tarask que (1,2,1) est bien une solution, alors pour x≡y [2]...

et bien j'ai trouvé x≡y [2] avant que tu ne réédites l'exo
je parlais de l'équation x²+y²=4z²
sinon ça va nous aider nulle part la congruence que j'ai trouvé

P.S relis ce qu'a dit oussama , lui aussi il parlait de la même equation sinon , pour x²+y²=5z² c'est le même raisonnement que t'as fait pour mon exo (que je trouve très joli )

le même raisonnement ne marche pas puisque la première n'admet pas de solution entière non nulle, alors que la seconde en admet beaucoup...
pur oussama je me suis excusé directement auprès de lui pour ma petite faute de frappe et merci pour le compliment.
Avec presque le meme raisonnement que tout a l'heure, j ai trouvé que les triplets pour k et k' deux entiers naturels.
mais je ne suis pas sûr que ce soit les seuls solutions...

pour k=k'=0 la solution n'est pas juste , reste à prouver que pour tous k,k' de N* les solutions sont justes
bon je crois que ta réponse est juste voilà pour s'assurer
est une solution
alors d'après l'équation on a
tu peux enlever le 5^k'

si si la solution marche aussi pour k=k'=0: 1²+2²=5*1²

ah wi j'ai du oublié de multiplier par 2 dans y !
peux-tu poster la solution complète ?

P.S:pour soukki , dsl si on discute pas l'exo que t'as posé , mais dès qu'on aura fini avec celui là on enchaine avec le tien

comme convenu voila en j'en suis:
Cas 1 :5 ne divise ni x ni y
on procède par étude des restes de division de x² sur 5:
x≡1 => x²≡1 [5]
x≡2 => x²≡4 [5]
x≡3 => x²≡4 [5]
x≡4 => x²≡1 [5]
nous avons alors les 8 couples de congruences qui vérifient 5|x²+y²

Cas 2 : 5 divise x ou y
si 5|x alors (5k)²+y²=5z² donc 5|y² d'où 5|y
de même si 5|y on aura 5|x
alors si 5 divise x ou y alors 5 divise x et y.
on a alors x²+y²=(5k)²+(5k')² d'où 25|x²+y²
et (1)25k²+25k'²=5z² => 5|z² =>5|z
en divisant l'equation (1) par 25 on obtient le triplet (x/5,y/5,z/5) solution de l'équation , en continuant ainsi on obtient un triplet solution (x,y,z) tel que x et y premiers avec 5 ce qui nous ramène au Cas 1, et les 8 couples de congruences.
c'est là que je bloque un peu parce qu'après quelques essais je me rends compte que les quatres seuls couples qui vérifient l'equation sont

et c'est logique en fait, puisque nous avons trouvé les couples qui vérifient 5|x²+y² ce qui n'est pas suffisant pour résoudre l'équation.
ceci nous donne par exemple les triplets (1,2,1) ou (2,1,1) ou encore (4,2,2) et (2,4,2),et on peut multiplier ces solution par n'importe quel nombre puisqu'il est par la suite simplifié:
par exemple prenons (x,y,z) solution de l'equation,on aura
(kx)²+(ky)²=5(kz)²
donc les solution de l'equation sont les triplets (k,2k,k) et(2k,k,k) .

Pour ton exercice Soukaina,il est assez simple, en voici la solution:
TOUTES LES CONGRUENCES SONT [43]
on sait que 6^3≡1 d'où 6^3k≡1
ce qui nous permet de calculer:
6^(3k+1)≡6
6^(3k+2)≡-7 en sachant bien sûr que seuls 3k+1 et 3k+2 peuvent être premiers.
et 6^(6k+1)≡6
et 6^(6k+5)≡-7
on sait aussi que 7^6≡1 d'où 7^6k≡1
ce qui nous permet de calculer:
7^(6k+1)≡7
7^(6k+2)≡6
7^(6k+3)≡-1
7^(6k+4)≡-7
7^(6k+5)≡-6
mais puisque p est premier,il ne peut être égal qu'à 6k+1 et 6k+5.
et aussi 7^3≡-1 d'où 7^(3k+1)≡7(-1)^k et 7^(3k+2)≡7²*(-1)^k≡6(-1)^k
étudions maintenat les quatres cas dégagés:
p=3k+1
7^(3k+1)-6^(3k+1)-1≡7(-1)^k-6-1
p étant premier k est obligatoirement pair
d'où 7^(3k+1)-6^(3k+1)-1≡0
p=3k+2
7^(3k+2)-6^(3k+2)-1≡6(-1)^k+7-1
p étant premier k est obligatoirement impair
d'où 7^(3k+2)-6^(3k+2)-1≡-6+7-1≡0
p=6k+1
7^(6k+1)-6^(6k+1)-1≡7-6-1≡0
p=6k+5
7^(6k+5)-6^(6k+5)-1≡-6-(-7)-1≡0
d'où si p premier et p>3 7^p-6^p-1≡0
c a d 43|7^p-6^p-1 pour p premier stricrement superieur a 3.