Exercice:

x et y sont deux réels vérifiant: x²+y²+xy=1.
Démontrez que y.x^3+x.y^3>=-2.
Bonne chance.

l'inégo est équivalente à xy(1-xy)>=2 en posant X=xy
on obtient -X²+X-2>= 0 le discriminant est négatif donc ....
je crois ke c plutôt le contraire non?
prenez x= 0 et y=1 !

tarask a écrit:

l'inégo est équivalente à xy(1-xy)>=2 en posant X=xy
on obtient -X²+X-2>= 0 le discriminant est négatif donc ....
je crois ke c plutôt le contraire non?
prenez x= 0 et y=1 !

Faute de frappe.
C'est édité.

J'ai bien aimé que quelqu'un écrive la réponse, un souhaît qui n'est pas été atteint.
La voici:
On a .
Posons et .
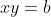
Alors .
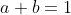
On a .
Donc .
Ce qui équivaut à .
Donc .
Donc .
Considérons le trinôme .
Ce trinôme a pour discriminent .
Donc .
Donc .
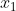
Ainsi l'équation admet deux solutions distincts, et .
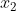
Donc et .
Donc et .
Donc et .
Donc et .
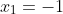
Donc et .
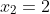
Donc le trînôme a un signe négatif entre ses racines.
Ainsi b est solution de l'inéquation si et seulement si .
Alors pour qu'on aît .
Il suffit tout simplement de démontrer que .
Au travail:
On a .
Donc .
Donc .
Donc .
Donc .
Ainsi .==>(1)
Et on a .
Donc .
Donc .
Donc .
Donc .==>(2)
De 1 et 2, on le résultat voulu.
Sauf erreur.

nmo a écrit:

J'ai bien aimé que quelqu'un écrive la réponse, un souhaît qui n'est pas été atteint.
.

Je crois avoir répondu à ton inégalité

nmo a écrit:

J'ai bien aimé que quelqu'un écrive la réponse, un souhaît qui n'est pas été atteint.

J'ai voullu postulé ma solution, mais je n'avait pas du temps.
Bon voiçi ma solution:

* y*x^3+x*y^3 >= -2 <=> xy(x^2+y^2) >= -2 <=> -(x^2+y^2)^2+(x^2+y^2)+2 >= 0. Le discrément est positive donc -(x^2+y^2+1)(x^2+y^2-2) >= 0 (A)
* On a x²+y² >= 2xy et x²+y²+xy=1 donc x^2+y^2 >= 2/3 alors -(x^2+y^2+1) =< 0
* Maintenant il suffit de démontrer que (x^2+y^2-2) =< 0 <=> x^2+y^2-2(x^2+y^2+xy) =< 0 <=> x^2+y^2+2xy >= 0 <=> (x+y)² >=0 Ce qui est juste ...

CQFD.

voilà ma solution:
on x²+y²+xy=1
=> x^3*y + y^3*x = xy- (xy)²
on doit demontrer que x^3*y + y^3*x >= -2
<=> xy - (xy)² >= -2
on a : (x+y)² = 1+xy >= 0
on a : (x-y)² = 1-3xy >= 0
=> -1 =< xy =< 1/3
=> lxyl =< 1
=> xy>= -1 et -(xy)²>= -1
=> xy-(xy)² >= -2 CQFD