Inégalité

Bonsoir tout le monde !

personne ??

Bonsoir Sherlock
facile je crois nn ?
on considère la fonction :

Sauf erreur

La dérivée est fausse. Le terme (b^a)' ne s'annule pas ...

Othmaann a écrit:

La dérivée est fausse. Le terme (b^a)' ne s'annule pas ...

Oooops oui vous avez raison

EDIT: une petite question : en considérant g(a)=b^a n'aura-t-on pas g'(a)=ln(b)*exp[a*ln(b)] ?

Indice : travailler sur la fonction , ça peut aider.

.

SOIT EMPLOYER (1+x)^a>=1+ax.

SOIT a>=b ALORS a^b+b^a>=2b^b ET CONSIDERER LA FONC f(b)=b^{b} TELS QUE 0<b<1 ( DECROISSANTE -------- CROISSANTE

Bonjour,
on peut utiliser la méthode de tarask, (à othmaann :dans ce cas on a considérer a comme variable et b comme constante, sinon c'est une fonction qui dépend de deux variable, ce qui est hors programme pour les lycéens).

achraf_djy a écrit:

Bonjour,
on peut utiliser la méthode de tarask, (à othmaann :dans ce cas on a considérer a comme variable et b comme constante, sinon c'est une fonction qui dépend de deux variable, ce qui est hors programme pour les lycéens).

Oui , considérer a comme variable et b comme constante MAIS le b est à la puissance a c'est pour ça que j'avais édité mon message :

tarask a écrit:

Othmaann a écrit:

La dérivée est fausse. Le terme (b^a)' ne s'annule pas ...

Oooops oui vous avez raison

EDIT: une petite question : en considérant g(a)=b^a n'aura-t-on pas g'(a)=ln(b)*exp[a*ln(b)] ?

Oui c'est bien ça tarask , ce qui revient a dire g'(a) = lnb.b^a

Yasser.R a écrit:

SherlocK a écrit:

Bonsoir tout le monde !

Pour
t'as utilisé
c'est bien cela ?

SherlocK a écrit:

Pour
t'as utilisé
c'est bien cela ?

Oui c'est cela, j'ai édité ma solution avec plus de détails...
J'éspère que c'est assez clair

Il faut avoir
]0;1[

non ?

Sinon d'après ce que j'ai compris t'as prouvé que :

]0;1[

puisque t'as posé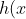

]0;1[

ne faudrait-il pas plutôt avoir :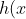








P.S: Excusez si je dis n'importe quoi ... Je ne sais rien encore sur les fonctions exponentielles

Oui oui h(x)=x^x est simple à étudier, elle admet un minimum absolu en 1/e,de plus elle est prolengeable en 0.
La relation h(x)>e^(-1) est vrai pour tout x>0.

Yasser.R a écrit:

Oui oui h(x)=x^x est simple à étudier, elle admet un minimum absolu en 1/e,de plus elle est prolengeable en 0.
La relation h(x)>e^(-1) est vrai pour tout x>0.

Merci ^^ Tout est clair maintenant

slt ^^ :
je donne une indication: il suffit de prouver

a^b>a/a+b pour tt a>0 et 0<b<1