Sporovitch
Maître
 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 | | Sujet: Il existe toujours une inégalité plus forte ... Sam 25 Sep 2010, 13:50 | |
| BoNjouur Soient a,b,c >0 Tout le mOnde sait que :  ah noon Il exitse une autre plus forte et il s'agit de :  ah noon non C'est pas encore finit Il existe toujours une autre beaucoup plus forte .. 1)Trouver un X en fonction de a,b,c telle que l'inégalité suivante sera vérifiée pour tous a,b,c >0 :  sachant que  et  avec P,Q,R des nombres réels qui ne sont pas relatifs à (a,b,c) ... 2) Mq qu'il existe une infnité de Y en fonction de a,b,c tel que 
Dernière édition par Sporovitch le Sam 25 Sep 2010, 16:06, édité 3 fois | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Il existe toujours une inégalité plus forte ... Sam 25 Sep 2010, 15:25 | |
| Tout est dû à la formule : 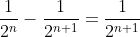 A partir de cette formule, on prouve par récurrence que : 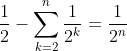 . Alors, en multipliant les deux côtés par ^2) , que voilà qu'on tombe sur : ^2}{2}%20-%20\sum_{k=2}^{n}\frac{\sum_{cyc}%20(a-b)^2}{2^k}%20=%20\frac{\sum_{cyc}%20(a-b)^2}{2^n}) . Et étant donné que le côté droit de cette dernière formule est clairement positif, il s'ensuit que : ^2}{2}%20\geq%20\sum_{k=2}^{n}\frac{\sum_{cyc}%20(a-b)^2}{2^k}) Ou encore : ^2}{2^k}) . CQFD. | |
|
Sporovitch
Maître
Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
| | Sujet: Re: Il existe toujours une inégalité plus forte ... Sam 25 Sep 2010, 15:37 | |
| Salut tout le monde Salut Dijkschneier Absolument ... Il reste mnt la premiere question qui est plus importante  | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Il existe toujours une inégalité plus forte ... Sam 25 Sep 2010, 15:41 | |
| - Sporovitch a écrit:
- Il reste mnt la premiere question qui est plus importante
Bah.. Il suffit de prendre n=3 dans la dernière formule prouvée, et de poser X = le côté droit de la formule. | |
|
Sporovitch
Maître
Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
| | Sujet: Re: Il existe toujours une inégalité plus forte ... Sam 25 Sep 2010, 16:05 | |
| - Dijkschneier a écrit:
Bah..
Il suffit de prendre n=3 dans la dernière formule prouvée, et de poser X = le côté droit de la formule. Cela ne vérifie pas les condtions ... | |
|
Contenu sponsorisé
| | Sujet: Re: Il existe toujours une inégalité plus forte ... | |
| |
|
