Exercices de logiques:

Voici les exercices:
1-Démontrez que implique que N est un carré parfait.
2-Démontrez que si x est un réel solution de l'équation 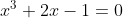alors .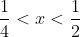
3-ABC est un triangle, R le rayon de son cercle circonscrtit, et r est le rayon de son cercle inscrit.
Démontrez que .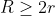
Bonne chance.

Toujours pas de réponses?
J'ajoute un autre exercice:
Est ce qu'on a ?
Que le défi se relève!
Bonne chance.

1 - Classique.
2 - Faisable en cherchant à factoriser et à tirer part des factorisations produites.
3 - Classique.
4 - Oui. En fait, il me semble que l'on a pour tout entier naturel, pgcd(a^n,b^n)=pgcd(a,b)^n.

salam

Bon voilà je vous écrirer ce que j'ai trouvé ...et si vous trouvez de fautes n'hésitez surtout pas à me les dire

1) racine(N) E Q => (a,b)E Z et N* ; a^b = 1 // racine(N) = a/b

==>(a,b)E Z et N* ; a^b = 1 // N = a²/b²
==>(a,b)E Z et N* ; a^b = 1 // N = (a/b)²

Donc on conclue que N est un carré parfait



2) x^3 +2x-1 = 0 <=> x(x²+1) + x-1 =0

<=> x-1)² +2x² + (x-1) =0

<=> x(x-1) +2x² = 0
<=> x (3x-1 ) =0

<=> x=0 ou x= 1/3

et puisque X est une solution pour l'équation

donc X = 1/3 ou X/0

on prendra X = 1/3 ; On a 1/4 < 1/3 < 1/2 <=> 1/4 < x < 1/2

et Enfin on conclue que si x est un réel solution de l'équation x^3 +2x-1 = 0 alors

1/4 < X < 1/2



4) PGCD (a;b) = 1 => E( il y a) p E Q / p= a/b

=> E( il y a) p E Q / p² = a²/b²

et on a p²E Q => a²/b² E Q

Donc p² = a²/b² => PGCD ( a²;b² ) = 1


et en enfin on conclue que PGCD (a;b) = 1 => PGCD ( a²;b² ) = 1


Voilà !!

et n'hésitez surtout pas

nami.ne a écrit:

salam
Bon voilà je vous écrirer ce que j'ai trouvé ...et si vous trouvez de fautes n'hésitez surtout pas à me les dire
1) racine(N) E Q => (a,b)E Z et N* ; a^b = 1 // racine(N) = a/b
==>(a,b)E Z et N* ; a^b = 1 // N = a²/b²
==>(a,b)E Z et N* ; a^b = 1 // N = (a/b)²
Donc on conclue que N est un carré parfait

Qui te garantis que a/b est un entier?

Citation :

2) x^3 +2x-1 = 0 <=> x(x²+1) + x-1 =0
<=> x-1)² +2x² + (x-1) =0
<=> x(x-1) +2x² = 0
<=> x (3x-1 ) =0
<=> x=0 ou x= 1/3
et puisque X est une solution pour l'équation
donc X = 1/3 ou X/0
on prendra X = 1/3 ; On a 1/4 < 1/3 < 1/2 <=> 1/4 < x < 1/2
et Enfin on conclue que si x est un réel solution de l'équation x^3 +2x-1 = 0 alors
1/4 < X < 1/2

Il s'agit bel et bien d'une solution érronée.

Citation :

4) PGCD (a;b) = 1 => E( il y a) p E Q / p= a/b
=> E( il y a) p E Q / p² = a²/b²
et on a p²E Q => a²/b² E Q
Donc p² = a²/b² => PGCD ( a²;b² ) = 1
et en enfin on conclue que PGCD (a;b) = 1 => PGCD ( a²;b² ) = 1
Voilà !!

J'invite un membre d'une large expérience à anlyser ta solution.
(Pour moi, je ne sais pas trop en arithmétiques)

nmo a écrit:

Citation :

4) PGCD (a;b) = 1 => E( il y a) p E Q / p= a/b
=> E( il y a) p E Q / p² = a²/b²
et on a p²E Q => a²/b² E Q
Donc p² = a²/b² => PGCD ( a²;b² ) = 1
et en enfin on conclue que PGCD (a;b) = 1 => PGCD ( a²;b² ) = 1
Voilà !!

J'invite un membre d'une large expérience à anlyser ta solution.
(Pour moi, je ne sais pas trop en arithmétiques)

C'est en effet un pure charabia.

Dijkschneier a écrit:

nmo a écrit:

Citation :

4) PGCD (a;b) = 1 => E( il y a) p E Q / p= a/b
=> E( il y a) p E Q / p² = a²/b²
et on a p²E Q => a²/b² E Q
Donc p² = a²/b² => PGCD ( a²;b² ) = 1
et en enfin on conclue que PGCD (a;b) = 1 => PGCD ( a²;b² ) = 1
Voilà !!

J'invite un membre d'une large expérience à anlyser ta solution.
(Pour moi, je ne sais pas trop en arithmétiques)

C'est en effet un pure charabia.

C'est ce que j'allais dire, mais j'ai peur qu'il se peut qu'il a raison.
Tu as confirmé mes soucis.

Mehdi.O a écrit:

Voici un exo :
xyz=1
Calculer S= (x+1)/(xy+x+1)+(y+1)/(y+yz+1)+(z+1)/(z+xz+1)
Un autre exo :
x+1/y=y+1/z=z+1/x
Montrez que |xyz|=1
(x;y;z)€IR^3

Pour le premier:
On a S=(x+1)/(xy+x+1)+(y+1)/(y+yz+1)+(z+1)/(z+xz+1).
Donc S=(xz+z)/(xyz+xz+z)+(z+1)/(z+xz+1)+(y+1)/(y+yz+1).
Donc S=(xz+z)/(1+xz+z)+(z+1)/(z+xz+1)+(y+1)/(y+yz+1).
Donc S=(xz+z+1)/(1+xz+z)+z/(z+xz+1)+(y+1)/(y+yz+1).
Donc S=1+ zy/(yz+xyz+y)+(y+1)/(y+yz+1).
Donc S=1+ zy/(yz+1+y)+(y+1)/(y+yz+1).
Donc S=1+ (1+zy+y)/(yz+1+y).
Donc S=1+1.
Donc S=2.
Sauf erreur.
Pour le deuxième:
On a x+1/y=y+1/z.
Donc x-y=1/z -1/y.
Donc x-y=(y-z)/zy.
Donc (x-y)zy=(y-z).==>(1)
Et par analogie (y-z)xz=(z-x).==>(2)
Et aussi (z-x)yx=(x-y).==>(3)
En multipliant 1, 2, et 3 on obient (x-y)zy(y-z)xz(z-x)yx=(x-y)(y-z)(z-x).
(On a le droit de simplifier car x, y et z sont différent deux à deux, une condition que tu as oublié).
Donc (xyz)²=1.
Donc |xyz|=1.
CQFD.
Sauf erreur.
P.S: J'ai mis "sauf erreur" deux fois car je te réponds sans brouillons.

Pour l'équation j'ai réussi a démontrer juste que x doit etre < 1/2 à vérifier :
On a x^3 +2x -1 = 0
<=> x(x^2 + 2 ) = 1
On a ab = 1 implique 3 cas :
a= 1 et b =1 :
x=1
x^2 = -1
impossible donc pas de solution dans ce cas

pour a = -1 et b= -1
x = -1
x^2 = -3
impossible

reste le 3ème cas : a = 1/b ou b = 1/a
x^2 + 2 = 1/x
=> x^2 = 1/x - 2
pour avoir une solution dans ce cas on doit avoir 1/x - 2 > 0
Soit 1/x > 2
et 0 < x < 1/2
Pour 1/4 < x je n'ai pas encore trouvé mais je continue de chercher

Si quelqu'un peut donner une solution pour PGCD ( a , b ) = 1 <=> PGCD ( a² , b² ) =1

Ca serait très intéressant car ca nous permettrait de tirer des conclusions utiles sans passer par le théorème de gauss ( qui n'est pas permis dans les examens de première . )

Mim a écrit:

Si quelqu'un peut donner une solution pour PGCD ( a , b ) = 1 <=> PGCD ( a² , b² ) =1
Ca serait très intéressant car ca nous permettrait de tirer des conclusions utiles sans passer par le théorème de gauss ( qui n'est pas permis dans les examens de première . )

Démontrable grâce au théorème fondamental de l'arithmétique.

Je n'ai pas compris ce que tu as voulu insinuer si tu peux donner un exemple ca serait appréciable et agréable de ta part

Message édité.

Dijkschneier a écrit:

Mim a écrit:

Si quelqu'un peut donner une solution pour PGCD ( a , b ) = 1 <=> PGCD ( a² , b² ) =1
Ca serait très intéressant car ca nous permettrait de tirer des conclusions utiles sans passer par le théorème de gauss ( qui n'est pas permis dans les examens de première . )

Démontrable grâce au théorème fondamental de l'arithmétique.

salam,
essai théorème de BEZOUTE .
PGCD(a^2,b^2)=1 ==>il existe (u,v)£Z^2 tq a^2u+b^2v=1 <=>a(au)+b(bv)=1 <=>au'+bv'=1 (ou u'=au£Z et v'=bv£Z)
==>pgcd(a,b)=1
refait l'autre implication (essai la forme irréductible de a/b)

Mim a écrit:

Pour l'équation j'ai réussi a démontrer juste que x doit etre < 1/2 à vérifier :
On a x^3 +2x -1 = 0
<=> x(x^2 + 2 ) = 1
On a ab = 1 implique 3 cas :
a= 1 et b =1 :
x=1
x^2 = -1
impossible donc pas de solution dans ce cas
pour a = -1 et b= -1
x = -1
x^2 = -3
impossible
reste le 3ème cas : a = 1/b ou b = 1/a
x^2 + 2 = 1/x
=> x^2 = 1/x - 2
pour avoir une solution dans ce cas on doit avoir 1/x - 2 > 0
Soit 1/x > 2
et 0 < x < 1/2
Pour 1/4 < x je n'ai pas encore trouvé mais je continue de chercher

C'est faux mon cher, on travaille dans IR et non dans IN.

On a passé une interrogation écrite pleine de trivialité la semaine précédante.
Voici les deux questions où je me suis un peu bloqué:
1-A et B sont deux ensembles faisant partie de E
Démontrez que .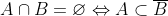
2-Démontrez que .
Bonne chance.

A n B = ensemble vide
Implique que : quelque soit x appartenant a A , x n'appartient pas a B

et on sait que x n'appartient pas a B <=> x appartient a B barre
d'ou le fait que quelque soit x appartenant a A , x appartient a B barre
Enfin , A fait partie de B barre

voila je n'ai pas utilisé les signes logiques pour que ma réponse soit claire et nette

J'attends vos avis ^^

Mim a écrit:

Je pense que ca doit etre A inter B et dans ce cas on dira puisque A inter B = ensemble vide
alors x £ A => x £/ B
donc Ax £ A , x £ B barre
donc A C B barre

sinon A U B = ensemble vide => A = ensemble vide et pareil pour B
donc B barre = l'ensemble E
et comme l'ensemble vide C E
alors A C E

mais je ne suis pas sur de la dernière déduction ( B = ensemble vide => B barre = E )

Ce qui est en bleu, dans ce cas est vrai.

1/ A n B = Ensemble vide <=> (Pour tout x £ A): x n'appartient pas à B <=> (x£A => x£B(barre)) <=> A C B(barre)
2/ Remarquer que 2/3 = 1- 1/3 donc il suffit de MQ: 1/3 n'appartient à ID ça veut dire que la dévision de 1 sur 3 nest pas précis.

Je l'ai résolu, je posterai ma solution demain.

Mim a écrit:

Je pense que ca doit etre A inter B et dans ce cas on dira puisque A inter B = ensemble vide

Oui, c'est une faute d'inattention.
C'est édité.
La solution que tu me présentes semble ambigue, essaie de rectifier.

message édité

salam

pour 2/3 n'est pas décimal:
----------------------------------

par l'absurde

si oui alors 2/3 = N/10^p

===> 2.10^p = 3.N

comme 3 n divise pas 2 ====> 3 divise 10

ce qui est impossible.

_______________________________

houssa a écrit:

salam
pour 2/3 n'est pas décimal:
----------------------------------
par l'absurde
si oui alors 2/3 = N/10^p
===> 2.10^p = 3.N
comme 3 n divise pas 2 ====> 3 divise 10
ce qui est impossible.
_______________________________

Bien, je suis d'accord.

Mim a écrit:

A n B = ensemble vide
Implique que : quelque soit x appartenant a A , x n'appartient pas a B
et on sait que x n'appartient pas a B <=> x appartient a B barre
d'ou le fait que quelque soit x appartenant a A , x appartient a B barre
Enfin , A fait partie de B barre
voila je n'ai pas utilisé les signes logiques pour que ma réponse soit claire et nette

Pourqoi a-t-on ce qui est en rouge?

Rappelons nous de la regle générale :

A inter B signifie les éléments qui se trouvent a la fois en A et en B .
Par exemple : A = {1,2,3} et B={1,b,c} alors A inter B = {1} si on avait B={a , b ,c } on aurait eu A inter B = ensemble vide .
Si A inter B = ensemble vide , ça veut dure qu'aucun élément qui fait partie de A ne fais pas partie de B

Mim a écrit:

Rappelons nous de la regle générale :
A inter B signifie les éléments qui se trouvent a la fois en A et en B .
Par exemple : A = {1,2,3} et B={1,b,c} alors A inter B = {1} si on avait B={a , b ,c } on aurait eu A inter B = ensemble vide .
Si A inter B = ensemble vide , ça veut dure qu'aucun élément qui fait partie de A ne fais pas partie de B

C'est ça ce qu'il faut démontrer également.
Au plaisir.