| | Exercices de logiques: |  |
|
+4Mim nami.ne Dijkschneier nmo 8 participants |
|
| Auteur | Message |
|---|
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mar 02 Nov 2010, 17:08 Mar 02 Nov 2010, 17:08 | |
| On n'a pas a le démontrer , c'est une regle générale
A inter B = x
<=> x est le seul élément appartenant a la fois a A et B
A inter B = rien
aucun élément n'est commun entre A et B
A vous de voir | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 03 Nov 2010, 10:45 Mer 03 Nov 2010, 10:45 | |
| - Mim a écrit:
- On n'a pas a le démontrer , c'est une regle générale
A inter B = x
<=> x est le seul élément appartenant a la fois a A et B
A inter B = rien
aucun élément n'est commun entre A et B
A vous de voir Lorsqu'on corrige le test, je te partage la solution. | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 03 Nov 2010, 11:39 Mer 03 Nov 2010, 11:39 | |
| D'accord mais je suis sur que c'est la réponse ^^ par contre j'ai une question pour l'exo 2 :
a £ ID ne siginie-t-il pas que a = b * 10^n ? ( avec b et n de IZ ) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 03 Nov 2010, 14:57 Mer 03 Nov 2010, 14:57 | |
| En vue la trivialité, j'ai d'abord évité de répondre avec ma solution. Mais je vais répondre maintenant, puisque nmo semble y trouver une difficulté. Solution au problème 1 posté par nmo : La partie (=>) est triviale. Démontrons (<=) : %20=%20B\cap%20\bar{B}%20\Rightarrow%20(A\cap%20B)%20\cup%20(B\cap%20\bar{B})%20=%20\varnothing%20\Rightarrow%20A\cap%20B%20=%20\varnothing) | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 03 Nov 2010, 15:16 Mer 03 Nov 2010, 15:16 | |
| bonjour tt le monde voila déjà trois jours que j'essai de résoudre cet exo!mais en vain. voilà l'énoncé:
x et y sont des nombres réels positifs tel que:x+y =1
et n est un nombre entier naturel, prouvez en utilisant l'implication loqique que:
(1+1\x^n)(1+1\y^n)>=(1+2^n)^n
j'espère que c'est compréhensible ;jai pas pu exprimer le supérieur ou égal et la puiss
ance
merci d'avance pour votre aide! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 03 Nov 2010, 15:16 Mer 03 Nov 2010, 15:16 | |
| - Dijkschneier a écrit:
- En vue la trivialité, j'ai d'abord évité de répondre avec ma solution.
Mais je vais répondre maintenant, puisque nmo semble y trouver une difficulté.
Solution au problème 1 posté par nmo :
La partie (=>) est triviale.
Démontrons (<=) :
%20=%20B\cap%20\bar{B}%20\Rightarrow%20(A\cap%20B)%20\cup%20(B\cap%20\bar{B})%20=%20\varnothing%20\Rightarrow%20A\cap%20B%20=%20\varnothing) Joli. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Jeu 11 Nov 2010, 18:45 Jeu 11 Nov 2010, 18:45 | |
| - Dijkschneier a écrit:
- En vue la trivialité, j'ai d'abord évité de répondre avec ma solution.
Mais je vais répondre maintenant, puisque nmo semble y trouver une difficulté.
Solution au problème 1 posté par nmo :
La partie (=>) est triviale.
Démontrons (<=) :
%20=%20B\cap%20\bar{B}%20\Rightarrow%20(A\cap%20B)%20\cup%20(B\cap%20\bar{B})%20=%20\varnothing%20\Rightarrow%20A\cap%20B%20=%20\varnothing) Merci bien, le professeur a utilisé une solution se basant sur la valeur de l'ensemble vide. Si tu veux en savoir plus, indique-le dans un message. J'ai une question et j'aime avoir une solution très prochainement: Y a-t-il un implication ou une équivalence entre les deux propositions suivantes, avec a#b: 1-  . 2-(x=1 ou x=0). Ou, il n'y a rien? Merci d'avance pour la solution. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Jeu 11 Nov 2010, 20:12 Jeu 11 Nov 2010, 20:12 | |
| Si x est un réel et a et b des entiers, il y a en effet une équivalence.
a étant différent de b, on peut supposer par symétrie des rôles que a>b <=> a - b >= 1
Et de fait, x^a = x^b <=> x^b(x^(a-b) - 1) = 0 <=> ... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  Mer 01 Déc 2010, 19:12 Mer 01 Déc 2010, 19:12 | |
| - nmo a écrit:
- 2-Démontrez que si x est un réel solution de l'équation
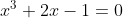 alors alors 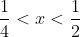 . .
Bonne chance. On démontrera donc, que pour tout réél, l'implication: : x^3+2x-1=0\Rightarrow \frac{1}{4}<x<\frac{1}{2}) . La démontrastion suivante est pour x n'importe quel réél: On a  . (L'implication contraposée) Donc  . Donc  .==>(*) (la loi de disjonction des cas) Cas premier:  . On a  . Donc  . Donc  . Donc  .==>(1) Deuxième cas:  . Et d'une manière analogue à la précédante, on aboutit à  .==>(2) De 1 et 2, on déduit que * est vraie. Donc : x^3+2x-1=0\Rightarrow \frac{1}{4}<x<\frac{1}{2}) . CQFD. Sauf erreur.
Dernière édition par nmo le Ven 28 Jan 2011, 12:28, édité 1 fois (Raison : Corriger le Latex) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Exercices de logiques: Sujet: Re: Exercices de logiques:  | |
| |
|
  | |
| | Exercices de logiques: |  |
|
