princessdesmaths
Maître
 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 | | Sujet: exercice de logique Mer 27 Oct 2010, 13:46 | |
| a , b et c appartiennent a R+* a²+b²+c² < 2 , * montrez que (1/a)+ (1/b) +(1/c) different de 1/(abc)  | |
|
Dijkschneier
Expert sup
 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: exercice de logique Mer 27 Oct 2010, 14:16 | |
| Ah oui ?
Prendre a=b=c=sqrt(1/3) | |
|
louis
Maître
Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
| | Sujet: Re: exercice de logique Mer 27 Oct 2010, 18:32 | |
| - princessdesmaths a écrit:
- a , b et c appartiennent a R+*
a²+b²+c² < 2 ,
* montrez que (1/a)+ (1/b) +(1/c) different de 1/(abc)
L'exercice est: Montrez(1/a)+(1/b)-(1/c)#(1/abc) avec (a, b, c)appartenant à IR^3 et (a^2)+(b^2)+(c^2)<2. | |
|
louis
Maître
Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
| | Sujet: Re: exercice de logique Mer 27 Oct 2010, 18:56 | |
| Voici ma solution de l'exercice: On suppose que  Donc  Donc 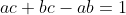 Et on a ^2=a^2+b^2+c^2-2(ac+bc)+2ab) Donc ^2+2(ac+bc)-2ab=a^2+b^2+c^2) Donc ^2+2(ac+bc-ab)=a^2+b^2+c^2) Donc ^2+2=a^2+b^2+c^2) Donc  Ce qui contredit avec  Donc  CQFD. | |
|
Mim
Maître
Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
| | Sujet: Re: exercice de logique Mer 27 Oct 2010, 19:04 | |
| - louis a écrit:
- Voici ma solution de l'exercice:
Donc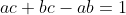
Et on a Je n'ai pas trop compris la relation / le passage ici , si tu peux éclairer ça serait agréable de ta part  EDIT : Ah c'est bon j'ai compris , je n'ai pas été assez vigilant au début ^^ | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| |
Contenu sponsorisé
| | Sujet: Re: exercice de logique | |
| |
|
