Préparations !!

Salam tout le monde,
Voilà pour améliorer notre niveau en maths
Nous allons poster des exercices au fur et à mesure dans différents domaines
Commençons par des exercices d'applications :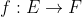

Tel que

Montrer que ( f injective )

salam :

===> clé : double inclusion

<=== clé : A= {x} et B={y} avec x différent de y

________________________________

Des solutions détaillés svp !!

salam E: appaetient , c : inclus

===>?

on part de f injective

Soit yE f(AnB) ===> y=f(x) avec x E(AnB)

===> xEA et xEB ====> f(x) E f(A) et f(x) E f(B)

===> y E f(A)nf(B)

conclusion1: f(AnB) c f(A)nf(B)
___________

soit yEf(A)nf(B) ====> y =f(a) , aEA et y =f(b) , bEB

comme f injective ====> a=b ====> y=f(x) , x=a=b E AnB

===> yE f(AnB)

conclusion2 : f(A)nf(B) c f(AnB)
__________
Enfin : f(AnB) = f(A)nf(B)

-----------------------------------------------
<===?
on part de l'égalité pour prouver l'injection

soient x et y tels que f(x) = f(y) = z

par l'absurde : supposons x =/= y

A={x} et B={y}

f(AnB) =f(vide) = vide

f(A)nf(B) = {f(x)}n{f(y)} = {z} non vide =====>contradiction

donc nécessairement x = y ====> f injective.

.

Excellent Houssa !!
Postes un exercice !

salam

je vous propose :

exo :

Soit A une partie non vide fixée d'un ensemble E

f: P(E) ------------> P(E)

X ------------> Y telle que : Y = A(delta) X = (A-X)u(X-A)

montrer que f est bijective.

____________________________

Solution du problème 2:

* Montrons d'abord que f est surjective :
Donc nous devons montrer que : ( Pour tout Z € P(E))( E X € P(E)) : f(X) = Z
f(X)=Z <=> Y=Z
<=> (A-X)(X-A)=Z
<=> (AUX)n((non A)U(nonX))=Z
<=> Zn(AnX)=Ensemble vide
Donc en prenant X = {ensemble vide} l'équation est vérifiée pour tout Z € P(E)
Donc f est surjective (1)

*Montrons que f est injective :
f(X)=f(X') => (A-X)U(X-A)=(A-X')U(X'-A)
Donc nous devons montrer que X=X'
Ici nous avons deux cas :
1- x€X-A=> x€X et x €/ A
=> x € (A-X)U(X-A)
=> x € (A-X')U(X'-A)
=> (x€A et x €/ X') ou (x€X' et x €/ A)
et puisque x €/ A donc juste x€X' et x€/ A
Il en résulte que x € X'
donc X C X' et puisque X et X' ont deux roles symétriques on montre de même que X' C X
Donc X =X'

2- x € AnX => x €/ (A-X)U(X-A)
=> x€/ (A-X')U(X'-A)
=> x €/ (A-X')
x € AnX => x € X'
X C X' et on montre de même que X' C X
Donc X=X'

Et donc f est injective .

Il s'ensuite que f est bijective

salam

7e ligne.....

Donc en prenant X = {ens.vide} etc............ pour tout ZE P(E) ????????????

FAUX : pour Z = nonA , V = vide

f(V)=(A-V)u(V-A) = AuV =A loin de Z.

_____________________

houssa a écrit:

salam

7e ligne.....

Donc en prenant X = {ens.vide} etc............ pour tout ZE P(E) ????????????

FAUX : pour Z = nonA , V = vide

f(V)=(A-V)u(V-A) = AuV =A loin de Z.

_____________________

Ce que tu as dit est dans la première équation !!
Moi j'ai pris dans la dernière équation ...
Je l'ai develloppé !!

salam

Mehdi.O

_______________
Tu as écris:

Donc en prenant X = {ens.vide} , l'équation est vérifiée pour tout Z E P(E)

____________________

ceci signifie

f(Vide) = Z pour tout Z EP(E) ??????? est-ce logique ???

.

salam

si personne ne répond , je peux donner la réponse

remarque : c'est un exercice du BELIN classe 1ère CDE (prog 1970)

_____________________

houssa a écrit:

salam
si personne ne répond , je peux donner la réponse
remarque : c'est un exercice du BELIN classe 1ère CDE (prog 1970)
_____________________

Il serait gentil si tu attends un peu, merci d'avance.

salam
Je ne sais pas si c'est la méthode souhaité mais on peut utiliser la fonction caractéristique.
On aura même que la fonction f est une involution si mes calculs sont bons.
Merci !!

salam Othmaann

pour l'involution oui ...MAIS tu dois démontrer l'associativité de "Delta" avant ;

chose déjà faite il y a longtemps dans ce forum.

salam
Pour éviter se perdre dans les calculs vaut mieux utiliser la fonction caractéristique , que ce soit pour l'associativité ou pour tout autre calcul avec la différence symétrique ... enfin , personnellement je préfère
merci.

houssa a écrit:

salam
je vous propose :
exo :
Soit A une partie non vide fixée d'un ensemble E
f: P(E) ------------> P(E)
X ------------> Y telle que : Y = A(delta) X = (A-X)u(X-A)
montrer que f est bijective.
____________________________

On a f bijective <=> .
(Voici la démonstration: https://mathsmaroc.jeun.fr/premiere-f5/preparations-aux-olympiades-de-premiere-2010-2011-t16497-90.htm)
Donc, en ce qui concerne ton problème, il reste à prouver que .
D'une part, on a .
Donc .
Donc .
Donc .
Donc, selon les lois de Morgan, .
Donc .
Donc .==>(1)
D'autre part, on a .
Donc .==>(2)
De 1 et 2, le résultat est ainsi prouvé.
f est donc bijective.
Sauf erreur.

nmo a écrit:

houssa a écrit:

salam
je vous propose :
exo :
Soit A une partie non vide fixée d'un ensemble E
f: P(E) ------------> P(E)
X ------------> Y telle que : Y = A(delta) X = (A-X)u(X-A)
montrer que f est bijective.
____________________________

On a f bijective <=> .
(Voici la démonstration: https://mathsmaroc.jeun.fr/premiere-f5/preparations-aux-olympiades-de-premiere-2010-2011-t16497-90.htm)
Donc, en ce qui concerne ton problème, il reste à prouver que .
D'une part, on a .
Donc .
Donc .
Donc .
Donc, selon les lois de Morgan, .
Donc .
Donc .==>(1)
D'autre part, on a .
Donc .==>(2)
De 1 et 2, le résultat est ainsi prouvé.
f est donc bijective.
Sauf erreur.

Bonjour nmo :
Une chose que je n'ai pas compris, on noous a demandé de montrer qu f est bijective mais est ce que cela équivaut à prouver que :
?

Merci bien

Voici une petite inégalité :
a et b et c sont des longeurs de côtés d'un triangle
Montrez que : a/(b+c-a)+b/(a+c-b)+c/(a+b-c) >= 3

Bon après-midi
Je donne ma solution en spoiler :

Spoiler:

Bonne continuation

Excellent !
Bon quelqu'un pourrait-il poster un exercice ?

A moi l'honneur alors
Je te propose cet exercice bien qu'il soit facile


Et puisque vous êtes dans les ensembles , en voici un autre


Bonne chance

tarask a écrit:

f est convexe sur R+ alors d'après l'inégalité de Jensen

Non ! Convexe sur ]-l'infini, 1-2]. Mais la condition que a,b et c soient les côtés d'un triangle assure que ceux-ci soient < 1/2.

Merci Tarask pour cet exo :
Bon le premier est classique : a= V5 +1 ou V5 -1 Juste des calculs
Le deuxième cependant j'ai une question , si on démontre que a et b et c € A est ce que
a+b+c € A ?
Parce que si oui bah j'ai démontré que V2003 et 1 et 2003 appartiennent à A
Alors?

Mehdi.O a écrit:

Merci Tarask pour cet exo :
Bon le premier est classique : a= V5 +1 ou V5 -1 Juste des calculs

Tu as commis une faute de signe, voici une solution:
https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/l-olympiade-de-settat-troisieme-phase-t15998.htm.
Bonne découverte.