| | Préparations !! |  |
|
|
|
| Auteur | Message |
|---|
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Ven 19 Nov 2010, 12:35 Ven 19 Nov 2010, 12:35 | |
| - Mehdi.O a écrit:
- Merci Tarask pour cet exo :
Bon le premier est classique : a= V5 +1 ou V5 -1 Juste des calculs
Le deuxième cependant j'ai une question , si on démontre que a et b et c € A est ce que
a+b+c € A ?
Parce que si oui bah j'ai démontré que V2003 et 1 et 2003 appartiennent à A
Alors? Non ! Il faut remarquer ,-voire parachuter- deux relations par récurrence  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Ven 19 Nov 2010, 13:09 Ven 19 Nov 2010, 13:09 | |
| - Mehdi.O a écrit:
- Bonjour nmo :
Une chose que je n'ai pas compris, on noous a demandé de montrer qu f est bijective mais est ce que cela équivaut à prouver que :
:\overline{f(X)}=f(\overline{X})) ? ?
Merci bien  Bien sûr que oui, Dijkschneier a fait une démonstration détaillé de ce fait. - tarask a écrit:
- l'inégalité , étant homogène , on peut supposer que a+b+c=1
Que veut-on dire par "homogène"? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Ven 19 Nov 2010, 13:16 Ven 19 Nov 2010, 13:16 | |
| l'inégalité est dite homogène si ( (a,b,c) réalise l'inégalité , alors (ka,kb,kc) la réalise aussi quelque soit k de R* ) P.S: je ne suis pas sûr de ce R* , prière de confirmer  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Ven 19 Nov 2010, 17:08 Ven 19 Nov 2010, 17:08 | |
| Voici une solution pour le 2: Ce problème se base sur 2 Lemmes: Lemme 1 : Nous avons x € A => x² € A=> (x+2-2)² € A => x+2 € A Donc 1€ A => 3€ A =>....=> 2003 € A Lemme 2 : (x-2)²€A => x€ A => x² € A donc si on prouve que (V2003)²€A=> (2+V2003)²€A=> ... => (2002+V2003)²€A=> (2004+V2003-2)² € A=> 2004+v2003 € A Or d'après la lemme 1 (V2003)²€ A donc 2004 +V2003 € A CQFD Pour le problème 1: C'est juste des calculs ( x1x2=c/a et x1+x2=-b/a ) Amicalement  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 24 Nov 2010, 15:36 Mer 24 Nov 2010, 15:36 | |
| - tarask a écrit:
- l'inégalité est dite homogène si ( (a,b,c) réalise l'inégalité , alors (ka,kb,kc) la réalise aussi quelque soit k de R* )
P.S: je ne suis pas sûr de ce R* , prière de confirmer  Comment tu m'explique le fait de supposer que la somme vaut 1? Pourqoi ce 1 et non pas 2, 3..? Merci de me répondre. P.S: J'attends que l'hebergeur que j'utilise se répare pour héberger une autre solution pour ce problème. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 24 Nov 2010, 16:19 Mer 24 Nov 2010, 16:19 | |
| Puisque la plupart des exercices proposés sont reltifs aux applications, je vous propose celui-ci: Soit f une application définie de E vers F et g une autre définie de F vers G. Démontrez que: 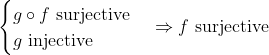 . Bonne chance.
Dernière édition par nmo le Dim 28 Nov 2010, 13:19, édité 3 fois (Raison : changer l'exercice) | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 24 Nov 2010, 16:33 Mer 24 Nov 2010, 16:33 | |
| - nmo a écrit:
- tarask a écrit:
- l'inégalité est dite homogène si ( (a,b,c) réalise l'inégalité , alors (ka,kb,kc) la réalise aussi quelque soit k de R* )
P.S: je ne suis pas sûr de ce R* , prière de confirmer  Comment tu m'explique le fait de supposer que la somme vaut 1?
Pourqoi ce 1 et non pas 2, 3..?
Merci de me répondre.
P.S: J'attends que l'hebergeur que j'utilise se répare pour héberger une autre solution pour ce problème. Bon après-midi nmo !  Un autre membre m'avait envoyé un mp me posant ainsi la même question que la tienne ! Ce genre de questions est rarement abordé (je parle d'Animath , ... ) cependant je me souviens avoir cherché à propos de ça ! Et j'ai trouvé ce lien : http://forums.futura-sciences.com/mathematiques-superieur/435078-inegalite-homogene.html Pour moi , et d'une manière un peu intuitive , j'ai compris celà en le comparant aux Polynômes Homogènes ! (jette un coup d'oeil sur Wiki  ) C'est malheureusement tout ce que je peux te donner comme explication ! Peut-être qu'on a besoin de plus d'outils pour le comprendre ! Bonne chance  | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 24 Nov 2010, 20:48 Mer 24 Nov 2010, 20:48 | |
|
salam nmo
j'ai répondu à ta question
voir mon message dans les pages précédentes posté le : sam 13 nov , 10:53
______________________________________________________________________
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 24 Nov 2010, 21:24 Mer 24 Nov 2010, 21:24 | |
| - nmo a écrit:
- tarask a écrit:
- l'inégalité est dite homogène si ( (a,b,c) réalise l'inégalité , alors (ka,kb,kc) la réalise aussi quelque soit k de R* )
P.S: je ne suis pas sûr de ce R* , prière de confirmer  Comment tu m'explique le fait de supposer que la somme vaut 1?
Pourqoi ce 1 et non pas 2, 3..?
Merci de me répondre.
P.S: J'attends que l'hebergeur que j'utilise se répare pour héberger une autre solution pour ce problème. - tarask a écrit:
- Bon après-midi nmo !

Un autre membre m'avait envoyé un mp me posant ainsi la même question que la tienne !
Ce genre de questions est rarement abordé (je parle d'Animath , ... ) cependant je me souviens avoir cherché à propos de ça ! Et j'ai trouvé ce lien : http://forums.futura-sciences.com/mathematiques-superieur/435078-inegalite-homogene.html
Pour moi , et d'une manière un peu intuitive , j'ai compris celà en le comparant aux Polynômes Homogènes ! (jette un coup d'oeil sur Wiki  ) C'est malheureusement tout ce que je peux te donner comme explication ! Peut-être qu'on a besoin de plus d'outils pour le comprendre ! ) C'est malheureusement tout ce que je peux te donner comme explication ! Peut-être qu'on a besoin de plus d'outils pour le comprendre !
Bonne chance  La raison est très simple et est tout à fait compréhensible, si elle est bien expliquée. Pour répondre à la question de nmo, on peut en fait supposer que cette somme vaut n'importe quel réel pourvu que ça ait un sens (avoir des réels positifs et supposer que leur somme est négative n'a pas de sens). Énoncé :1) Si une inégalité homogène à n variables réelles positives est vraie pour n'importe quel choix de ses variables, alors elle est aussi vraie pour n'importe quel choix de ses variables tel que leur somme soit constante (=k). 2) Inversement, si une inégalité homogène à n variables réelles positives est vraie pour n'importe quel choix de ses variables tel que leur somme soit constante (=k), alors elle est vraie pour n'importe quel choix de ses variables. Et puisque 1) et 2) sont vraies, alors pour démontrer toute inégalité homogène, il est possible d'établir une contrainte de la forme : rendre la somme des variables constante. Démonstration :1) est trivial. 2) Soit "P>=0" l'inégalité à démontrer, où P est un polynôme homogène. Soit k un réel positif. Supposons que %20\geq%200) est vraie pour tout choix de a_i tels que leur somme vaut k. On veut montrer que %20\geq%200) pour tout choix de a_i. Puisque 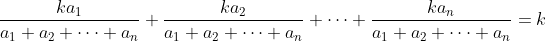 , alors %20\geq%200) d'après l'hypothèse. Et puisque P est homogène, on peut "ressortir" le terme 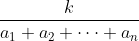 , ce qui nous donne : %20\geq%200) . Et au final : %20\geq%200) , pour tout choix des a_i. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Sam 27 Nov 2010, 18:55 Sam 27 Nov 2010, 18:55 | |
| - houssa a écrit:
salam nmo
j'ai répondu à ta question
voir mon message dans les pages précédentes posté le : sam 13 nov , 10:53
______________________________________________________________________ Je suis vraiment désolé. L'exercice est maintenant changé. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Sam 27 Nov 2010, 19:51 Sam 27 Nov 2010, 19:51 | |
| salam nmo
==========
je pense qu'il y a erreur : g injective au lieu de f
______________________________
soit y € F , g(y) = z € G
===> il existe x€ E tel que z = gof(x)
===> gof(x) = g(y)
comme g injective ====> y = f(x)
====> f surjective.
___________________________
contre exemple
a --------(f)--------> c--------(g)---------> 0
b --------(f)-------- > d--------(g)---------> 1
*****(rien)***** e -------(g)--------> 1
f inj , gof surj ; mais f non surj.
__________________________________ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Sam 27 Nov 2010, 20:22 Sam 27 Nov 2010, 20:22 | |
| - houssa a écrit:
- salam nmo
==========
je pense qu'il y a erreur : g injective au lieu de f
______________________________
soit y € F , g(y) = z € G
===> il existe x€ E tel que z = gof(x)
===> gof(x) = g(y)
comme g injective ====> y = f(x)
====> f surjective.
___________________________
contre exemple
a --------(f)--------> c--------(g)---------> 0
b --------(f)-------- > d--------(g)---------> 1
*****(rien)***** e -------(g)--------> 1
f inj , gof surj ; mais f non surj.
__________________________________ La faute provient du livre, ce n'est pas de moi. Cependant, je n'ai pas saisi ton contre exemple. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Dim 28 Nov 2010, 10:57 Dim 28 Nov 2010, 10:57 | |
|
le contre exemple est pour montrer que l'énoncé est faux
__________________ j'explique:
f : {a,b} ------> {c,d,e}
f(a)=c
f(b)=d
donc f injective
g:{c,d,e }----------> {0,1}
g(c)=0
g(d)=1
g(e)=1
donc
gof(a)=0
gof(b=1
===> gof surjective
MAIS f non surjective car e n'a pas d'antécedent par f.
___________________________________
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Dim 28 Nov 2010, 13:17 Dim 28 Nov 2010, 13:17 | |
| - houssa a écrit:
le contre exemple est pour montrer que l'énoncé est faux
__________________ j'explique:
f : {a,b} ------> {c,d,e}
f(a)=c
f(b)=d
donc f injective
g:{c,d,e }----------> {0,1}
g(c)=0
g(d)=1
g(e)=1
donc
gof(a)=0
gof(b=1
===> gof surjective
MAIS f non surjective car e n'a pas d'antécedent par f.
___________________________________ Je te comprends mainteant, mais: Seule la condition ( 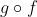 est surjective) suffit pour dire que g est surjective. Donc la deuxième condition doit être g est injective et pas f. Je vais éditer mon message immédiatement. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Mer 01 Déc 2010, 17:22 Mer 01 Déc 2010, 17:22 | |
| - nmo a écrit:
- Soit f une application définie de E vers F et g une autre définie de F vers G.
Démontrez que: 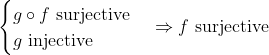 . .
Bonne chance. Je réponds alors: Supposons que 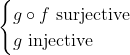 . On a, d'un côté (\exists x\in E): g\circ f(x)=z) . Donc (\exists x\in E): g(f(x))=z) . Donc (\exists y\in F): g(y)=z) , tel que f(x)=y. Donc 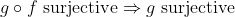 . D'un autre côté, on a 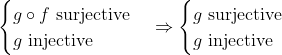 . Donc g est bijective. Donc g admet une bijection réciproque 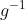 . Et puisque 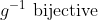 . Alors 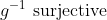 .==>(1) Etant donné que 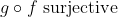 .==>(2) Il s'ensuit que 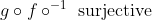 . (La composée de deux applications surjectives est bel et bien surjective) Donc 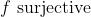 . CQFD. Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  Jeu 16 Déc 2010, 18:03 Jeu 16 Déc 2010, 18:03 | |
| - Mehdi.O a écrit:
- Voici une petite inégalité :
a et b et c sont des longeurs de côtés d'un triangle
Montrez que : a/(b+c-a)+b/(a+c-b)+c/(a+b-c) >= 3 - nmo a écrit:
- P.S: J'attends que l'hebergeur que j'utilise se répare pour héberger une autre solution pour ce problème.
Voici la solution dont je parlais:  Au plaisir. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations !! Sujet: Re: Préparations !!  | |
| |
|
  | |
| | Préparations !! |  |
|
