exercices de fonction:

Soit f la fonction définie par .
Est-ce que f admet un minimum? Justifiez vos réponses.
Bonne chance.

Je penses pas yue que -1/2 a un antecedent avec f et si oui sa va etre pas exacte mais rapproche, donc je croi qu'on doit faire une autre methode,je vais y penser!

yasserito a écrit:

Je penses pas yue que -1/2 a un antecedent avec f et si oui sa va etre pas exacte mais rapproche, donc je croi qu'on doit faire une autre methode,je vais y penser!

-1/2 n'admet plus d'antécédant.

Une autre question générale, si f admet un minimum, est-il unique? justifier.
Merci d'avance.
En d'autre mots: est-ce qu'on peut trouver une fonction à deux minimums?

Toujours, pas de réponses si intéressantes sauf celle de yumi.
Pour satisfaire ma curiosité, voici la question qui me tourmente:
Est-ce que la fonction cosinus admet un minimum? un maximum?

Oui ..la fonction cosinus admet un minimum et un maximum ( à ce que je pense )

parce que -1=< cos(x) =< 1

et cos(x) = -1 admet une solution " x = pi + 2kpi "

et cos(x) = -1 admet aussi une solution " x = 2kpi "

ou ai-je tort ??


j'attend ta réponse

à très bientôt

salam:

quand on parle du minimum ou maximum, notre intuition c'est toujours sur quel intervalle :

pour cos en [0;pi] il admet un max en 0 et un min en pi

tanmirt

Bein si f(x) = g(x)/u(x) et que g(x) admet un min ceci n'implique pas que f(x) admet un min ...
Pour cet exo je pense que la fonction admet bien un min et que le min est f(pi)=f(-pi)
déja elle est pair , la fonction cos étant périodique ( donc oscillante ) et la fonction 1/(1+V(1+x^2)) étant décroissante et vu que la limite en +00 est 0 il est clair que mon intuition est juste .
Une solution alternative serait de prouver que f(x) est décroissante sur les intervalle de la forme 0+2kpi;pi/2+2kpi et croissante sur pi/2+2kpi;pi+2kpi ensuite de montrer qu'elle est continu après on aura pour chaque petite interval le min est atteint en pi+2kpi et vu que f(pi) >f(pi+2kpi) pour tout k>0 ( un entier ) donc f(pi) est le min , j'ai bossé que sur R+ vu que la fonction est pair . Remarque avec cette preuve c'est presque trivial , mais déjà faut remarqué que la fonction admet un min ce qui n'est pas évident :p .
Amicalement

Bon, voici ma question plus simplement:
On connait que la fonction carrée admet un minimum, qui est 0, sur tout son ensemble de définition, est-ce le cas chez la fonction cosinus?
Personnellemet, je remarque la fonction cosinus admet un minimum sur chaque intervalle du type [].
Donc, soit elle admet une infinité de minimums, soit elle n'admet aucun minimum.
Je me suis pris entre deux feus, et je ne sais pas comment faire.

darkpseudo a écrit:

Bein si f(x) = g(x)/u(x) et que g(x) admet un min ceci n'implique pas que f(x) admet un min ...
Pour cet exo je pense que la fonction admet bien un min et que le min est f(pi)=f(-pi) déja elle est pair , la fonction cos étant périodique ( donc oscillante ) et la fonction 1/(1+V(1+x^2)) étant décroissante et vu que la limite en +00 est 0 il est clair que mon intuition est juste.

Je ne suis pas de ton avis, car en effet la fonction n'admet pas de minimum.
Et c'est ce qu'il faut démontrer.

nmo a écrit:

Soit f la fonction définie par .
Est-ce que f admet un minimum? Justifiez vos réponses.
Bonne chance.

Vu mon insistance sur le professeur, et comme il ne veut plus me donner la solution prête, il a proposé cet exercice dans l'évaluation.
Et voici la nouvelle version de l'exercice:
1) a-Trouvez l'ensemble de définition de la fonction f.
b-Etudier la parité de la fonction f.
2) Démontrez que f admet un maximum absolu au point 0.
3) Supposons que la fonction f admet un minimum au point .
a-Démontrez que .
b-Que peut-on déduire?
Bonne chance.

darkpseudo a écrit:

Une solution alternative serait de prouver que f(x) est décroissante sur les intervalle de la forme 0+2kpi;pi/2+2kpi et croissante sur pi/2+2kpi;pi+2kpi ensuite de montrer qu'elle est continu après on aura pour chaque petite interval le min est atteint en pi+2kpi et vu que f(pi) >f(pi+2kpi) pour tout k>0 ( un entier ) donc f(pi) est le min , j'ai bossé que sur R+ vu que la fonction est pair . Remarque avec cette preuve c'est presque trivial , mais déjà faut remarqué que la fonction admet un min ce qui n'est pas évident :p .
Amicalement

Cette solution ressemble à ce que j'ai présenté avant quelques minutes.

nmo a écrit:

Bon, voici ma question plus simplement:
On connait que la fonction carrée admet un minimum, qui est 0, sur tout son ensemble de définition, est-ce le cas chez la fonction cosinus?
Personnellemet, je remarque la fonction cosinus admet un minimum sur chaque intervalle du type [].
Donc, soit elle admet une infinité de minimums, soit elle n'admet aucun minimum.
Je me suis pris entre deux feus, et je ne sais pas comment faire.

Je crois que tu confonds deux choses : minimum et valeurs x pour lesquelles f(x) est un minimum.
La fonction cosinus a -1 comme minimum car pour tout réel x, cos(x)>=-1 et cos(PI)=-1...
Mais ce minimum est atteint à une infinité d'endroits, et c'est clair, puisque la fonction cosinus est périodique...
Le minimum, lorsqu'il existe, est unique. Mais il peut être atteint plusieurs fois.

Dijkschneier a écrit:

Le minimum, lorsqu'il existe, est unique. Mais il peut être atteint plusieurs fois.

C'est ça ce que je peux garder, et qui est utile pour moi.
Mais peut-on parler d'une fonction à deux minimums? trois ou plus?

Non.

Dijkschneier a écrit:

Non.

Merci bien.
Ainsi la fonction proposée, admet au plus um minimum.
Ce qui me met dans ce tourbillon, est un autre exercice.
Le voici:
f est une fonction définie sur IR tel que .
Démontrez que f ne peut pas admettre plus d'un seul minimum.
Que penses-tu?

il veulent dire que le minimum ne peut être atteint qu'en 1 point x_0 par exemple si le min est 1 alors f(x_0)=1 mais il n'y aura pas d'autre x tel que f(x) = 1
sinon t'est sûr que c'est strict car pour x=y t'aura f(x) < f(x) ??

darkpseudo a écrit:

sinon t'est sûr que c'est strict car pour x=y t'aura f(x) < f(x) ??

Oui, j'ai raison, et j'ai même la solution qu'ils ont proposé.

nmo a écrit:

darkpseudo a écrit:

Bein si f(x) = g(x)/u(x) et que g(x) admet un min ceci n'implique pas que f(x) admet un min ...
Pour cet exo je pense que la fonction admet bien un min et que le min est f(pi)=f(-pi) déja elle est pair , la fonction cos étant périodique ( donc oscillante ) et la fonction 1/(1+V(1+x^2)) étant décroissante et vu que la limite en +00 est 0 il est clair que mon intuition est juste.

Je ne suis pas de ton avis, car en effet la fonction n'admet pas de minimum.
Et c'est ce qu'il faut démontrer.

Pourquoi tu as mi le pair en rouge ?? f est bel est bien pair , et pour ne pas parler en l'air http://www.wolframalpha.com/input/?i=cos(x)/(1%2B(1%2Bx^2)^1/2) je suis passé par Wolfram quand j'ai lu ta réponse et j'ai trouvé qu'elle admet un min Peut être que j'ai encore une faute , sinon l'exo que j'ai proposé est de mon invention ( proposé avant ton exo ) mais je conseil fortement celui du prof vu que c'est un prof qui l'as préparé .
Amicalement

nmo a écrit:

darkpseudo a écrit:

sinon t'est sûr que c'est strict car pour x=y t'aura f(x) < f(x) ??

Oui, j'ai raison, et j'ai même la solution qu'ils ont proposé.

D'accord tu pourrais nous donner cette solution stp , ou bien juste m'expliquer comment ça ce fait que je trouve f(x)<f(x) ? Et merci

darkpseudo a écrit:

nmo a écrit:

darkpseudo a écrit:

sinon t'est sûr que c'est strict car pour x=y t'aura f(x) < f(x) ??

Oui, j'ai raison, et j'ai même la solution qu'ils ont proposé.

D'accord tu pourrais nous donner cette solution stp , ou bien juste m'expliquer comment ça ce fait que je trouve f(x)<f(x) ? Et merci

Voici de quoi je parle:
Supposons que f admet deux minimums dans IR.
Alors, .
Donc .==>(1)
Selon les données, on a .
Soit, en posant 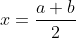, .==>(2)
On voit clairement la contradiction entre 1 et 2.
Ainsi la supposition est fausse.
Donc la fonction ne peut pas admettre plus d'un seul minimum.
P.S: S'il y a une faute, ce n'est pas de moi qui provient.

Bein je ne vois pas de faute
Fallait juste que l'énoncé précise que pour tout x et y différent car si ce sont les même la condition ne peut être rempli .
Sinon beau travail pour la preuve !

J'ai essayé le Sam 18 Déc 2010, pour ton exercise voiçi ce que j'ai pu faire:

On voit bien que f(x)=Cos(x)/(1+V(1+x²))=0 est réalisé pour x=Pi/2.
Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Pour que f(x)=Cos(x)/(1+V(1+x²)) soit minimal tel que Cos(x)<0 il faut chercher x² tel que x² est minimal pour que 1/(V(1+x²)+1) soit maximal. Donc Pi/2=<x=<Pi, et de la parité de f

Spoiler:

On déduit que -Pi=<x=<-Pi/2. Or pour tout x£[-Pi, -Pi/2] On a x>y => Cos(x)>Cos(y) (1)
Et x>y => x²<y² => V(x²+1)+1<V(y²+1)+1
<=> 1/(V(x²+1)+1) > 1/(V(y²+1)+1) ==> (2)
En multipliant (1) et (2) on aura: x>y => f(x)>f(y) , donc f est montone sur [-Pi, -Pi/2].
Donc f(x) atteint son min sur x=-pi d'ou f(x)=Cos(x)/(1+V(x²+1))>=Cos(-Pi)/(1+V(Pi²+1))
Min(f(x)) = -1/(1+V(Pi²+1)). Elle atteint son min dans deux points, Pi et -Pi

Sauf error ?