| | exercices de fonction: |  |
|
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 16:01 Dim 26 Déc 2010, 16:01 | |
| - M.Marjani a écrit:
- J'ai essayé le Sam 18 Déc 2010, pour ton exercise voiçi ce que j'ai pu faire:
On voit bien que f(x)=Cos(x)/(1+V(1+x²))=0 est réalisé pour x=Pi/2.
Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Pour que f(x)=Cos(x)/(1+V(1+x²)) soit minimal tel que Cos(x)<0 il faut chercher x² tel que x² est minimal pour que 1/(V(1+x²)+1) soit maximal. Donc Pi/2=<x=<Pi, et de la parité de f
- Spoiler:
Preuve de la parité de f:
Cos(-x)=cos(x) en plus (-x)²=x² et pour tout x£IR => -x£IR Car cos(x) est définie sur IR et 1+V(1+x²)>=1.
On déduit que -Pi=<x=<-Pi/2. Or pour tout x£[-Pi, -Pi/2] On a x>y => Cos(x)>Cos(y) (1)
Et x>y => x²<y² => V(x²+1)+1<V(y²+1)+1
<=> 1/(V(x²+1)+1) > 1/(V(y²+1)+1) ==> (2)
En multipliant (1) et (2) on aura: x>y => f(x)>f(y) , donc f est montone sur [-Pi, -Pi/2].
Donc f(x) atteint son min sur x=-pi d'ou f(x)=Cos(x)/(1+V(x²+1))>=Cos(-Pi)/(1+V(Pi²+1))
Min(f(x)) = -1/(1+V(Pi²+1)). Elle atteint son min dans deux points, Pi et -Pi 
Sauf error ? Que c'est choquant! J'ai déjà dit que f n'admet pas de minimums. Pour te convaincre, essaie avec WolframAlpha. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 16:54 Dim 26 Déc 2010, 16:54 | |
| Si elle admet un min , regarde bien avec wolfram nmo , elle admet un min globale | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 17:03 Dim 26 Déc 2010, 17:03 | |
| - darkpseudo a écrit:
- Si elle admet un min , regarde bien avec wolfram nmo , elle admet un min globale
A toi de voir: http://www.wolframalpha.com/input/?i=min+%5Cfrac%7B%5Ccos%7Bx%7D%7D%7B1%2B%5Csqrt%7B1%2Bx%5E2%7D%7D. | |
|
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 17:10 Dim 26 Déc 2010, 17:10 | |
| salam:
le fonction n'admet pas de minimum sur son domaine de définition, sinon si on parle d'un
intervalle précise, bien sur il peut avoir un min.
tanmirt | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 18:40 Dim 26 Déc 2010, 18:40 | |
| - nmo a écrit:
- darkpseudo a écrit:
- Si elle admet un min , regarde bien avec wolfram nmo , elle admet un min globale
A toi de voir:
http://www.wolframalpha.com/input/?i=min+%5Cfrac%7B%5Ccos%7Bx%7D%7D%7B1%2B%5Csqrt%7B1%2Bx%5E2%7D%7D. Au fait wolfram c'est pas le coran , elle admet un min ( les deux premier local minima dans ce que tu m'as passé ) regarde le dessin de la fonction , je pense qu'il y a un truc qui cloche dans l'algorithme de wolframalpha car dans le dessin on vois clairelement le min alors que dans la page il dit qu'il y en a pas , peut être est de à la périodicité de la fonction cos , ça a du lui brouillé le travail . | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 26 Déc 2010, 19:55 Dim 26 Déc 2010, 19:55 | |
| - nmo a écrit:
- M.Marjani a écrit:
- J'ai essayé le Sam 18 Déc 2010, pour ton exercise voiçi ce que j'ai pu faire:
On voit bien que f(x)=Cos(x)/(1+V(1+x²))=0 est réalisé pour x=Pi/2.
Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Pour que f(x)=Cos(x)/(1+V(1+x²)) soit minimal tel que Cos(x)<0 il faut chercher x² tel que x² est minimal pour que 1/(V(1+x²)+1) soit maximal. Donc Pi/2=<x=<Pi, et de la parité de f
- Spoiler:
Preuve de la parité de f:
Cos(-x)=cos(x) en plus (-x)²=x² et pour tout x£IR => -x£IR Car cos(x) est définie sur IR et 1+V(1+x²)>=1.
On déduit que -Pi=<x=<-Pi/2. Or pour tout x£[-Pi, -Pi/2] On a x>y => Cos(x)>Cos(y) (1)
Et x>y => x²<y² => V(x²+1)+1<V(y²+1)+1
<=> 1/(V(x²+1)+1) > 1/(V(y²+1)+1) ==> (2)
En multipliant (1) et (2) on aura: x>y => f(x)>f(y) , donc f est montone sur [-Pi, -Pi/2].
Donc f(x) atteint son min sur x=-pi d'ou f(x)=Cos(x)/(1+V(x²+1))>=Cos(-Pi)/(1+V(Pi²+1))
Min(f(x)) = -1/(1+V(Pi²+1)). Elle atteint son min dans deux points, Pi et -Pi 
Sauf error ? Que c'est choquant!
J'ai déjà dit que f n'admet pas de minimums.
Pour te convaincre, essaie avec WolframAlpha. C'est clair la methode, et logique en plus mon cher 
Sinon, l'avis de Amazigh-tissfola est bien plus interssante s'elle est vraiment juste  Celà montre que ma methode est juste (Car j'ai travaillé sur [-Pi, -Pi /2] et dans cet intervalle si se trouve un min pour f, serait pour pour f(x) , serait pour IR toute entiére). Donc elle atteint deux min Celà montre que ma methode est juste (Car j'ai travaillé sur [-Pi, -Pi /2] et dans cet intervalle si se trouve un min pour f, serait pour pour f(x) , serait pour IR toute entiére). Donc elle atteint deux min 
Je veux savoir comment t'as su que f(x) n'a pas de min? Si c'est avec Wolfram-Alpha: No global Min a deux sens, il n'a pas pu trouver un min de la fonction, ou ce que t'as dis. Logiquement Wolfram n'a pu selon ma methode, la methode de DarkPseudo.
Pourtant "No global Minima" veut dire aussi qu'il existe le minimum de f(x) mais dans plusieurs points:
Exemple:
f(x)= Sin(5x^3). On sait que Min(sin(5x^3))=-1. C'est quand: 5x^3=Pi/2+kpi / k£IZ => x=^3V(Pi/10+ kpi/5).
On veut voir la réaction de Wolfram Alpha: http://www.wolframalpha.com/input/?i=min+sin(5x^3)
xD... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Lun 27 Déc 2010, 16:53 Lun 27 Déc 2010, 16:53 | |
| Bon, je vais garder vos solutions jusqu'à ce que mon professeur suggère la sienne.
Merci en tout cas pour vos éclairages. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 16 Jan 2011, 15:47 Dim 16 Jan 2011, 15:47 | |
| - M.Marjani a écrit:
- Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Il n'y a aucun lien logique entre les propositions mises en rouge. S'il existe un, personnellement je ne le vois pas. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 16 Jan 2011, 16:09 Dim 16 Jan 2011, 16:09 | |
| - M.Marjani a écrit:
- J'ai essayé le Sam 18 Déc 2010, pour ton exercise voiçi ce que j'ai pu faire:
On voit bien que f(x)=Cos(x)/(1+V(1+x²))=0 est réalisé pour x=Pi/2.
Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Pour que f(x)=Cos(x)/(1+V(1+x²)) soit minimal tel que Cos(x)<0 il faut chercher x² tel que x² est minimal pour que 1/(V(1+x²)+1) soit maximal. Donc Pi/2=<x=<Pi, et de la parité de f
- Spoiler:
Preuve de la parité de f:
Cos(-x)=cos(x) en plus (-x)²=x² et pour tout x£IR => -x£IR Car cos(x) est définie sur IR et 1+V(1+x²)>=1.
On déduit que -Pi=<x=<-Pi/2. Or pour tout x£[-Pi, -Pi/2] On a x>y => Cos(x)>Cos(y) (1)
Et x>y => x²<y² => V(x²+1)+1<V(y²+1)+1
<=> 1/(V(x²+1)+1) > 1/(V(y²+1)+1) ==> (2)
En multipliant (1) et (2) on aura: x>y => f(x)>f(y) , donc f est montone sur [-Pi, -Pi/2].
Donc f(x) atteint son min sur x=-pi d'ou f(x)=Cos(x)/(1+V(x²+1))>=Cos(-Pi)/(1+V(Pi²+1))
Min(f(x)) = -1/(1+V(Pi²+1)). Elle atteint son min dans deux points, Pi et -Pi 
Sauf error ? Personnelement , je ne c'est pas si c'est faux ou vrai mais je ne vois pas pourquoi vous avez utilise la parite de f.parce que pour tout x£[Pi/2 ,Pi] on a x>y =>cos(x)<cos(y) et 1/(1+V(1+x²))<1/(1+V(1+y²)) => f(x) < f(y). alors pour tout x £ [Pi/2,Pi] ,f adment un minimum en Pi . sauf erreur et merci. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Dim 16 Jan 2011, 16:22 Dim 16 Jan 2011, 16:22 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Pour x=pi f(x)=-1/(1+V(1+pi²)) alors il existe un min de f(x) inférieur de 0 donc Cos(x)<0.
Il n'y a aucun lien logique entre les propositions mises en rouge.
S'il existe un, personnellement je ne le vois pas. Ben si j'ai bien compris ce que veut M.Marjani dire, c'est que il existe une valeur negative a f en Pi(y'a d'autres valeurs aussi).alors ce minimum doit obligatoirement ce trouver quand f est negative. et puisque 1+V(1+x²) est toujours positif alors cos(x) doit etre negatif. ce qui reduit le domaine de recherche de [-1,1] a [-1,0] alors de [-TT,TT] a [-TT,-TT/2]U[TT/2,TT]. sauf erreur et merci | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Ven 21 Jan 2011, 11:31 Ven 21 Jan 2011, 11:31 | |
| - M.Marjani a écrit:
- Monsieur! On cherche un minumum pour f : )
En effet, s'il existe un réel alpha appartenant à un intervalle -qui en le remplaçant dans cos(alpha)- fonctionne en affichant qu'il est négatif, alors f(x) sera négatif ce qu'on cherche bien, on admet que cos(alpha) sera négatif pour trouver le minimum qu'on cherche, puisqu'on travail sur IR. Pas tout à fait cela, mais c'est bien. J'ai une démonstration en tête, mais qui n'est pas parfaite. Je vais l'écrire ici pendant la prochaine vacance. Voici mon problème nouveau: Il me reste de prouver que si la fonction admet un minimum en un point, ce point n'appartient pas à l'intervalle ) . Personnellement, j'ai tant essayé mais en vain, et la solution de mon professeur n'est pas satisfaisante (elle traite un cas seulement!!). Comme ça, je peux perfectionner ma solution. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Ven 21 Jan 2011, 12:53 Ven 21 Jan 2011, 12:53 | |
| Pour rendre ma methode plus clair, je vais traduire cette phrase en un language mathématique: - Citation :
- Pour que f(x)=Cos(x)/(1+V(1+x²)) soit minimal tel que Cos(x)<0 il faut chercher x² tel que x² est minimal pour que 1/(V(1+x²)+1) soit maximal. Donc Pi/2=<x=<Pi
Soit  un réel tel que \cup%20(-\pi%20;-\frac{\pi%20}{2})) et  un réel tel que \cup%20(-\pi%20-2n\pi;-\frac{\pi%20}{2}-2n\pi%20)) et que 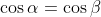 et [imghttp://latex.codecogs.com/gif.latex?n\in%20\mathbb{N}[/img  %3C%20f(\beta%20)\Rightarrow%20x\in%20(\frac{\pi%20}{2};\pi%20)\cup%20(-\pi;-\frac{\pi%20}{2}%20)) Car f(alpha) qui sera la valeur minimal. Remarquez que \cup(%20\textup{\mathrm{Domaine%20de%20}}\beta%20)=\mathbb{R}-\begin{Bmatrix}%20(2n\pi%20;\frac{\pi%20}{2}+2n\pi%20)\cup%20(-\frac{\pi%20}{2}+2n\pi%20;2n\pi%20)%20\end{Bmatrix}) Ce que j'ai voullu démontrer, c'est que si nous faisons tourner x sur le cercle trigonométrique, x prend des valeurs plus grand, puisque f(x) est négative, alors quand x prend de grand valeurs, f(x) tend vers une valeur positive, ce qui se contredit avec ce qu'on cherche. Donc l'intervalle qui suffira de l'étudier est ce que j'ai présenter. - nmo a écrit:
- M.Marjani a écrit:
- Monsieur! On cherche un minumum pour f : )
En effet, s'il existe un réel alpha appartenant à un intervalle -qui en le remplaçant dans cos(alpha)- fonctionne en affichant qu'il est négatif, alors f(x) sera négatif ce qu'on cherche bien, on admet que cos(alpha) sera négatif pour trouver le minimum qu'on cherche, puisqu'on travail sur IR. Pas tout à fait cela, mais c'est bien.
J'ai une démonstration en tête, mais qui n'est pas parfaite.
Je vais l'écrire ici pendant la prochaine vacance.
Voici mon problème nouveau:
Il me reste de prouver que si la fonction admet un minimum en un point, ce point n'appartient pas à l'intervalle ) . .
Personnellement, j'ai tant essayé mais en vain, et la solution de mon professeur n'est pas satisfaisante (elle traite un cas seulement!!).
Comme ça, je peux perfectionner ma solution. Je ne pense pas que tu vas trouver une methode, mais essaye. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  Ven 28 Jan 2011, 13:52 Ven 28 Jan 2011, 13:52 | |
| J'aime bien vous dire que l'exercice proposé par mon professeur est faux, inutile de le résoudre!!!
Je commence à avoir des soucis qui convergent vers l'existance du minimum de la fonction f.
Je demande à ceux qui maîtrisent la continuité, est-ce que vraiment la fonction admet un minimum? (sans le déterminer).
Merci d'avance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exercices de fonction: Sujet: Re: exercices de fonction:  | |
| |
|
  | |
| | exercices de fonction: |  |
|
