notre olympiade :D

voila notre olympiade
exo1 :prouver que l'equation (x-3)^10 +x^10=1 n'admet aucune solution dans IR

exo2 : x>1 et y>1 prouve que xy-x-y+1>0
exo3: a+b+c=x et 1/a + 1/b +1/c=1/x prouver que (a+b)(b+c)(a+c)=0
exo4: ABC est un triangle trouver l'emsemble des point M tel que AM=2kAB+(1-k)AC VECTEUR
EXO 5 c'est un dessin que je peut po le fair

EXO5 :
https://i.servimg.com/u/f60/16/20/55/22/sans_t11.jpg
CALCULEZ FC

salut a tous :

exo 2:
x>1 et y>1
x^3+y^3>2
-1/(x+y)>-1/2
-(x^3+y^3)/1/(x+y)>-1 (x^3+y^3)/(x+y)=x-xy+y
donc xy-x-y+1>0

exo 5:
j'ai trouvé que FC=3

pr exo 2 ya mieu (x-1)(y-1)>0 d'ou xy-x-y+1>0
ESSAIS d'expliquer un peu plus pr exo 5 (moi aussi j'ai trouvé 3)

Exo 1
Remarque: Si a et b deux réels positifs et a+b=1, alors a=<1 ET b<1 (On peut le démontrer par l'absurde...Si besoin me le signaler!)
On a : x^10>=0 et (x-3)^10>=0
Supposons que : (x-3)^10 +x^10=1
Donc x^10=<1 ET (x-3)^10=<1
Donc -1=<x=<1 ET 2=<x=<4 ABSURDE
L'équation n'admet pas de solutions réelles.

Exo 2
J'ai utilisé la même méthode que Mr. boubou math

Exo 4
Remarque : Je n'utilise que des vecteurs
AM=2k.AB+(1-k)AC
AM=2k.AB+AC-k.AC
CA+AM=k(2AB-AC)
CM=k(AB+CA+AB)
CM=k(AB+CB)
EDIT : Soit I le milieu de [AC]
AB+CB=2.IB (Toujours en vecteurs)
CM=2k.IB
Donc CM et IB sont colinéaires. Ainsi les droites (CM) et (IB) sont paralleles.
Par conséquent: L'ensemble des points M vérifiant la condition constitue la droite parallele à (IB) et passant par C

Exo 3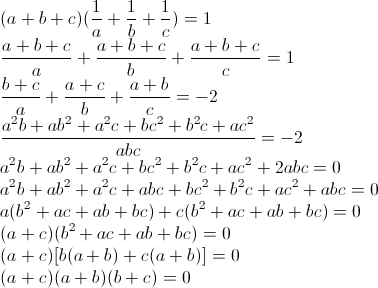

Sinon pour l'exo 5, je pense qu'il manque une donnée

bonne methode nayssi!

pr exo 4 on peut remarquer que AB+CB=-(BA+BC) soit I le milieu de AC alors BA+BC=2BI ET ON TERMINE ...
PR EXO 5 y menque aucune donnée (je l'ai fait )
sinon pr les autre exo vos methode sans exelentte

OK!
Peut-tu nous proposer la solution pour l'exo 5! J'ai pas trouvé??

exo 5: on utilise cos et sin

votre exo 5 utilises thalès et phytagore , c'est pas compliké

ou bien la technique de tassghir et takbir

Moi je pense qu'il manque une donnée : EBF est un angle droit (Ou autre qui amene à ce résultat)
Exo 5
On a : sin ABE = 12/15 = 4/5 Donc ABE = sin(-1) 4/5
Or FBC =180 - EBF - ABE
FBC = 180-90-[sin(-1) 4/5]
FBC = 90-[sin(-1) 4/5]
De plus,
sin FBC = FC/BC soit FC=(sin FBC)*BC=[sin(90-[sin(-1) 4/5])]*5=0.6*5=3

Pour l'exo 5 ( vous compliquez trop les choses ) :
AEB et BEC sont semblables donc par Thalès EB/FC=AB/BC = 3
Or EB^2 = 15^2-12^2 = 81 donc EB=9 et donc FC = 3

darkpseudo a écrit:

Pour l'exo 5 ( vous compliquez trop les choses ) :
AEB et BEC sont semblables donc par Thalès EB/FC=AB/BC = 3
Or EB^2 = 15^2-12^2 = 81 donc EB=9 et donc FC = 3

Plutot AEB et BFC
Mais Pourquoi????

mc-smailox a écrit:

Nayssi a écrit:

Exo 1
Remarque: Si a et b deux réels positifs et a+b=1, alors a=<1 ET b<1 (On peut le démontrer par l'absurde...Si besoin me le signaler!)
On a : x^10>=0 et (x-3)^10>=0
Supposons que : (x-3)^10 +x^10=1
Donc x^10=<1 ET (x-3)^10=<1
Donc -1=<x=<1 ET 2=<x=<4 ABSURDE
L'équation n'admet pas de solutions réelles.

?????

ui pk il sont semblables