Notre olympiade (FES 6 Mai )

EXO1
on a les donné suivant
0--->2
1---->4
2---->8
3---->6
0,1,2,3 le nombre de livre et 2,4,8,6 nombre de livre lu pa l’élève
trouver le minimum de et le maximum de n le nombre de livre lue par les élèves
EXO2
résoudre le système suivent
x+y+xy=11
y+z+yz=14
z+x+zx=19
EXO3
Prouver que pour tous a et b de IR
on a l'inégalité suivante
(1+a²)(1+b²)>=a(1+b²)+b(1+a²)
EXO4
Soit ABC un triangle rectangle tel que AB=10 AC=8 soit E de [AB] et G de [AC]et AG=5 et AE=4 , F est un point tel que AEFG est un triangle ,es-que F appartient a [BC]
EXO5
Soit (C) avec un centre O et (C') ac un centre O' deux cercle tangente kharijiwane dans un point A ,E de (C)et F de (C') tel que (AE)_l_(AF) prouver que (O'F)//(OE)

Tu peux poster stp la solution de lex 4 , pr savoir si F appartien ou pa ?

il y a deux méthodes
j'ecris les grandes ligne car c'est un peu long
la première est procéder par thalles et prouver que BE/AB est différant de CF/CB cela est facile a prouver en utiliser Pythagore
La deuxieme est avec les vecteur on prouve que BC=kCF+k'CG P?ON supose que f est de [BC] on trouve CG=x CFd'ou F n'apprient po a [BC]

boubou math a écrit:

EXO1
on a les donné suivant
0--->2
1---->4
2---->8
3---->6
0,1,2,3 le nombre de livre et 2,4,8,6 nombre de livre lu pa l’élève
trouver le minimum de et le maximum de n le nombre de livre lue par les élèves
EXO2
résoudre le système suivent
x+y+xy=11
y+z+yz=14
z+x+zx=19
EXO3
Prouver que pour tous a et b de IR
on a l'inégalité suivante
(1+a²)(1+b²)>=a(1+b²)+b(1+a²)
EXO4
Soit ABC un triangle rectangle tel que AB=10 AC=8 soit E de [AB] et G de [AC]et AG=5 et AE=4 , F est un point tel que AEFG est un triangle ,es-que F appartient a [BC]
EXO5
Soit (C) avec un centre O et (C') ac un centre O' deux cercle tangente kharijiwane dans un point A ,E de (C)et F de (C') tel que (AE)_l_(AF) prouver que (O'F)//(OE)

C'est plutôt un rectangle...

oui oui

boubou math, combien d'exos t'as réussi à résoudre?
Personnellement, j'ai résolu les 4 derniers exos en 1h... (Car il sont tous triviaux et faisables et qui ne demandent pas de grands réflexions)

j'ai fait 5 exos mais dans le premier y avais un tableau et je me suis trompé de colonne ... :'(

Tu peux poster ta méthode pour le dernier exo.

voila les solution des exos
EXO1
n est au maximum si et seulement si tous les livre lue sont differant autrement dis n=<2*0
4*1+8*2+6*3=38
n est au minimum si et seulement si le nombre des livres lue en commun est maximum d'ou n>=3^2^1=3 ( moi j'ai fait 8^6^4^2^1 ... :'( )
EXO2
le systeme
x+y+xy=11
y+z+yz=14
z+x+zx=19

x+1+y+xy=12
y+1+z+yz=15
z+1+x+zx=20


(x+1)(y+1)=12
(y+1)(z+1)=15
(x+1)(z+1)=20
le rest est banale on trouves s={(-5,-4,-6),(3,2,4)}
EXO3
c'est deja posté , ancien olympiade des tcm
EXO4
j'ai deja fait la reponse
EXO5
soit N un point de (D) tel que (D)est dans tengante des deux cercle dans A
on EâF=1/2<EOA et NâF=1/2<EOA
EâF+NâF=90
d'ou <EOA+<EOA=180
(OO') coupe les droites (EO) et (O'F) et <EOA+<EOA=180 d'ou (OE)//(FO')
AMICALEMENT

N doit etre du coté de E et F

boubou math a écrit:

voila les solution des exos
EXO1
n est au maximum si et seulement si tous les livre lue sont differant autrement dis n=<2*0
4*1+8*2+6*3=38
n est au minimum si et seulement si le nombre des livres lue en commun est maximum d'ou n>=3^2^1=3 ( moi j'ai fait 8^6^4^2^1 ... :'( )
EXO2
le systeme
x+y+xy=11
y+z+yz=14
z+x+zx=19

x+1+y+xy=12
y+1+z+yz=15
z+1+x+zx=20


(x+1)(y+1)=12
(y+1)(z+1)=15
(x+1)(z+1)=20
le rest est banale on trouves s={(-5,-4,-6),(3,2,4)}
EXO3
c'est deja posté , ancien olympiade des tcm
EXO4
j'ai deja fait la reponse
EXO5
soit N un point de (D) tel que (D)est dans tengante des deux cercle dans A
on EâF=1/2<EOA et NâF=1/2<EOA
EâF+NâF=90
d'ou <EOA+<EOA=180
(OO') coupe les droites (EO) et (O'F) et <EOA+<EOA=180 d'ou (OE)//(FO')
AMICALEMENT

Merci de rectifier, car c'est vraiment incompréhensible......

j'ai une question ,es-que c'est la dernière phase ?

Je vous propose ma méthode pour le dernier exercice.


Posons d'abord: .

Et, soit r et r' les rayons respectifs de (C) et (C').

On a O'AN est équilatéral en O', car O'A=O'N=r donc .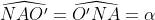
Et on a 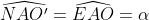car ils sont deux angles opposés par le sommet.

Et on a OAE est équilatéral car OA=OE=r donc .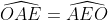


Dans le triangle O'AN on a:




Et dans le triangle OAE on a:



De (1) et (2) on conclut que AÔ'N=AÔE d'où cosAÔ'N=cosAÔE

Dans le triangle O'AN on a d'après Al-Kashi:

AN²=O'A²+O'N²-2O'A.O'N.cosAÔ'N
AN²=r'²+r'²-2.r'.r'.cosAÔ'N
AN²=2r'²-2r'².cosAÔ'N
AN²=2r'².(1-cosAÔ'N)

D'autre part, on a d'après Al-Kashi dans le triangle OAE:
AE²=OA²+OE²-2OA.OE.cosAÔE
AE²=r²+r²-2.r.r.cosAÔE
AE²=2r²-2r².cosAÔE
AE²=2r'².(1-cosAÔE)

Donc

Et on a:

De (a) et (b) on conclut que: .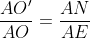

La réciperoque de Thalès donne

Et on a , alors ANF est rectangle en A, et puisque ce triangle est inscrit dans (C') ( )
D'où O le centre du cercle (C') est le milieu du diamètre [FN] donc d'où (O'N)=(O'F) (**)

De (*) et (**) on conclut que .

boubou math a écrit:

j'ai une question ,es-que c'est la dernière phase ?

Je crois que oui.

PR EXO 3
j'avais déjà vue cet exo dans c forum , j'ai essayé de me rappeler , en fin ça ma prit 1h:30 ><

ali-mes a écrit:

Je vous propose ma méthode pour le dernier exercice.


Posons d'abord: .

Et, soit r et r' les rayons respectifs de (C) et (C').

On a O'AN est équilatéral en O', car O'A=O'N=r donc .
Et on a car ils sont deux angles opposés par le sommet.

Et on a OAE est équilatéral car OA=OE=r donc .


Dans le triangle O'AN on a:




Et dans le triangle OAE on a:



De (1) et (2) on conclut que AÔ'N=AÔE d'où cosAÔ'N=cosAÔE

Dans le triangle O'AN on a d'après Al-Kashi:

AN²=O'A²+O'N²-2O'A.O'N.cosAÔ'N
AN²=r'²+r'²-2.r'.r'.cosAÔ'N
AN²=2r'²-2r'².cosAÔ'N
AN²=2r'².(1-cosAÔ'N)

D'autre part, on a d'après Al-Kashi dans le triangle OAE:
AE²=OA²+OE²-2OA.OE.cosAÔE
AE²=r²+r²-2.r.r.cosAÔE
AE²=2r²-2r².cosAÔE
AE²=2r'².(1-cosAÔE)

Donc

Et on a:

De (a) et (b) on conclut que: .

La réciperoque de Thalès donne

Et on a , alors ANF est rectangle en A, et puisque ce triangle est inscrit dans (C') ( )
D'où O le centre du cercle (C') est le milieu du diamètre [FN] donc d'où (O'N)=(O'F) (**)

De (*) et (**) on conclut que .

Je pense que j'ai une solution plus courte!!!!

postez le s'il vous plait

J'ai la mega flemme mais je vais essayer de la poster ce soir!!

Solution EXO 5

Montrer que (OE)//(O'F) revient à démontrer que : <EOA+<FO'A=180 (Deux droites parallèles coupées par une sécante forment des angles correspondants de même mesure, d'où la conclusion)

OAE et isocèle en O.
Donc <OAE=<OEA=a
Ainsi <EOA=180-2a

O'AF et isocèle en O'.
Donc <O'AF=<O'FA=b
Ainsi <FO'A=180-2b

De plus les point O', A et O sont alignés (On peut le démontrer par la perpendicularité des deux droites (O'A) et (OA) à la même droite tangente aux deux cercles en A)
Donc a+b+90=180 -> a+b=90

D'où : <EOA+<FO'A=360-2a-2b=360-2(a+b)=360-180=180 CQFD

Voilà

merçi

Pas de problèmes

c'est comme la mienne que j'ai deja posté

quelqu’un postera la solution du 3eme exercice . parce que je le résoudre difficilement avec les deltas et les polynôme . et merci d'avance .
je pesterai mon solution inchalah .

1+a²>=2a d'ou (1+a²)(1+b²)>=2a(b²+1)
1+b²>=2b d'ou (1+a²)(1+b²)>=2b(a²+1)
en faisant la somme et en simplifiant ac 2 on trouve l'inégalité demandé .