| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
+20n.naoufal sadaso maths-au-feminin Hamouda geom Azerty1995 yasserito helloall Mehdi.A Mehdi.O Meded l'intellectuelle yasmine boubou math konica Nayssi az360 expert_run upsilon ali-mes 24 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:19 | |
| Ok, je vous propose ces 2 exos:
Problème 44:
Le nombre d'habitants d'un quartier est 160 habitants, Aucun habitant ne dépasse 78 ans. Montrer qu'l existe au moins trois habitants ayant le même age.
Problème 45:
Soit ABC un triangle dont tous les angles sont aigus, et soit H l'otrthocentre de ABC.
Considérons E, F et G les projections orthogonales de A, B et C sur [BC], [AC] et [AB].
Montrer que H est le centre du cercle inscrit au triangle EFG. | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:29 | |
| Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:32 | |
| Solution du problème 44:
D'après la version généralisée du principe des tiroirs on a au moins -E(-160/78)=3 habitants ayant le même age.
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:45 | |
| je crois que Mehdi.O ne veut pas proposer un autre exo...
Donc, expert-run poste un nouveau exo. | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:47 | |
| | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:50 | |
| - Mehdi.O a écrit:
- Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG Les points A, H et E sont collinéaires ... En plus, c'est quoi D ? Je crois que tu as travaillé avec d'autres points, à toi de rectifier... | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:59 | |
| Problème 46: Montrer que l'ensemble des réels x qui vérifient l'inéquation 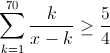 et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 20:59 | |
| - ali-mes a écrit:
- Mehdi.O a écrit:
- Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG
Les points A, H et E sont collinéaires ... En plus, c'est quoi D ?
Je crois que tu as travaillé avec d'autres points, à toi de rectifier... Oui désolé, voici les points avec lesquelles j'ai travailél, H orthocentre, D P.O de A sur BC, E sur AC et F sur AB. Amicalement. | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 21:04 | |
| - expert_run a écrit:
- Problème 46:
Montrer que l'ensemble des réels x qui vérifient l'inéquation 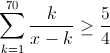et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. Cela veut-il dire que si on a une intervalle [a,b] sa longueur est b-a ?! | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 21:06 | |
| - Mehdi.O a écrit:
- expert_run a écrit:
- Problème 46:
Montrer que l'ensemble des réels x qui vérifient l'inéquation 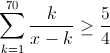et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. Cela veut-il dire que si on a une intervalle [a,b] sa longueur est b-a ?! oui c'est ça. | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 09 Juil 2011, 21:09 | |
| A savoir je ne connais pas la réponse de cet exercice ( Veuillez m'excuser puisque j'ai transgressé les régles du jeu) | |
|
| | |
kaj mima
Expert grade1
 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 13:35 | |
| - ali-mes a écrit:
- J'ai pas voulut présenter ma réponse hier, mais en tous cas je vais répondre maintenant:
Ma réponse pour problème 43:
- Spoiler:
On résous dans IN^3 l'équation: ab+ac+bc=2(a+b+c) Par symétrie de rôles, on peut supposer que: c=<b=<a. * si c=0, l'équation devient: ab=2(a+b) <=> ab-2a-2b=0 <=> a(b-2)-2b=0 <=> a(b-2)-(2b-4)=4 <=> a(b-2)-2(b-2)=4 <=> (a-2)(b-2)=4 On a: b=<a <=> b-2=<a-2 d'où (a-2=2 et b-2=2) ou (a-2=4 et b-2=1) <=> (a=4 et b=4) ou (a=6 et b=3)* si b=c=0, l'équation devient 2a=0 <=> a=0. * Maintenant supposons que: 1=<c=<b=<a:l'équation est équivalente à: ab+ac+bc-2a-2b-2c=0 <=>(ab-a-b)+(ac-a-c)+(bc-b-c)=0 <=>(a(b-1)-b)+(a(c-1)-c)+(b(c-1)-c)=0 <=>(a(b-1)-b)+(a(c-1)-c)+(b(c-1)-c)+3=3 <=>(a(b-1)-b+1)+(a(c-1)-c+1)+(b(c-1)-c+1)=3 <=>(a(b-1)-(b-1))+(a(c-1)-(c-1))+(b(c-1)-(c-1))=3 <=>(a-1)(b-1)+(a-1)(c-1)+(b-1)(c-1)=3 Avec la condition de: 1=<c=<b=<a, on obtient: 0=<(b-1)(c-1)=<(a-1)(c-1)=<(a-1)(b-1) Ainsi on a : *3=0+0+3 => (a-1)(b-1)=3 et (a-1)(c-1)=0 et (b-1)(c-1)=0 => (a-1)(b-1)=3 et a=1 et c=1 et b=1=>Absurde (on remplace a=1 et b=1 dans (a-1)(b-1)=3 et on trouve la contradiction). *3=0+1+2 => (a-1)(b-1)=2 et (a-1)(c-1)=1 et (b-1)(c-1)=0 =>(a-1)(b-1)=2 et (a-1)(c-1)=1 et b=1 et c=1 => Absurde (on remplace b=1 et c=1 dans (a-1)(b-1)=2 et (a-1)(c-1)=1 et on trouve la contradiction). *3=1+1+1 => (a-1)(b-1)=1 et (a-1)(c-1)=1 et (b-1)(c-1)=1 => a-1=1 et b-1=1 et a-1=1 et c-1=1 et b-1=1 et c-1=1 => a=2 et b=2 et c=2
Synthèse:Par conséquent: S={(4,4,0)/(0,4,4)/(4,0,4)/(6,3,0)/(3,6,0)/(0,6,3)/(0,3,6)/(3,0,6)/(6,0,3)/(2,2,2)}
A vous de me signaler si vous voyez une faute.
Tu as perdu les solutions suivantes: S'={(1,4,2),(1,2,4),(2,1,4),(2,4,1),(4,2,1),(4,1,2),(0,0,0)} P.S: la solution (0,0,0), tu l'as juste oubliée à la fin... | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 14:32 | |
| - expert_run a écrit:
- Problème 46:
Montrer que l'ensemble des réels x qui vérifient l'inéquation 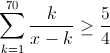et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. Solution du problème 46:Notons:  La fonction g(x) définie par g(x)=n/(x-n) avec n un entier ;est strictement décroissante quelque soit x appartenant à R/{n} Donc quelque soit x appartenant à R/{1;2;...;70} ; f(x) est strictement décroissante. Pour x<1 on a f(x)<0. On dessine le tableau de variation de f(x) sur l'intervalle [1 ;+∞ [  | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 14:36 | |
| | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 14:38 | |
| - expert_run a écrit:
- J'attends vos remarques.
Il s'agit de l'IMO 1988, P4... Ok, poste un autre exo, mais prière pour qu'il soit abordable. | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 15:05 | |
| Apparemment, expert-run n'est pas là. pour cela, je vous présente ces deux exos, pour ne pas retarder le jeu: Problème 47:Trouver toutes les fonctions définis sur IR et qui satisfont l'équation fonctionnelle: )%20=%20f(f(y))+xf(y)+f(x)-1) Problème 48: Soient m,n et p des entiers naturels non-nuls et distincts. Montrer que:  . | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 15:25 | |
| SOLUTION D'exo 48
sans nuire a la généralité de l'exercice on peut supposer que
m>n>p
or p>=1 car p est entier naturel
d'une autre part
n>1 --> n>=2
m>2--> m>=3
cela finit la démonstration . | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 16:00 | |
| - boubou math a écrit:
- SOLUTION D'exo 48
sans nuire a la généralité de l'exercice on peut supposer que
m>n>p
or p>=1 car p est entier naturel
d'une autre part
n>1 --> n>=2
m>2--> m>=3
cela finit la démonstration . Vraiment cela finit la démonstration ? A ton avis, ce que tu as fait est suffisant pour conclure que ? Faut poster des réponses complètes. | |
|
| | |
kaj mima
Expert grade1
Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 16:11 | |
| Vu la symétrie, on suppose: m>n>p avec m,n,p des entiers naturels distincts. donc on a: p>=1, puis: n>=2, et m>=3 Par suite: 1/p =< 1, 1/n =< 1/2 , 1/m =< 1/3 et m*n*p>=6 ===> 1/(m*n*p) =<1/6 En sommant, on obtient: | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 16:16 | |
| - kaj mima a écrit:
- Vu la symétrie, on suppose: m>n>p avec m,n,p des entiers naturels distincts.
donc on a: p>=1, puis: n>=2, et m>=3
Par suite:
1/p =< 1, 1/n =< 1/2 , 1/m =< 1/3 et m*n*p>=6 ===> 1/(m*n*p) =<1/6
En sommant, on obtient:
Tu peux proposer un autre problèm si tu veux. | |
|
| | |
az360
Expert grade2
Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 16:18 | |
| - ali-mes a écrit:
- kaj mima a écrit:
- Vu la symétrie, on suppose: m>n>p avec m,n,p des entiers naturels distincts.
donc on a: p>=1, puis: n>=2, et m>=3
Par suite:
1/p =< 1, 1/n =< 1/2 , 1/m =< 1/3 et m*n*p>=6 ===> 1/(m*n*p) =<1/6
En sommant, on obtient:
Tu peux proposer un autre problèm si tu veux. geometrie si tu veux ...  P /P | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 16:25 | |
| - ali-mes a écrit:
Problème 47:
Trouver toutes les fonctions définis sur IR et qui satisfont l'équation fonctionnelle:
N'oubliez pas cette équation fonctionnelle. | |
|
| | |
kaj mima
Expert grade1
Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 20:42 | |
| Solution au problème 47:Posons: ) Alors, on obtient: =f(x)+x^{2}+f(x)-1) Ce qui implique: =\frac{1-x^{2}+f(0))}{2}) Revenons à notre équation, pour x=y=0, on a: )=f(f(0))+f(0)-1) On peut remarquer que: est paire, donc: )=f(f(0))) Et par conséquent: =1) Et finalement, on obtient: =1-%5Cfrac{1}{2}x^{2}) | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 21:19 | |
| | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 10 Juil 2011, 22:05 | |
| C'est un problème de l'imo 1999. Vous pouvez trouver sa réponse ici http://www.animath.fr/IMG/pdf/cours-eqfonc.pdf
Page 34; problème 19. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> | |
| |
|
| | |
| | << Grand Jeu d'été 2011 de TC ->1ére >> | |
|
