| | TDM - Test 3 - Problème 4 |  |
|
|
| Auteur | Message |
|---|
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: TDM - Test 3 - Problème 4 Sujet: TDM - Test 3 - Problème 4  Jeu 07 Juil 2011, 20:52 Jeu 07 Juil 2011, 20:52 | |
| Problème.Soit  le milieu du cote  d'un triangle  dont tous les angles sont aigues. Soit une droite passe  coupe  et  en  et  respectivement. Soit  le centre du cercle circonscrit au triangle  et  la projection orthogonal de  sur  . Prouver que si  alors  . Auteur du Problème : Inconnu | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Jeu 07 Juil 2011, 21:39 Jeu 07 Juil 2011, 21:39 | |
| J'aimerais bien voir une réponse pour ce joli exo. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Jeu 07 Juil 2011, 23:54 Jeu 07 Juil 2011, 23:54 | |
| Une figure aprés quelques démonstrations:  Des étapes pour résoudre le probléme: - Démontrer que K,M et L sont alignés et <BAC = <KAL = 90° , les triangles ASL et AKL sont égaux.. - Démontrer que le quadrilatére AMSD est inscriptible. - Remarquer que ADP et SPM son semblables tel que p le point d'intersection de (AS) et (DM) . - Déduire que <SDM = <SMD . | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 00:11 Ven 08 Juil 2011, 00:11 | |
| - M.Marjani a écrit:
- Une figure aprés quelques démonstrations:

Des étapes pour résoudre le probléme:
- Démontrer que K,M et L sont alignés et <BAC = <KAL = 90° , les triangles ASL et AKL sont égaux..
- Démontrer que le quadrilatére AMSD est inscriptible.
- Remarquer que ADP et SPM son semblables tel que p le point d'intersection de (AS) et (DM) .
- Déduire que <SDM = <SMD . Mdr, <BAC=90  ?! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 00:18 Ven 08 Juil 2011, 00:18 | |
| - Mehdi.O a écrit:
- Mdr, <BAC=90
 ?! ?! Y a t-il quelque chose d'étrange ? Ou tu n'as pas compris le passage, et tu cherches une démonstration simple ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 00:28 Ven 08 Juil 2011, 00:28 | |
| - M.Marjani a écrit:
- Mehdi.O a écrit:
- Mdr, <BAC=90
 ?! ?!
Y a t-il quelque chose d'étrange ? Ou tu n'as pas compris le passage, et tu cherches une démonstration simple ? C'est une blague ça ?! Tu dis que <BAC=90 et tu trouves ça normal ?! C'est purement faux, quoique je suis intéressé pa ta " démonstration simple "  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 01:41 Ven 08 Juil 2011, 01:41 | |
|
Dernière édition par M.Marjani le Ven 08 Juil 2011, 11:50, édité 1 fois | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 05:26 Ven 08 Juil 2011, 05:26 | |
| Ce problème était peut-être difficile, puisque personne ne l'as résolu. Je vous propose ci-dessous ma solution. Solution.Soit K' et L' des point sur AB et AC respectivement tels que AK'L' est isocèle et M£[K'L']. Sans nuire à la généralité du problème, Supposons que K'£[AK] donc L'£[LC) et par conséquent: AK' =< AK = AL =<AL' et puisque AK'=AL' on déduit que {K',L'}={K,L} c.à.d que le couple {K,L} est unique. Soit M_a le milieu du petit arc BC du cercle circonscrit au triangle ABC. On note K_1, L_1 les projections orthogonales de M_a sur AB et AC respectivement. Il est bien connue que AM_a est la bissectrice de l'angle angle{BAC}. D'où les triangles M_aAK_1 et M_aAL_1 sont isométriques et par conséquent AK_1=AL_1, D'un autre côté, les points K_1, L_1 et M sont colinéaires sur la droite de Simson de M_a par rapport au triangle ABC. On en déduit immédiatement que {K_1,L_1}={K,L}. Soit O le centre du cercle circonscrit au triangle ABC. Puisque AM_a est l'axe radicale de (O) et (S), la droite (OS) est perpendiculaire à (AM_a). Un simple chasse angle prouve que angle{SAD}=angle{SAO}. Soit R la symétrie centrale de centre S. On note D'=R(D), O'=R(O) et M'=R(M). D'après ce qui précède, on a O'£AD, et puisque A=R(M_a), on a aussi M'£AD, et par suite O£D'M. Il est claire que MDM'D' est un parallélograme et puisque angle{MDM'}=90, il est même un rectangle de centre S, d'où on déduit que SM=SD. 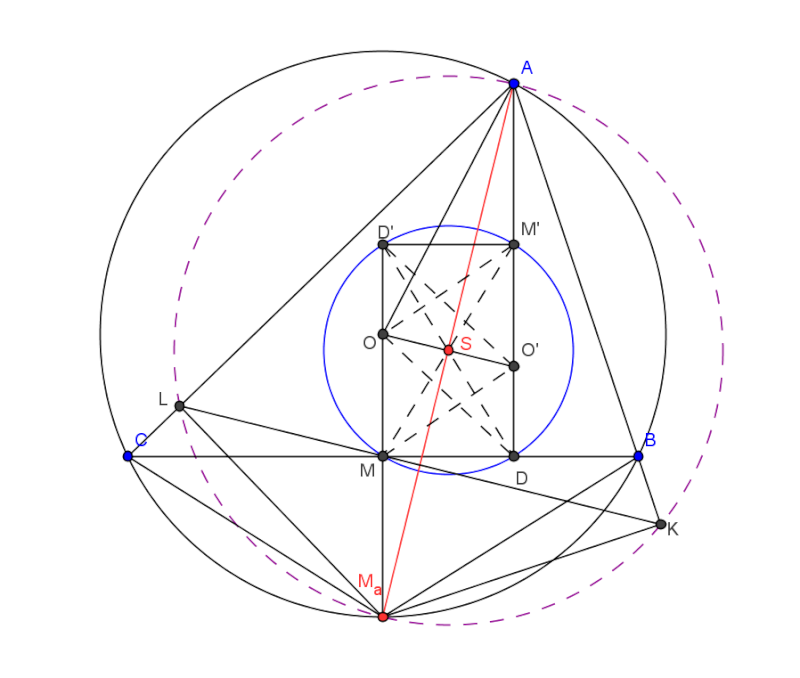 | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 11:22 Ven 08 Juil 2011, 11:22 | |
| - MohE a écrit:
- Ce problème était peut-être difficile, puisque personne ne l'as résolu. Je vous propose ci-dessous ma solution.
Solution.
Un simple chasse angle prouve que angle{SAD}=angle{SAO}. La solution parait trés belle. Je veux seulement voir ta démonstration pour ce qui en quote. Merci. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 11:44 Ven 08 Juil 2011, 11:44 | |
| - M.Marjani a écrit:
- MohE a écrit:
- Ce problème était peut-être difficile, puisque personne ne l'as résolu. Je vous propose ci-dessous ma solution.
Solution.
Un simple chasse angle prouve que angle{SAD}=angle{SAO}.
La solution parait trés belle.
Je veux seulement voir ta démonstration pour ce qui en quote. Merci. Les deux droites AD et MM_a sont parallèles, et le triangle OAM_a est isocèle, ainis angle{SAD}=angle{SM_aO}=angle{SAO} | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 12:14 Ven 08 Juil 2011, 12:14 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- MohE a écrit:
- Ce problème était peut-être difficile, puisque personne ne l'as résolu. Je vous propose ci-dessous ma solution.
Solution.
Un simple chasse angle prouve que angle{SAD}=angle{SAO}.
La solution parait trés belle.
Je veux seulement voir ta démonstration pour ce qui en quote. Merci. Les deux droites AD et MM_a sont parallèles, et le triangle OAM_a est isocèle, ainis angle{SAD}=angle{SM_aO}=angle{SAO} Comme ça la solution serait parfaite et detaillé. Trés jolie. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 17:29 Ven 08 Juil 2011, 17:29 | |
| - MohE a écrit:
 A-t-on vraiment la colinéarité des points A, M_a et S? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  Ven 08 Juil 2011, 19:10 Ven 08 Juil 2011, 19:10 | |
| Oui on l'a, et c'est bien clair non ?!
Il est bien connu que AM_a est bissectrice de l'angle {BAC}.D'une part: puisque S est le centre de AKL donc, angle{CAS}=angle{LAS}=angle{ALS}=angle{ALK}-angle{SLK}=angle{AKL}-angle{SKL}=angle{AKS}=angle{SAK}=angle{SAB} ce qui implique que AS est bissectrice de l'angle {BAC}, d'où la conclusion. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: TDM - Test 3 - Problème 4 Sujet: Re: TDM - Test 3 - Problème 4  | |
| |
|
  | |
| | TDM - Test 3 - Problème 4 |  |
|
