- Siba a écrit:
- Soit f la fonction définie de R vers R par:
|f(x)|=<1 , et: f(x+13/42) + f(x) = f(x+1/6) + f(x+1/7)
Montrer que f est périodique.
Je te proposerai une solution classique de ce problème:
Il suffit de remarquer que
.
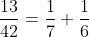
Ainsi, si on définit une fonction g par
:g(x)=f(x)-f(x+\frac{1}{7}))
l'hypothèse impliquerait que
:g(x)=g(x+\frac{1}{6}))
.
Cela veut dire que g est périodique, et sa période est
.
Maintenant, pour un x donné, les fonctions
)
ne peuvent prendre que 6 valeurs distinctes a, b, c, d, e et f, et l'on a pour tout entier n la propriété:
-f(x)=n(a+b+c+d+e+f))
.
(Cela vient, en posant pour ce x donné: g(x)=a,
=b)
et ainsi de suite, et puis on exprime la fonction g par son expression, et finalement on somme les égalité qu'on a trouvé.)
L'autre hypothèse, implique que a+b+c+d+e+f est nul. Et cela veut dire que
=f(x))
.
(Au fait, on aura
\le2)
qui n'est pas vérifié que si a+b+c+d+e+f est nul.)
Ainsi, 1 est le plus petit réel non nul réalisant
:f(x+1)=f(x))
. fest donc 1-périodique, ce qui répond à la question.
Sauf erreurs.
Accueil 
moi j'avais trouvé que sa période est de 2k/7, mais j'avais certainement fait une erreur lors de mes calculs.