| | Cinquième olympiade de première (27 Avril 2012) |  |
|
+11boubou math Oty nmo ali-mes ryuzaki L ryuzaki az360 amigo-6 Eurêka!! ryuuzaki omra alidos konica 15 participants |
|
| Combien d'exercices avez-vous résolu? | | 0 exercice | | 0% | [ 0 ] | | 1 exercice | | 0% | [ 0 ] | | 2 exercices | | 21% | [ 3 ] | | 3 exercices | | 43% | [ 6 ] | | 4 exercices | | 36% | [ 5 ] |
| | Total des votes : 14 | | | |
|
| Auteur | Message |
|---|
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Cinquième olympiade de première (27 Avril 2012) Sujet: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 18:50 Ven 27 Avr 2012, 18:50 | |
| Problème 1 : Soit f une fonction polynôme de second degré. Soient a,b, et c trois nombres réels distincts deux à deux tels que : f(a)=bc, f(b)=ac et f(c)=ab. Trouver f(a+b+c) Problème 2 : Résoudre le système:  où x,y, et z sont des nombres réels. Problème 3 : Trouver tous les nombres réels a tel qu'il existe une fonction f:R==>R vérifiant l'égalité f(sin x)+af(cos x) = cos(2x) pour tout nombre réel x. Problème 4 : Soit ABC un triangle. X et Y sont les milieux respectifs des côtés [AB] et [AC]. Soit D un point qui appartient au côté [BC] et différent du milieu de [BC]. Montrer que si <XDY = <BAC alors (AD) et (BC) sont perpendiculaires. | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 19:20 Ven 27 Avr 2012, 19:20 | |
| j'ai trouvé a l'exo 2 : ( 0.0.0 ) et (1/2 ;1/2 ;1/2 ) | |
|
  | |
ryuuzaki omra
Maître

 Nombre de messages : 164 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 19:43 Ven 27 Avr 2012, 19:43 | |
| Je n'étais pas admis pour passer cette olympiade, cela fait mal au coeur, mais je vais continuer à bosser comme même. | |
|
  | |
Eurêka!!
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 20/04/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 19:52 Ven 27 Avr 2012, 19:52 | |
| alors, y a t il quelqu'un qui propose des solutions?? | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 19:55 Ven 27 Avr 2012, 19:55 | |
|
Dernière édition par alidos le Mar 09 Oct 2012, 00:48, édité 1 fois | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 19:56 Ven 27 Avr 2012, 19:56 | |
| *pour le 1 on pose f(x)= px²+mx+c et on calcue f(a)-f(b) ainsi f(b)-f(c) et en remplant on obtient c=ab+ac+bc et p=1 et m -a-b-c ----> on conclue que f(a+b+c)=ab+ac+bc !
| |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 20:15 Ven 27 Avr 2012, 20:15 | |
| une autre solution pour 1 : on consédirons : q(x) = xf(x) - abc et ces racines sont a,b,c on devrait trouvé quelque chose  . | |
|
  | |
ryuzaki L ryuzaki
Débutant
 Nombre de messages : 1 Nombre de messages : 1
Age : 29
Date d'inscription : 27/04/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 20:32 Ven 27 Avr 2012, 20:32 | |
| moi aussi j'ai trouvé la même solution de Alidos x=y=z=1/2 ou x=y=z=0
| |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 20:45 Ven 27 Avr 2012, 20:45 | |
|
Dernière édition par alidos le Mar 09 Oct 2012, 00:48, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 20:58 Ven 27 Avr 2012, 20:58 | |
| Solution au problème 1:Soit: =\alpha%20x^2%20+%20\beta%20x+\gamma) avec alpha non nul. On a: =\alpha%20(a+b+c)^2%20+%20\beta%20(a+b+c)+\gamma%20=\sum_{a,b,c}(\alpha%20a^2%20+\beta%20a%20+%20\gamma%20)+2\alpha%20\left%20(%20ab+ac+bc%20\right%20)-2\gamma%20=(f(a)+f(b)+f(c))+2\alpha%20(f(a)+f(b)+f(c))-2f(0)=(2\alpha%20+1)(f(a)+f(b)+f(c))-2f(0)) . Si on considère le polynôme de 3eme degré g(x), tel que g(x)=xf(x)-abc, on trouve g(a)=g(b)=g(c)=0. Donc: g(x)=(x-a)(x-b)(x-c)=x^3-(a+b+c)x^2+(ab+ac+bc)x-abc ou: xf(x)-abc=x^3-(a+b+c)x^2+(ab+ac+bc)x-abc Donc: ^3%20+%20\beta%20(x)^2+\gamma%20x%20=%20x^3-(a+b+c)x^2+(ab+ac+bc)x-abc%20\Rightarrow%20\alpha=1%20\;%20\;%20\mathrm{et}\;%20\;%20\gamma%20=ab+ac+bc) . D'où: =(2%20\times%201%20+%201)(ab+ac+bc)-2(ab+ac+bc)=ab+ac+bc) Solution au problème 3: Solution au problème 3:EDIT: (Solution fausse) Solution au problème 4: Soit Z le mileu de [BC] (D est différent de Z),supposons sans nuire à la généralité du problème que D£[BZ]. Par Thalès (XZ)//(AC) et (YZ)//(AB), donc: 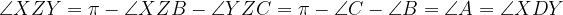 . Ainsi, le quadrilatère XYZD est inscriptible, donc D appartient à (C) le cercle circonscrit au triangle XYZ, or, il est bien connu que (C) est le cercle des neuf points du triangle ABC, et (C) coupe BC danc Z et D' l'hauteur issue de A. Et puisque: 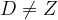 , il s'en suit que D'=D, d'où le résultat: %20\perp%20(BC%20)) . (Durant le test, j'ai démontré que D'£(C)  )
Dernière édition par ali-mes le Ven 27 Avr 2012, 22:05, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:10 Ven 27 Avr 2012, 21:10 | |
| - az360 a écrit:
- une autre solution pour 1 :
on consédirons : q(x) = xf(x) - abc et ces racines sont a,b,c on devrait trouvé quelque chose  . . Très bien, similaire à ma solution. Par symétrie de la situation, on distingue deux cas: L'un des réels a, b et c est nul; ou l'autre cas où les trois ne sont pas nuls. Pour le second cas, on procède ainsi: On remarque ainsi que q est de la forme q(x)=k(x-a)(x-b)(x-c), pour tout réel x, tel que k est une constante. De plus, on a q(0)=0.f(0)-abc=-abc et q(0)=k(0-a)(0-b)(0-c)=-kabc. Ce qui veut bien dire -abc=-kabc, et donc k=1. Et ainsi (x-a)(x-b)(x-c)=x.f(x)-abc, pour tout réel x, précisément pour x=a+b+c on obtient (a+b+c).f(a+b+c)-abc=(a+b)(b+c)(c+a). Ce qui devient (a+b+c).f(a+b+c)=abc+(a+b)(b+c)(c+a). Ou encore (a+b+c).f(a+b+c)=(a+b+c)(ab+bc+ca). Et finalement f(a+b+c)=ab+bc+ca, bien sûr si a+b+c est différent de 0. Et si a+b+c=0, on doit remarquer que =a(-a-b)=-ab-a^2) , =b(-a-b)=-ab-b^2) et =ab) . D'où la fonction cherchée est sans doute =-a^2-b^2+x^2-ab) , pour tout réel x. Et donc =-a^2-b^2-ab=-a(-b-c)-b(-a-c)-ab=ab+bc+ca) . Pour l'autre cas, on suppose par symétrie que c=0, il s'ensuit que f(a)=0 et f(b)=0 avec f(0)=ab. On sait que f(x) est de la forme f(x)=h(x-a)(x-b), pour tout réel h, tel que h est une constante. Or, f(0)=hab et f(0)=ab donc hab=ab et par conséquent h=1. On écrit donc f(x)=(x-a)(x-b) pour tout réel x, et donc f(a+b+c)=f(a+b)=ab+bc+ca. Synthèse: Dans tous les cas, on aura f(a+b+c)=ab+bc+ca. Sauf erreurs.
Dernière édition par nmo le Ven 27 Avr 2012, 21:19, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:14 Ven 27 Avr 2012, 21:14 | |
| J'adresse à ceux qui ont fait le 2eme de partager avec nous la solution, car c'est l'exercice que j'ai raté durant le test. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:25 Ven 27 Avr 2012, 21:25 | |
| pour le 2) voila ce que j'ai fait : on remarque que si l'un des nombres x ou y ou z sont nul alors x=y=z=0 . Mnt pour x,y,z différent de 0 , posant a=2x .... en multipliant l'es 3 égalité il vient que : (1+a²)(1+b²)(1+c²)=8abc , or par AM-GM , LHS >= 8|abc| >= 8abc avec égalité si a=b=c  on rempalce dans l'une des equation : on trouve x(2x-1)²=0 ..... | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:26 Ven 27 Avr 2012, 21:26 | |
|
Dernière édition par boubou math le Ven 27 Avr 2012, 21:52, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:26 Ven 27 Avr 2012, 21:26 | |
| Je rerédigerai un autre jour si j'ai pas trop la flemme .
Dernière édition par darkpseudo le Ven 27 Avr 2012, 22:00, édité 2 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:27 Ven 27 Avr 2012, 21:27 | |
| @nmo , es ce que tu peux posté votre épreuve si c possible Merci . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:33 Ven 27 Avr 2012, 21:33 | |
| - boubou math a écrit:
- ali-mes a écrit:
- J'adresse à ceux qui ont fait le 2eme de partager avec nous la solution, car c'est l'exercice que j'ai raté durant le test.
Pour le 2 , il suffit de remarquer que si l'un de x,y et z est negatif alors le systèmes n'admet pas de solution ainsi , x>=0,y>=0,z>=0
avec IAG 1+4x²>=4x implique xy>=z² de même yz>=x² et xz>=y², en sommant il nous viens 1/2[(x-y)²+(y-z)²+(x-z)²]=<0 impliqe x=y=z et le reste est trivial . C'est faux ! cela implique z^2>=xy. La solution de darkpseudo était juste ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:45 Ven 27 Avr 2012, 21:45 | |
| - Oty a écrit:
- @nmo , es ce que tu peux posté votre épreuve si c possible Merci .
Je n'ai pas reçu le test, mais un certain des membres du forum l'a scanné pour moi. Je ne sais pas si c'est interdit de le partager sur Internet ou non. (Ce sont les conseils des encadrants lors des stages) | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 21:51 Ven 27 Avr 2012, 21:51 | |
| - ali-mes a écrit:
- Solution au problème 1:
Soit: =\alpha%20x^2%20+%20\beta%20x+\gamma) avec alpha non nul. avec alpha non nul.
On a: =\alpha%20(a+b+c)^2%20+%20\beta%20(a+b+c)+\gamma%20=\sum_{a,b,c}(\alpha%20a^2%20+\beta%20a%20+%20\gamma%20)+2\alpha%20\left%20(%20ab+ac+bc%20\right%20)-2\gamma%20=(f(a)+f(b)+f(c))+2\alpha%20(f(a)+f(b)+f(c))-2f(0)=(2\alpha%20+1)(f(a)+f(b)+f(c))-2f(0)) . .
Si on considère le polynôme de 3eme degré g(x), tel que g(x)=xf(x)-abc, on trouve g(a)=g(b)=g(c)=0.
Donc: g(x)=(x-a)(x-b)(x-c)=x^3-(a+b+c)x^2+(ab+ac+bc)x-abc
ou: xf(x)-abc=x^3-(a+b+c)x^2+(ab+ac+bc)x-abc
Donc: ^3%20+%20\beta%20(x)^2+\gamma%20x%20=%20x^3-(a+b+c)x^2+(ab+ac+bc)x-abc%20\Rightarrow%20\alpha=1%20\;%20\;%20\mathrm{et}\;%20\;%20\gamma%20=ab+ac+bc) . .
D'où: =(2%20\times%201%20+%201)(ab+ac+bc)-2(ab+ac+bc)=ab+ac+bc)
Solution au problème 3:
On a: :%20f(\sin%20x)+af(%20\cos%20x)=%20\cos%20(2x))
Pour x=0, on obtient: +af(%20\cos%200)=%20\cos%200%20\Rightarrow%20f(0)+af(1)=1\;%20\;%20{:\color{Blue}%20(1)})
Pour x=pi/2, on obtient: +af(%20\cos%20\frac{\pi}{2})=%20\cos%20\pi%20\Rightarrow%20f(1)+af(0)=-1\;%20\;%20{:\color{Blue}%20(2)}) . .
+(2)}\Rightarrow%20(a+1)(f(0)+f(1))=0)
Alors: =-f(1)) . .
- Si: a=-1, on trouve que: :%20f(\sin%20x)-f(\cos%20x)=\cos(2x)) , cette relation est vérifiée pour la fonction x|->-x², car pour tout réel x, on a: , cette relation est vérifiée pour la fonction x|->-x², car pour tout réel x, on a: =%20-%20\sin^2%20x%20+\cos^2%20x=f(\sin%20x)-f(\cos%20x)) . .
Ainsi, a=-1 répond au problème.
Si: f(0)=-f(1):On remplace dans la condition initiale respectivement par x=-pi/2, et x=pi, et on trouve:
)+af(\cos%20\left%20(%20-\frac{\pi}{2}%20\right%20))=\cos%20(%20-%20\pi)\Rightarrow%20f(-1)+af(0)=-1\;%20\;%20:{\color{Blue}%20(1%27)})
)+af(\cos%20\left%20(%20\pi%20\right%20))=\cos%20(%202%20\pi)\Rightarrow%20f(0)+af(-1)=1\;%20\;%20:{\color{Blue}%20(2%27)})
+(2%27)}\Rightarrow%20(a+1)(f(0)+f(-1))=0\Rightarrow%20f(0)=-f(-1)) , donc: f(1)=f(-1). , donc: f(1)=f(-1).
-(1)}\Rightarrow%20a(f(-1)-f(1))=0\Rightarrow%20a=0) . .
Si a=0, on trouve que la relation devient: :%20f(\sin%20x%20)=\cos(2x)) . .
Et cela est vrai en considérant la fonction x|->1-2x², car pour tout réel x, on a:
=1-2\sin^2%20x%20=f(\sin%20x)) . Donc a=0 répond aussi à l'exercice. . Donc a=0 répond aussi à l'exercice.
D'où a£{0,1}.
Solution au problème 4:

Soit Z le mileu de [BC] (D est différent de Z),supposons sans nuire à la généralité du problème que D£[BZ]. Par Thalès (XZ)//(AC) et (YZ)//(AB), donc:
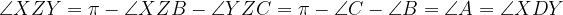 . .
Ainsi, le quadrilatère XYZD est inscriptible, donc D appartient à (C) le cercle circonscrit au triangle XYZ, or, il est bien connu que (C) est le cercle des neuf points du triangle ABC, et (C) coupe BC danc Z et D' l'hauteur issue de A.
Et puisque: 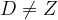 , il s'en suit que D'=D, d'où le résultat: , il s'en suit que D'=D, d'où le résultat: %20\perp%20(BC%20)) . .
(Durant le test, j'ai démontré que D'£(C)  ) )
pr le 3 j'ai procédé autrement , le résultats étais différant aussi on remplace x par 90-x il nous vient ainsi ))+af(sin(x))=-cos(2x)=-f(sin(x))-af(cos(x))\Rightarrow&space;(f(cos(x))+f(sin(x)))(a+1)=0) ainsi a=1 ou f(sin(x))=-f(cos(x)) si a=-1 la fonction f(x)=-x² resoud le problème , maintenant si f(sin(x))=-f(cos(x)) ))+af(cos(x))=cos(2x)\Rightarrow&space;f(cos(x))(a-1)=cos(2x)) si a=1 il nous vient cos(2x)=0 pour tous x , absurd donc a différant de 1 et ainsi )=\frac{2cos(x)^2-1}{a-1}) réciproquement cette fonction marche bien donc pr tous a#1 il existe une fonction qui répond a l'exo la faute dans la demo d'Ali : l'impliquation 2'-1 ---> a=0 est fausse car on a déjà f(1)=f(-1).
Dernière édition par boubou math le Ven 27 Avr 2012, 22:44, édité 4 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 22:03 Ven 27 Avr 2012, 22:03 | |
| Boubou Math ma démo de l'exo 3 est trés similaire a la tienne  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 22:06 Ven 27 Avr 2012, 22:06 | |
| - Oty a écrit:
- Boubou Math ma démo de l'exo 3 est trés similaire a la tienne
 . . Je pense qu'il y a une faute depuis le début, c'est a=-1 et non a=1. Ou bien, je ne vois pas comment on aura a=-1. J'attends que quelqu'un met cette obscurité au point. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 22:09 Ven 27 Avr 2012, 22:09 | |
| - nmo a écrit:
- Oty a écrit:
- Boubou Math ma démo de l'exo 3 est trés similaire a la tienne
 . . Je pense qu'il y a une faute depuis le début, c'est a=-1 et non a=1.
Ou bien, je ne vois pas comment on aura a=-1.
J'attends que quelqu'un met cette obscurité au point. faute d’intention c'est rectifié ... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 22:14 Ven 27 Avr 2012, 22:14 | |
| - boubou math a écrit:
- nmo a écrit:
- Oty a écrit:
- Boubou Math ma démo de l'exo 3 est trés similaire a la tienne
 . . Je pense qu'il y a une faute depuis le début, c'est a=-1 et non a=1.
Ou bien, je ne vois pas comment on aura a=-1.
J'attends que quelqu'un met cette obscurité au point. faute d’intention c'est rectifié ... je parlais de la maniére avec laquelle il a procédé , pour ma par j'ai utilisé A(pi\2-x) et A(-x) , en combinant c'est deux assértion en arrive a une égalité qui nous permet d'obtenir les valeurs de a et de discuter tout les différent cas . | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Ven 27 Avr 2012, 22:23 Ven 27 Avr 2012, 22:23 | |
| Solution sans 9 point : O le centre de [XY] D' est l'image de D par rapport au O , Z et l'image de A par rapport au O (Z aussi le milieu de [BC]) on a : AD'YX est cyclique alors :AD'X = AYX = <C d'autre part on a : <AD'X = <ZDY alors : YDC= YDZ = <C = YCD => AY = YC = DY alors ADC est rectangle  . | |
|
  | |
mathvic
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 28
Date d'inscription : 06/12/2011
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  Sam 28 Avr 2012, 09:39 Sam 28 Avr 2012, 09:39 | |
| pour 3 exercice
x=pi/4
f(sin pi/4)+af(cos pi/4)=cos2.pi/4
a=-1 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Cinquième olympiade de première (27 Avril 2012) Sujet: Re: Cinquième olympiade de première (27 Avril 2012)  | |
| |
|
  | |
| | Cinquième olympiade de première (27 Avril 2012) |  |
|
