| | Trois exercices type olympiades. |  |
|
|
| Auteur | Message |
|---|
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Trois exercices type olympiades. Sujet: Trois exercices type olympiades.  Dim 29 Avr 2012, 15:27 Dim 29 Avr 2012, 15:27 | |
| Exercice 1
Résoud dans R l'équation suivante :
V(cosx) + V(sinx) =1
Exercice 2
Comparez:
555/666
4444/5555
et 333333/444444
Exercice 3
Considérons le nombre qui s'écrit sous la forme suivante : 200020002000 .... 2000
Sachant que 2000 se répète 2000 fois .
Est ce que ce nombre est un carré (moraba3oun kamil) ?
Dernière édition par Soukaina Amaadour le Mar 08 Mai 2012, 12:45, édité 1 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Lun 30 Avr 2012, 15:52 Lun 30 Avr 2012, 15:52 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Lun 30 Avr 2012, 18:54 Lun 30 Avr 2012, 18:54 | |
| - Soukaina Amaadour a écrit:
- Exercice 3
Considérons le nombre qui s'écrit sous la forme suivante : 200020002000 .... 2000
Sachant que 2000 se répète 2000 fois .
Est ce que ce nombre est un carré (moraba3oun kamil) ? C'est le seul exercice qui apparait, je propose alors ma solution: Il est facile de remarquer que si on pose 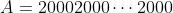 où 2000 se répète 2000 fois, alors ) , le dernier nombre se compose de 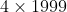 zéros. Et donc ) . Il est facile de voir que 5 divise notre A. Et pour que a soit le carré d'un entier, il faut que l'exposant de 5 dans sa décomposition en facteurs premiers soit un entier pair. Et comme 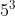 divise 2000, il faudrait au moins que 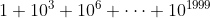 soit divisible par 5; i.e: il faut que le nombre des unités de 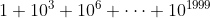 est 0 ou 5. Cela n'est pas absolument le cas car le nombre des unités de 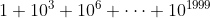 est 1. Ainsi A ne peut pas être le carré d'un entier naturel. Sauf erreurs. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Lun 30 Avr 2012, 23:08 Lun 30 Avr 2012, 23:08 | |
| pour le probleme 3 voila ce que je te propose : il est facile de montrer par une récurrence que : })=2000.\frac{10^{4n}-1}{10^4-1}) , pour n=2000 ..... | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mar 01 Mai 2012, 01:40 Mar 01 Mai 2012, 01:40 | |
| Chapeau bas à nmo et Oty  Il reste deux exos' maintenant. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mar 01 Mai 2012, 01:53 Mar 01 Mai 2012, 01:53 | |
| je crois qu'on les vois pas ces deux exos ^^ | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mar 01 Mai 2012, 20:44 Mar 01 Mai 2012, 20:44 | |
| Exo 1 : Resoud dans R l'equation: V(cosx) + V(sinx) =1
Exo 2: Comparez:
555/666
4444/5555
et 333333/444444 | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mar 01 Mai 2012, 21:02 Mar 01 Mai 2012, 21:02 | |
| exo 1: posant : t=rac(cos(x)) ; p=rac(sin(x)) , on a : t+p=1=t^4+p^4 , t(1-t^3)+p(1-p^3)=0 ,puisque 0=<t,p=<1 on a donc t (1-t^3)=0 et p (1-p^3)=0 ..... | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 02 Mai 2012, 13:04 Mer 02 Mai 2012, 13:04 | |
| - Oty a écrit:
- exo 1: posant : t=rac(cos(x)) ; p=rac(sin(x)) , on a : t+p=1=t^4+p^4 , t(1-t^3)+p(1-p^3)=0 ,puisque 0=<t,p=<1 on a donc t (1-t^3)=0 et p (1-p^3)=0 .....
Y a un cas ou p=1/2 et T=1/2 --> cosx=1/4 et sins=1/4 -..... Ta méthode ne le prend pas en compte! ?? | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 02 Mai 2012, 13:08 Mer 02 Mai 2012, 13:08 | |
| Pour le dernier ex 555/666= 5/6 et 4444/5555=4/5 et 333333/444444=3/4
5/6>4/5 et 4/5>3/4 ainsi 555/666>4444/5555>333333>444444 | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 02 Mai 2012, 13:44 Mer 02 Mai 2012, 13:44 | |
| - amigo-6 a écrit:
- Oty a écrit:
- exo 1: posant : t=rac(cos(x)) ; p=rac(sin(x)) , on a : t+p=1=t^4+p^4 , t(1-t^3)+p(1-p^3)=0 ,puisque 0=<t,p=<1 on a donc t (1-t^3)=0 et p (1-p^3)=0 .....
Y a un cas ou p=1/2 et T=1/2 --> cosx=1/4 et sins=1/4 -.....
Ta méthode ne le prend pas en compte! ?? tu es sur que ce que tu as ecris est correcte ? ton résultat donne 2 valeurs différente a ''x'' , ce qui est impossible ! | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 02 Mai 2012, 13:58 Mer 02 Mai 2012, 13:58 | |
| ah oui dsl  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 02 Mai 2012, 14:15 Mer 02 Mai 2012, 14:15 | |
|
1)trouvez les entiers x y z tel que x^3+2y^3=4z^3
2) les bissectrices intérieures des angles <B et <C d un triangle ABC coupent les cotés en B' ET C' respectivement.
Démontrer que la droite B'C' coupe le cercle inscrit dans le triangle ABC! godd luck:D
| |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mar 08 Mai 2012, 20:53 Mar 08 Mai 2012, 20:53 | |
| 1)
x^3=-2(y^3-2z^3)
x est donc pair
Concisérons x' un entier tel que x=2x'
On a donc : 8x'^3=2(2z^3-y^3)
donc: 4x' ^3=2z^3-y^3
Donc y^3= 2(z^3-2x'^3 )
y est donc pair !
Prenons: Y un entier tel que : y=2Y
Donc: 8x'^3+16Y^3=4z^3
Donc: z^3=2x'^3+2Y^3
Donc z^3=2(x'^3+Y^3)
z est aussi pair ..
Et puisque x , y et z sont des nombres pairs .. Cette équation n'a pas de solution dans IN !
Dernière édition par Soukaina Amaadour le Mer 27 Juin 2012, 23:00, édité 1 fois | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 09 Mai 2012, 14:01 Mer 09 Mai 2012, 14:01 | |
| - Soukaina Amaadour a écrit:
- 1)
x^3=-2(y^3-2z^3)
x est donc pair
Concisérons x' un entier tel que x=2x'
On a donc : 8x'^3=2(2z^3-y^3)
donc: 4x' ^3=2z^3-y^3
Donc y^3= 2(z^3-2x'^3 )
y est donc pair !
Prenons: Y un entier tel que : y=2Y
Donc: 8x'^3+16Y^3=4z^3
Donc: z^3=2x'^3+2Y^3
Donc z^3=2(x'^3+Y^3)
z est aussi pair ..
Et puisque x , y et z sont des nombres pairs .. Cette équation n'a pas de solution dans R !
T es sur ? prend le cas x=y=z=0 | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 09 Mai 2012, 21:29 Mer 09 Mai 2012, 21:29 | |
| Attend , un entier = 3adad 2awali c'est ça ?
Et d'après mes connaissances, un entier ne peu être divisé que par 1 et lui même !
Mais 0 se divise par tous les nombres non ?
| |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 09 Mai 2012, 21:40 Mer 09 Mai 2012, 21:40 | |
| - Soukaina Amaadour a écrit:
- Attend , un entier = 3adad 2awali c'est ça ?
Et d'après mes connaissances, un entier ne peu être divisé que par 1 et lui même !
Mais 0 se divise par tous les nombres non ?
Non , 3adad awali = nombre premier | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 09 Mai 2012, 22:17 Mer 09 Mai 2012, 22:17 | |
| | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  Mer 09 Mai 2012, 23:11 Mer 09 Mai 2012, 23:11 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Trois exercices type olympiades. Sujet: Re: Trois exercices type olympiades.  | |
| |
|
  | |
| | Trois exercices type olympiades. |  |
|
