| | Inégalité |  |
|
|
| Auteur | Message |
|---|
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Inégalité Sujet: Inégalité  Dim 03 Juin 2012, 20:38 Dim 03 Juin 2012, 20:38 | |
| Prouvez que \in&space;\mathbb{R+}^{3},&space;\Rightarrow&space;\frac{ab}{a+b}+\frac{ac}{a+c}+\frac{bc}{b+c}\leq&space;\frac{a+b+c}{2}) | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 20:44 Dim 03 Juin 2012, 20:44 | |
| on a : a+b >= 2 rac (ab) et b+c >= 2 rac (bc) et a+c >= 2 rac (ac) 1/a+b =< 1/ 2 rac (ab) et 1/b+c =< 1/ 2 rac (bc) et 1/a+c =< 1/ 2 rac (ac) ab/a+b =< rac (ab)/2 et bc/b+c =< rac (bc) /2 et ac/a+c =< rac (ac )/2 On Prenons en compte cette inegalité a+b+c >= rac ab +rac bc +rac ac on déduit Le résultat  | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 | |
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 21:13 Dim 03 Juin 2012, 21:13 | |
| En voilà une autre: Prouvez que: \in&space;\mathbb{R+}^{3}&space;avec&space;\rightarrow&space;a+b+c=1) 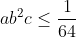 | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 21:25 Dim 03 Juin 2012, 21:25 | |
| a b² c je crois n'est ce pas | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 21:33 Dim 03 Juin 2012, 21:33 | |
| - alidos a écrit:
- a b² c je crois n'est ce pas
Oui c'est ce que j'ai ecrite. non ? | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 22:49 Dim 03 Juin 2012, 22:49 | |
|  Voila Ma Solution | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 03 Juin 2012, 22:50 Dim 03 Juin 2012, 22:50 | |
| | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 | |
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Lun 04 Juin 2012, 15:57 Lun 04 Juin 2012, 15:57 | |
| Mais je peux te demander un truc ?
Comment t'as ecrit ta démo' ? | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Mar 25 Sep 2012, 22:26 Mar 25 Sep 2012, 22:26 | |
| voila la bonne réponse:
on a : (a-b)^2>=0 puis a^2+b^2+2ab>=4ab alors (a+b)^2>=4ab donne a+b/4>=ab/a+b
de la même manière on prouve que a+c/4>=ca/c+a et que b+c/4>= bc/b+c
on aura : ab/a+b + bc/b+c + ca/c+a>=(2a+2b+2c)/4
enfin : ab/a+b + bc/b+c + ca/c+a>=(a+b+c)/2 | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Mar 25 Sep 2012, 22:36 Mar 25 Sep 2012, 22:36 | |
| les réponses de Alidos et Soukaina sont FAUTES | |
|
  | |
Top-Math
Féru
 Nombre de messages : 59 Nombre de messages : 59
Age : 27
Date d'inscription : 11/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Sam 29 Sep 2012, 15:13 Sam 29 Sep 2012, 15:13 | |
| - L-W-P a écrit:
- voila la bonne réponse:
on a : (a-b)^2>=0 puis a^2+b^2+2ab>=4ab alors (a+b)^2>=4ab donne a+b/4>=ab/a+b
de la même manière on prouve que a+c/4>=ca/c+a et que b+c/4>= bc/b+c
on aura : ab/a+b + bc/b+c + ca/c+a>=(2a+2b+2c)/4
enfin : ab/a+b + bc/b+c + ca/c+a>=(a+b+c)/2 Dèja voilà une petite faute mais bon c'est rien - L-W-P a écrit:
- les réponses de Alidos et Soukaina sont FAUTES
Comment peux-tu affirmer cela. Leurs réponse sont justes ^^ . Si tu trouves que c'est faux, PROUVE LE ![b] | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Dim 07 Oct 2012, 22:02 Dim 07 Oct 2012, 22:02 | |
| Bonsoir tout le monde  , a+b+c=1 tels que a, b et c > 0 , démontrer que (1+1/a)(1+1/b)(1+1/c) >= 64 | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  Lun 08 Oct 2012, 23:50 Lun 08 Oct 2012, 23:50 | |
| Bonsoir on a avec Hölder  avec AM -GM on a  D'ou la Conclusion | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Inégalité Sujet: Re: Inégalité  | |
| |
|
  | |
| | Inégalité |  |
|
