| | Problèmes depuis la Roumanie: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Problèmes depuis la Roumanie: Sujet: Problèmes depuis la Roumanie:  Dim 05 Aoû 2012, 14:36 Dim 05 Aoû 2012, 14:36 | |
| Problème1:Suppose 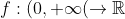 is a non constant function with the property that -f(y)|\le|\sin{x}-\sin{y}|) , forall 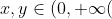 . Prove that f is periodic bounded function and 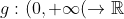 ; =f(x)+x) is a monotomic function. Problème2:Let 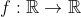 be a function such that )=2^x-1) , for all real numbers x. Show that +f(1)=1) Problème3: Problème3:Let _{n\ge1}) be a sequence of non-negative integers such 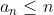 for all 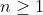 , and }=0) , for all 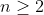 . Find a closed formula for the general term of the sequence. Problème4:Let a and b two rational numbers such that the absolute value of the complex number 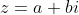 be equal to 1. Prove that the absolute value of the complex number 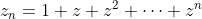 is a rational number for all odd integers n. Bonne chance. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Lun 06 Aoû 2012, 10:58 Lun 06 Aoû 2012, 10:58 | |
| Pb1
On pose µ=pi, qqs x>=0,
|f(x)-f(x+2µ)| =<|sin(x)-sin(x+2µ)|=0 ==> f(x+2µ)=f(x) Donc f est 2µ périodique
qqs x,y>=0, |f(x)-f(y)| =<|sin(x)-sin(y)| =<|x-y| ==> f est continue sur R+
f continue est périodique ==> f bornée
qqs x>y>=0, |f(x)-f(y)| =<|sin(x)-sin(y)| =<x-y ==> f(y)-f(x) =<x-y ==> g croissante sur R+
| |
|
  | |
YIRA
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 30
Date d'inscription : 13/01/2011
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 18:23 Mar 07 Aoû 2012, 18:23 | |
| Peux-je avoir la solution du 2eme exercice nmo ? | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 19:17 Mar 07 Aoû 2012, 19:17 | |
| - YIRA a écrit:
- Peux-je avoir la solution du 2eme exercice nmo ?
il me semble : que d'apres l'equation initial on a : f(2^x-1)=2^f(x) - 1 => pour x=0 , f(0)=2^f(0) - 1 et pour x=1 f(1)=2^f(1)-1 , ainsi il suffit de montrer que l'equation 2^{x}=x+1 admet seulement deux solution {0 , 1} sur R ce qui permetra de conclure que f(0)+f(1)=1 . (sauf erreur ) | |
|
  | |
YIRA
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 30
Date d'inscription : 13/01/2011
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 20:52 Mar 07 Aoû 2012, 20:52 | |
| - Oty a écrit:
- YIRA a écrit:
- Peux-je avoir la solution du 2eme exercice nmo ?
il me semble : que d'apres l'equation initial on a : f(2^x-1)=2^f(x) - 1 => pour x=0 , f(0)=2^f(0) - 1 et pour x=1 f(1)=2^f(1)-1 , ainsi il suffit de montrer que l'equation 2^{x}=x+1 admet seulement deux solution {0 , 1} sur R ce qui permetra de conclure que f(0)+f(1)=1 . (sauf erreur ) belle solution, ma méthode est analytique très longue qui repose sur le faite que fof(x)+fof(y)+fof(x)fof(y)=fof(x+y) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 21:00 Mar 07 Aoû 2012, 21:00 | |
| Merci beaucoup , au plaisir  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 23:01 Mar 07 Aoû 2012, 23:01 | |
| - Oty a écrit:
- YIRA a écrit:
- Peux-je avoir la solution du 2eme exercice nmo ?
il me semble : que d'apres l'equation initial on a : f(2^x-1)=2^f(x) - 1 => pour x=0 , f(0)=2^f(0) - 1 et pour x=1 f(1)=2^f(1)-1 , ainsi il suffit de montrer que l'equation 2^{x}=x+1 admet seulement deux solution {0 , 1} sur R ce qui permetra de conclure que f(0)+f(1)=1 . (sauf erreur ) Il faut préciser avant de conclure; ou en parallèle avec ce qui est en rouge; que f est injective. A part ça, la solution est bonne. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mar 07 Aoû 2012, 23:20 Mar 07 Aoû 2012, 23:20 | |
| - nmo a écrit:
Il faut préciser avant de conclure; ou en parallèle avec ce qui est en rouge; que f est injective.
A part ça, la solution est bonne. oui il est claire qu'elle est injectivite  , f(a)=f(b) => 2^{a}=2^{b} => a=b , Merci . | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mer 08 Aoû 2012, 12:02 Mer 08 Aoû 2012, 12:02 | |
| Pb 3
on pose µ=pi
cos(a1µ/2)=0
a1 dans {0,1} ==> a1= 1
cos(µ/3)+cos(a2µ/3)=0 ==> cos(a2µ/3)=-1/2
a2 dans {0,1,2} ==> a2=2
cos(µ/4)+cos(2µ/4)+cos(a3µ/4)=0 ==> cos(a3µ/4)=-V2/2
a3 dans {0,1,2,3} ==> a3=3
supposons que ak=k pour tout k dans {1,...,n} , n>1
cos(µ/(n+2))+cos(2µ/(n+2))+cos(3µ/(n+2))+ ...+ cos(nµ/(n+2))+cos(a(n+1)µ/(n+2))=0
==>
cos(a(n+1)µ/(n+2))
=-Re[ sum{ k=1, k=n}exp( ikµ/(n+2)) ]
=-Re[ (exp( iµ/(n+2))-exp( i(n+1)µ/(n+2)) / (1-exp( iµ/(n+2))) ]
=-Re[ (exp( iµ/(n+2))-exp( i(n+1)µ/(n+2)) / (1-exp( iµ/(n+2))) ]
=-Re[ ( exp( iµ/2(n+2)) -exp( i(n+1)µ/(n+2)- iµ/2(n+2)) /( exp( -iµ/2(n+2)) - exp( iµ/2(n+2)) ) ]
=-Re[ ( exp( iµ/2(n+2)) -exp( i(2n+1)µ/2(n+2)) /( -2isin(µ/2(n+2)) )]
=1/2 Re[ ( exp( iµ/2(n+2)) -exp( i(2n+1)µ/2(n+2)) /( isin(µ/2(n+2)) )]
=1/2 [ sin(µ/2(n+2)) - sin((2n+1)µ/2(n+2)) ]/ sin(µ/2(n+2))
=cos( (n+1)µ/(n+2))
==> a(n+1)=n+1
Donc qqs n>0, an=n | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mer 08 Aoû 2012, 17:49 Mer 08 Aoû 2012, 17:49 | |
| - Oty a écrit:
- YIRA a écrit:
- Peux-je avoir la solution du 2eme exercice nmo ?
il me semble : que d'apres l'equation initial on a : f(2^x-1)=2^f(x) - 1 => pour x=0 , f(0)=2^f(0) - 1 et pour x=1 f(1)=2^f(1)-1 , ainsi il suffit de montrer que l'equation 2^{x}=x+1 admet seulement deux solution {0 , 1} sur R ce qui permetra de conclure que f(0)+f(1)=1 . (sauf erreur ) http://www.wolframalpha.com/input/?i=2%5Ex%3Dx%2B1 l'equation 2^x=x+1 admit d'autres solutions que (0:1) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  Mer 08 Aoû 2012, 17:54 Mer 08 Aoû 2012, 17:54 | |
| les autres solution sont complexe , deja la courbe de x+1 et de 2^x ce coupe en seulement 2 points ! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Problèmes depuis la Roumanie: Sujet: Re: Problèmes depuis la Roumanie:  | |
| |
|
  | |
| | Problèmes depuis la Roumanie: |  |
|
