Problèmes depuis la Macédonie:

Problème1:
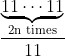
Find all prime numbers of the form , where n is a natural number.
Problème2:
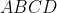
Let the quadruangle be inscribed in a circle of radius 1.
Prove that the difference between its perimeter and the sum of the lengths of its diagonals is positive and less than 4.
Problème3:
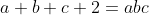
Let a, b and c be positive real numbers for which the equality holds.
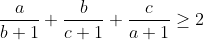
Prove that the inequality holds.
When dos equality holds?
Problème4:
Find all prime numbers p and q which satisfy the equation .
Problème5: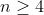
points in the plane are given such that every three of them are nor colinear. Prove that there exists a triangle such that all the points are in its interior, and on each of its sides lies exactly one point of the given points.
Bonne chance.

concernant le probleme 3 , voici
ma solution
posant : a=x-1 , b=y-1 , c=z-1 (avec x,y,z>=1) ,
la condition est equivalente a : xy+yz+zx=xyz .
et l'inégalité est equivalente a :

ce qui est vrai par AM-GM .
egalité si : x=y=z=3 =>a=b=c=2 .