konica
Maître
 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 | | Sujet: Joli problème Sam 01 Sep 2012, 14:43 | |
| Soit ABC un triangle et O le centre de son cercle circonscrit. Les points D,E et F appartiennent respectivement à [BC], [AC] et [AB] tel que (DE) et (OC) sont perpendiculaires et (DF) et (BO) sont perpendiculaires.
Soit K le centre du cercle circonscrit au triangle AFE.
Prouver que (KD) et (BC) sont perpendiculaires. | |
|
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Joli problème Dim 02 Sep 2012, 01:10 | |
|  On note: %20\cap%20(CO)\;%20\;%20\mathrm{et}\;%20\;%20F%27=(FD)\cap%20(BO)) . On a: 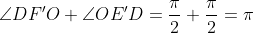 , donc le quadrilatère E'OF'D est inscriptible. Et: 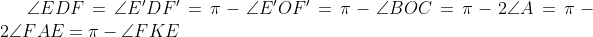 , alors le quadrilatère EDFK est inscriptible. Et puisque 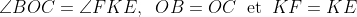 , il s'en suit que les triangle KFE et OBC sont similaires, d'où: angle{KFE}=angle{OCB}. Ainsi:  ... | |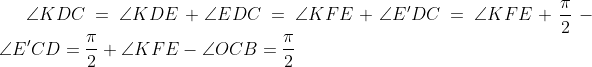
|
