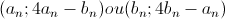Classique mais beau

Soient a et b deux entiers naturels tels que ab divise a²+b²+2.

Prouver que : (a²+b²+2)/ab = 4

salam!
j'ai voulu partager ma solution ,aussi bizarre soit-elle pour comprendre cette méthode que je viens de découvrir .si c'est faux j'aimerais bien avoir une correction pour comprendre

supposons l'existence d'une ou de plusieurs solutions de l'équation (a²+b²+2)/ab =k pour lesquels k=/=4
pour une certaine valeur de k soit (m,n) une solution pour la quelle m+n est minimale et m>=n
remplaçons a par une variable x dans l'équation
donc ²+n²+2-kxn=0
x_1=m est une solution, l'autre solution s'écrit donc _2=(n²+2)/m et on a m/m²+n²+2 donc m/n²+2 et donc x_2 £N* et enfin
m²>=n²>n²+2 donc x_2=(n²+2)/m<m d'où x_2+n<m+n ce qui est contradictoire à la première proposition
d'où la conclusion.

judicecharatein a écrit:

m²>=n²>n²+2 donc ...

c'esi ici la faute n'est ce pas?????

c'est une faute mais on peut l'arranger en écartant le cas m=n il s'ensuit que
[img][/img]
et on conclut .Or, selon ce que je crois la faute se cache ailleurs...

c'est définitive maintenant votre solution est sans erreur...j'ai cru que le delte de l'équations est négative mais il ne l'ai pas d'un certain rang de k,n ( on écarte des cas précis )
je te filicite pour cette sol. pertinente.

Citation :

salam!
j'ai voulu partager ma solution ,aussi bizarre soit-elle pour comprendre cette méthode que je viens de découvrir .si c'est faux j'aimerais bien avoir une correction pour comprendre Smile

supposons l'existence d'une ou de plusieurs solutions de l'équation (a²+b²+2)/ab =k pour lesquels k=/=4
pour une certaine valeur de k soit (m,n) une solution pour la quelle m+n est minimale et m>=n
remplaçons a par une variable x dans l'équation
donc Mad²+n²+2-kxn=0
x_1=m est une solution, l'autre solution s'écrit donc Mad_2=(n²+2)/m et on a m/m²+n²+2 donc m/n²+2 et donc x_2 £N* et enfin
m²>=n²>n²+2 donc x_2=(n²+2)/m<m d'où x_2+n<m+n ce qui est contradictoire à la première proposition
d'où la conclusion.

C'est bien mais c'est incomplet. Voilà une solution, mais elle reste à confirmer.


Solution :

On veut prouver que si a et b sont deux entiers naturels tels que ab divise a²+b²+b alors

Soit :
On fixe k et on considère tous les couples (a,b) qui satisfont l'équation
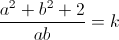
Si a=b alors et en substituant, on trouve k=4 ce qui est vrai.

Maintenant, on suppose que parmi tous les couples , il existe un couple (A,B) pour lequel la somme A+B est minimale dans S. Supposons aussi que

Considérons l'équation
C'est une équation de second degré dont l'inconnu est x.
On A est la première solution de cette équation. Soit
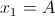
Par les formules de Viète :

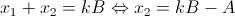
Et :
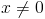
Notons que parce que sinon on aura : ce qui est clairement faux.
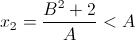
On a : parce qu'elle équivalente à ce qui est vrai.
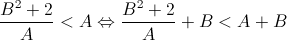
Alors : ce qui est une contradiction avec le fait que la somme A+B est minimale.
Alors A=B, et ce cas nous mène à k=4.
CQFD.

Remarque :
Les couples qui donnent k=4 sont :
(1;1)
(1;3)
(3;1)
(3;11)
(11;3)
(11;41)
.
.
.