Syba
Maître
 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 | | Sujet: derivabilite Mer 31 Oct 2012, 20:12 | |
| Etudier la derivabilité à droite de (-1), de la fonction f définie sur [-1,+oo[, par: f(x)=Arctan[(x³+1)^(1/3)-x]
( le ^(1/3) c'est la racine cubique de (x³+1) ). | |
|
Syba
Maître
Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
| | Sujet: Re: derivabilite Sam 03 Nov 2012, 12:14 | |
| | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: derivabilite Sam 03 Nov 2012, 13:12 | |
| - Syba a écrit:
- Etudier la derivabilité à droite de (-1), de la fonction f définie sur [-1,+oo[, par: f(x)=Arctan[(x³+1)^(1/3)-x]
( le ^(1/3) c'est la racine cubique de (x³+1) ). On a premièrement: =\text{Arctan}(1)=\frac{\pi}{4}) . On s'intéresse donc à la limite suivante: -\frac{\pi}{4}}{x+1}\big)) . On pose ^{\frac{1}{3}}-x) , et puisque 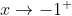 alors 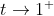 . On peut donc écrire la limite sous la forme -\frac{\pi}{4}}{t-1}\big).\lim_{x\to-1^{+}}\big(\frac{(x^3+1)^{\frac{1}{3}}-x-1}{x+1}\big)) . La première limite vaut  , et la deuxième vaut  . La limite qu'on cherche existe, et elle est infinie. Par conséquent, la fonction  n'est pas dérivable à la droite en -1. Sauf erreurs. | |
|
Syba
Maître
Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
| | Sujet: Re: derivabilite Sam 03 Nov 2012, 14:31 | |
| merci beaucoup pour votre aide précieuse  | |
|
