| | Préparation aux olympiades {2012/2013} |  |
|
+7Wissal El elidrissi Ahmed Taha nmo causchy schwarz 47 Humber legend-crush 11 participants |
|
| Auteur | Message |
|---|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Sam 12 Jan 2013, 23:35 Sam 12 Jan 2013, 23:35 | |
| Exo 2: soit trois cercles de même rayon, trouver un cercle qui soit tangent aux trois cercles | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Sam 12 Jan 2013, 23:38 Sam 12 Jan 2013, 23:38 | |
| Exo 3  (c pas vraiment un olympiade...   ) comparer x et y et z tel que: x+y>=z x+z>=y y+z>=x plz participer au forum !!!!  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 00:18 Dim 13 Jan 2013, 00:18 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 12:58 Dim 13 Jan 2013, 12:58 | |
| - Ahmed Taha a écrit:
- legend-crush a écrit:
- Exo 3
 (c pas vraiment un olympiade... (c pas vraiment un olympiade...   ) )
comparer x et y et z tel que:
x+y>=z
x+z>=y
y+z>=x
plz participer au forum !!!!  mayemkench tratabhom ghir mn had lmo3tayat impossible ah deso j'ai fait une faute Exo 3(c pas vraiment un olympiade... ) comparer x et y et z tel que: x+y>=2z x+z>=2y y+z>=2x | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 13:09 Dim 13 Jan 2013, 13:09 | |
|
Dernière édition par legend-crush le Dim 13 Jan 2013, 13:34, édité 1 fois | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 13:11 Dim 13 Jan 2013, 13:11 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 13:35 Dim 13 Jan 2013, 13:35 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 23:07 Dim 13 Jan 2013, 23:07 | |
| EXO 4[img]  [/img] | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 13 Jan 2013, 23:11 Dim 13 Jan 2013, 23:11 | |
|
Dernière édition par legend-crush le Mer 30 Avr 2014, 14:11, édité 1 fois | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Lun 14 Jan 2013, 19:34 Lun 14 Jan 2013, 19:34 | |
|
Dernière édition par legend-crush le Mer 30 Avr 2014, 14:10, édité 1 fois | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Lun 14 Jan 2013, 19:56 Lun 14 Jan 2013, 19:56 | |
| A vous!! PArticipez s'il vous plait!! Exo 1: 1 000 000 000 000 000 000 001 est il premier??!
Exo 2: trouver un polynome a coefficients entier et qui est comme racine:  Exo3 : Exo3 : soit x et y des réels positif tel que x+y=1. montrer que (1+(1/x))(1+(1/y))>=9 Exo 4: (x^4)+4(y^4) est-il premier?!
Je Posterai les solutions dans 2 ou 3 jours! Allez a vous de jouer
| |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Mar 15 Jan 2013, 15:02 Mar 15 Jan 2013, 15:02 | |
| - legend-crush a écrit:
- A vous!! PArticipez s'il vous plait!!
Exo 1: 1 000 000 000 000 000 000 001 est il premier??!
Exo 2: trouver un polynome a coefficients entier et qui est comme racine:
Exo3 : soit x et y des réels positif tel que x+y=1.
montrer que (1+(1/x))(1+(1/y))>=9
Exo 4: (x^4)+4(y^4) est-il premier?!
Je Posterai les solutions dans 2 ou 3 jours! Allez a vous de jouer
Exo 1 (10^{14}-10^7+1)) Exo 2 voir ce lien : http://www.wolframalpha.com/input/?i=%5Csqrt%7B2%7D%2B%5Csqrt%5B3%5D%7B3%7D Exo 3 \left&space;(&space;1+\frac{1}{y}&space;\right&space;)\geq&space;9\Leftrightarrow\left&space;\left&space;(&space;2+\frac{y}{x}&space;\right&space;)(&space;2+\frac{x}{y}&space;\right&space;)\geq&space;9&space;\\\Leftrightarrow&space;5+2\left&space;(\frac{y}{x}+\frac{x}{y}&space;\right&space;)\geq&space;9&space;\Leftrightarrow&space;\frac{y}{x}+\frac{x}{y}\geq&space;2&space;\&space;\&space;\&space;(AM-GM)) Exo 4 (x^2+2xy+2y^2)) | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Mar 15 Jan 2013, 15:22 Mar 15 Jan 2013, 15:22 | |
| Exo 43 (x^4+x^2+1)+1\geq&space;x^2-x+1\geq&space;\frac{3}{4}%3E&space;\frac{1}{2}) Exo 45 Par HOLDER : ^2}{a+1+b+1}=\frac{1}{3}) | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Mar 15 Jan 2013, 19:48 Mar 15 Jan 2013, 19:48 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Mar 15 Jan 2013, 22:43 Mar 15 Jan 2013, 22:43 | |
| Al6 c facile je crois donc je donne la solution (si c juste)!! poster vos resultats pour les autres exos: 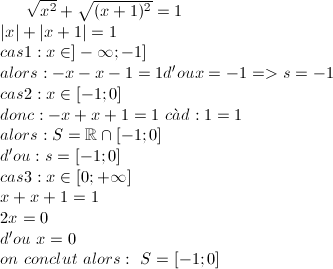 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Mer 16 Jan 2013, 19:05 Mer 16 Jan 2013, 19:05 | |
| je poste les exos tous seul et je poste les solution tous seul!! participez voyons!! | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 20 Jan 2013, 01:31 Dim 20 Jan 2013, 01:31 | |
| salam
cest faut je crois
-0.5 est un contre exemple
la solution est [0,1]
Dernière édition par elidrissi le Dim 20 Jan 2013, 10:44, édité 2 fois | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 20 Jan 2013, 02:01 Dim 20 Jan 2013, 02:01 | |
| quote="legend-crush"] - legend-crush a écrit:
[img] [/img] [/img]
Voici la solution!!! cliquez sur le spoiler; essayez tout de meme avant de voir      : :- Spoiler:
[img]  [/img]
[/quote] salut c'est juste, mais ce n'est pas complet, il se peux que "l Assas" soit égal a -1 et que la puissance soit paire (positive ou négative peut importe) j'essayerais de poster la solution complete quand j'aurais le temps ^^
Dernière édition par elidrissi le Dim 20 Jan 2013, 11:06, édité 1 fois | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Dim 20 Jan 2013, 13:12 Dim 20 Jan 2013, 13:12 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Ven 01 Fév 2013, 13:29 Ven 01 Fév 2013, 13:29 | |
| | |
|
  | |
Wissal El
Féru

 Nombre de messages : 62 Nombre de messages : 62
Age : 27
Localisation : Sefrou
Date d'inscription : 16/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Ven 01 Fév 2013, 16:29 Ven 01 Fév 2013, 16:29 | |
| Salut Svp j n'arrive pas à comprendre ce passage  a²+b²+c²+2b(a+c)+2ac<1 ==> a²+b²+c²-2b-2a<1 Expliquez-le moi svp  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Sam 02 Fév 2013, 00:18 Sam 02 Fév 2013, 00:18 | |
| - Humber a écrit:
- 1)
Remplacer x par 0
2) remplacer x par 1 puis par -1 et sommer
3)
|a+b+c| < 1 ==> a²+b²+c²+2ab+2bc+2ac<1 ==> a²+b²+c²+2b(a+c)+2ac<1 ==> a²+b²+c²-2b-2a<1 ==> a²+b²+c² <2(a+b)+1
Il suffit de montrer que a+b <2
(-1<a+b+c < 1 avec -1<-c<1) ==> |a+b|<2 CQFD oui, je crois que pour que tu puisse paasser de a²+b²+c²+2b(a+c)+2ac<1 à a²+b²+c²-2b-2a<1 il faut que c>a>0 - Citation :
- Salut
Svp j n'arrive pas à comprendre ce passage
a²+b²+c²+2b(a+c)+2ac<1 ==> a²+b²+c²-2b-2a<1
Expliquez-le moi svp si (et je dis bien "si") j'ai bien compris, a²+b²+c²+2b(a+c)+2ac<1, on a -2ac-2bc-2ab<0, en sommant, on a a²+b²+c²<1 , puis la meme chose, mais dans ce cas là, ce serais si et seulement si c,a >0 | |
|
  | |
aminesm
Féru
 Nombre de messages : 60 Nombre de messages : 60
Age : 26
Localisation : rabat
Date d'inscription : 25/02/2014
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Ven 28 Fév 2014, 00:57 Ven 28 Fév 2014, 00:57 | |
| legend-crush t'es en quel niveau? | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Ven 28 Fév 2014, 09:05 Ven 28 Fév 2014, 09:05 | |
| Je suis, comme elidrissi et LWP et sketshup, en 1ière année Bac | |
|
  | |
Bovlmakovl
Habitué
 Nombre de messages : 18 Nombre de messages : 18
Age : 29
Date d'inscription : 26/08/2013
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  Ven 28 Fév 2014, 11:34 Ven 28 Fév 2014, 11:34 | |
| Bonjour, J'ai déja passé les stages de l'IMO a rabat vers la fin de mon année de terminale, et je m'y connais un peu. Pour aider ceux ou celles qui comptent préparer les IMO, je conseille de savoir qqs petits trucs: * pour les inégalités, il faudrait au moins connaitre : - l'inégalité du réordonnement - l'inégalité de tchebychev - l'inégalité de la moyenne ( harmonique, géometrique, arithmétique et quadratique ) - l'inégalité de Cauchy shwartz ( très utile puisqu'elle fourni un cas d'égalité) - l'inégalité triangulaire ( bien sur ) - l'inégalité de jensen ( ou de convexité ) - l'inégalité de schur (moins souvent rencontrée, mais utile des fois ) * des notions sur l'arithmétique des polynomes * des notions sur l'arithmétique dans Z (théo d'eulern de fermat, algorithme d'euclide, théorème chinois, notions sur les équations diophantiennes... ) *des principes généraux ( le principe des tiroirs, la récurrence simple et forte, la descente infinie, principe des invariants... ) * et puis un bon bagage de théorème de géométrie  Je sais qu'a votre niveau c po évident de maitriser tout ça, mais faites un petit effort, c po si compliqué, surtout durant l'été, ne perdez pas trop de temps. pour des ressources documentaires, vous pouvez chercher le livre " Tarik Belhajj Soulami" qui est très très intéressant, ou voir sur le site de l'association animath ou vous trouverez des cours et plein de trucs utiles. une autre chose, les épreuves qu'on vous propose en première bac ne sont pas suffisantes ( elles sont trop faciles au fait pr le niveau exigé par les IMO :p ) BONNE CHANCE a tous  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation aux olympiades {2012/2013} Sujet: Re: Préparation aux olympiades {2012/2013}  | |
| |
|
  | |
| | Préparation aux olympiades {2012/2013} |  |
|
