radouane_BNE
Modérateur
 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 | | Sujet: deux inégalités avec les complexes Mar 08 Jan 2013, 22:16 | |
| soit z un complexe et a et b deux réels tels que -1<a,b<1. Montrer que : et : | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: deux inégalités avec les complexes Jeu 24 Jan 2013, 18:50 | |
| - radouane_BNE a écrit:
- soit z un complexe et a et b deux réels tels que -1<a,b<1.
Montrer que :
On a (1-ab)}{(1-az)(1-bz)}\Bigg|=\Bigg|\frac{1-ab-z^2+abz^2+z(a+b)-z(a+b)}{(1-az)(1-bz)}\Bigg|=\Bigg|\frac{(1-az)(1-bz)-(z-a)(z-b)}{(1-az)(1-bz)}\Bigg|) . Et par l'inégalité triangulaire: (1-ab)}{(1-az)(1-bz)}\Bigg|\le\Bigg|\frac{(1-az)(1-bz)}{(1-az)(1-bz)}\Bigg|+\Bigg|\frac{-(z-a)(z-b)}{(1-az)(1-bz)}\Bigg|=1+\Bigg|\frac{(z-a)(z-b)}{(1-az)(1-bz)}\Bigg|) . Il suffit donc de démontrer:  .==>(*) Posons pour cela 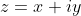 . L'inégalité * devient: ^2+y^2}\le\sqrt{(1-ax)^2+(ay)^2}) , ou encore ^2+(ay)^2}) soit (x^2+y^2-1)) . Cela est vrai, car 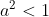 et 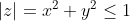 . De même, on démontre que 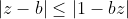 et ainsi (z-b)}{(1-az)(1-bz)}\Bigg|\le1) . D'où: (1-ab)}{(1-az)(1-bz)}\Bigg|\le1+1=2) , soit (1-bz)}\Bigg|\le\frac{2}{1-ab}) . L'égalité aura lieu si et seulement si 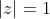 (d'après l'inégalité *). CQFD. Sauf erreurs. | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: deux inégalités avec les complexes Jeu 24 Jan 2013, 18:54 | |
| | |
|
younesmath2012
Expert sup
Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
| | Sujet: Re: deux inégalités avec les complexes Jeu 24 Jan 2013, 20:05 | |
| | |
|
Contenu sponsorisé
| | Sujet: Re: deux inégalités avec les complexes | |
| |
|
