| | Marathon d'arithmetique |  |
|
+6Vz nmo elidrissi alidos aymas galillee56 10 participants |
|
| Auteur | Message |
|---|
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Marathon d'arithmetique Sujet: Marathon d'arithmetique  Lun 24 Juin 2013, 16:54 Lun 24 Juin 2013, 16:54 | |
| il y a des marathons partout ces derniers temps grace a plusieurs personne passione de maths sur ce site ca fait plaisir de voir ca  .donc voici un marathons d'arithmetiques les regles sont les meme bon marathons exo 1:
trouver a et b tel que 3^a+7^b soit un carre parfait. | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 17:54 Lun 24 Juin 2013, 17:54 | |
| Solution pour exercice 1- Spoiler:
| |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 18:02 Lun 24 Juin 2013, 18:02 | |
| bien joue  a vous de poser un exo | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 18:06 Lun 24 Juin 2013, 18:06 | |
| Exercice 2 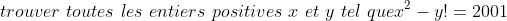 | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 18:32 Lun 24 Juin 2013, 18:32 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 18:38 Lun 24 Juin 2013, 18:38 | |
| Mr Galille56
Pour quoi si 9 divise y! alors il divise 2001
Afin que ca soit vrai il faut au moins que 3 divise x ce qui n'est pas forcement vrai.
Mais on tout cas tu est sur le bon chemain | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 19:03 Lun 24 Juin 2013, 19:03 | |
| si si c bon car si 3<y 3/x^2 donc 3|x donc 9|x^2  j'ai oublie de le preciser merci  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Juin 2013, 19:36 Lun 24 Juin 2013, 19:36 | |
| exo 3: soit a et n des entier positif prouver que : 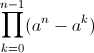 est divisible par n! | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 06 Juil 2013, 21:14 Sam 06 Juil 2013, 21:14 | |
| voici ce que je propose - Spoiler:
si a^i=1 il existe 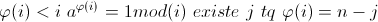 donc si a^i=1 i divise  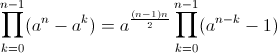 si p est dans [1,n] sa valuation p a-dique est plus petite que n(n-1)/2 donc si a^i=d i=i'd i'\a^(n-j)-1 d divise a^(n(n-1)/2)
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 06 Juil 2013, 21:18 Sam 06 Juil 2013, 21:18 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 06 Juil 2013, 21:24 Sam 06 Juil 2013, 21:24 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Mar 09 Juil 2013, 17:31 Mar 09 Juil 2013, 17:31 | |
| Je vous propose l'exo suivant (edite pour ne pas bloque se marathon)
Exo 4
Trouver toutes les entiers tel que 2^{a}+3^{b}=5^{c} | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Ven 12 Juil 2013, 12:17 Ven 12 Juil 2013, 12:17 | |
| Salut Aymane  bon je propose une solution - Spoiler:
2^{a}+3^{b}=5^{c}
- si a=0 alors
1+3^{b}=5^{c}
on a 3^{b}=0(mod 4)
d'ou la contradiction
- si b=0 alors
2^{a}+1=5^{c}
si c>=2 clairement on a a>=3
ainsi 5^{c}=1(mod 8.)ainsi c est pair
d'autre part on a 5^{c}=1(mod 3)
ainsi 2^{a}=0(mod 3)
ainsi c=<1
si c=1 alors on a a=2
si c=0 alors pas de solutions
- si c=0 clairement pas de solutions
- si (a,b,c)£ IN*
on a 2^{a}+3^{b} =5^{c}
si a=2 alors
4+3^{b} =5^{c}
on a 5^{c}=1(mod 3) ainsi c est pair
de meme 3^{b}=1(mod 4) ainsi b est pair
comme b est pair on a 3^{b} =1(mod 8.)
ainsi 5^{c}=5(mod 8.)contradiction avec la parité de c
si a>=3
on a 3^{b}=1(mod 4) ainsi b est pair
ainsi comme b est pair et a>=3 on a 5^{c}=1(mod 8.)
ainsi c est pair
notons c=2u et b=2v avec (u,v)£ IN*
on a (5^{u}-3^{v} )(5^{u}+3^{v}} = 2^{a}
selon la parité de v et en passant par le modulo 4
l'un d'eux doit étre égal à 2
dans les deux cas on aura 2.5^{u}=2+2^{a-1}
ainsi 5^{u} =1+2^{a-2}
qui n'est que l'équation du cas ou b=0 ainsi a=4 et b=2,c=2
il nous reste qu'a traiter le cas ou a=1
ou on aura
2+3^{b}=5^{c}
1+3^{b} =5^{c}-1
ainsi v_2 (b) +2 = v_2(c)+2
ainsi v_2(b)=v_2(c) =x
supposons que x>0
alors b=2^{x}.d avec pgcd(d,2)=1
récrivons l'équation initiale sous forme de
5^{c}-5 = 3^{b}-3
ainsi 5(5^{c-1}-1) =3(3^{b-1}-1)
ainsi 5| 3^{2^{x}.d -1} -1
on connait que si 5|3^{n}-1 alors 4|n
ainsi 4|2^{x}.d -1 absurde ainsi
b=1 et en reprochant à l'équation initiale on a c=1
finalement l'ensemble des solutions est
S={(1.1.1) , (2.0.1) ,(4,2,2) }
Dernière édition par alidos le Ven 12 Juil 2013, 13:32, édité 2 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Ven 12 Juil 2013, 12:30 Ven 12 Juil 2013, 12:30 | |
| Exercice 5soit a,b,x des entiers naturelles tels que  prouver que 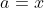 et 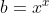 | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Dim 14 Juil 2013, 14:39 Dim 14 Juil 2013, 14:39 | |
| salut les matheux, ça va? pour lexo d alidos je me suis concentré sur x étant premier, pour x n'étant pas premier ce sera plus ou moins la memechose - Spoiler:
dabord on a: b>0 et a>0 (parcequ ils sont des puissances de x)
soit k et n 2 entiers naturels tel que a=x^k et b=x^n
x^(a+b)=x^(kb).x^n =x^(kb+n) donc a+b=kb+n
b(k-1)=a-n
pour k=0 :-b=a-n <==> b=n-a <==> b=n-x^n <0 ce qui est contradictoire (b>0)
pour k>=1
pour k=#=1
a+b=kb+n <==>a-n=k(b-1) >=0
b>=a donc n>=k
(k-1) x^n=x^k -n
k-1=(x^k -n)/x^n
k<=n donc (x^k -n)/x^n nest pas un entier, contradiction
donc k=1
pour k=1, k-1=0 donc a-x=0 donc a=x
donc a=x=n, et donc a=x
en remplacant on trouve (k-1) x^n =n-x=0 donc x=n=a donc a=x et b=x^x
sauf erreur biensur ^w^ ze sais ze sais, zai mis beaucoup de cas :p
Dernière édition par elidrissi le Dim 14 Juil 2013, 21:56, édité 3 fois | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Dim 14 Juil 2013, 18:16 Dim 14 Juil 2013, 18:16 | |
| voila, la generalisation
soit A B et X des nombres tels que
X^(A+B)=B. A^B
on pose X=c.x ,A=a. x^k et B=b. x^n tel que x est un nombre premier et a et b nadmettent pas la division sur x
pour que cela se réalise, il faut que les puissances des x des 2 cotées soit égales, donc:
x^(A+B)=x^(k+B) . x^n
donc A+B=kB+n , equation déja résolue ( la methode est un tout petit peu differente, mais je vais pas la mettre)
pour que cela soit vrai , ces valeurs k=1 ,n= X=A et B=X^X doivent réaliser c^(A+B)=b. a^B
on a X=A donc c.x=a.x^k donc c=a. x^(k-1)=a.x^(1-1)=a donc c=a
donc a^(A+B)=b. a^B donc b =a^B
en remplacant au tout début et en simplifiant on obtient (ax)^X=b. x^X donc b=x^X , ce qui réalise ce qui est demandé
sauf erreur | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Ven 19 Juil 2013, 00:36 Ven 19 Juil 2013, 00:36 | |
| - elidrissi a écrit:
- voila, la generalisation
soit A B et X des nombres tels que
X^(A+B)=B. A^B
on pose X=c.x ,A=a. x^k et B=b. x^n tel que x est un nombre premier et a et b nadmettent pas la division sur x
pour que cela se réalise, il faut que les puissances des x des 2 cotées soit égales, donc:
x^(A+B)=x^(k+B) . x^n
donc A+B=kB+n , equation déja résolue ( la methode est un tout petit peu differente, mais je vais pas la mettre)
pour que cela soit vrai , ces valeurs k=1 ,n= X=A et B=X^X doivent réaliser c^(A+B)=b. a^B
on a X=A donc c.x=a.x^k donc c=a. x^(k-1)=a.x^(1-1)=a donc c=a
donc a^(A+B)=b. a^B donc b =a^B
en remplacant au tout début et en simplifiant on obtient (ax)^X=b. x^X donc b=x^X , ce qui réalise ce qui est demandé
sauf erreur L'équation diophantienne que tu as trouvé admet une infinité de solutions. Je pense qu'il te faut plus d'argument pour aboutir à k=1. De plus, je ne vois pas comment tu as fait pour conclure que n=X=A!! (En admettant que tu as eu k=1, tu n'aura que A=a). | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Dim 28 Juil 2013, 21:58 Dim 28 Juil 2013, 21:58 | |
| bonsoir, lis le post davant stp. cest en prenant x premier, la cest un peu different mais cest a peu pres la meme chose pour ce passage en rouge  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 29 Juil 2013, 21:56 Lun 29 Juil 2013, 21:56 | |
| - elidrissi a écrit:
- bonsoir, lis le post davant stp. cest en prenant x premier, la cest un peu different mais cest a peu pres la meme chose pour ce passage en rouge
 Ce n'est pas la même chose. Aucune particularité n'est donnée aux entiers vérifiant l'équation: A+B=k.B+n. Et voici un contre exemple: 8+5=2.5+3 (A=8, B=5, k=2 et n=3). Il faut changer d'optique... | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Mar 30 Juil 2013, 17:27 Mar 30 Juil 2013, 17:27 | |
| - alidos a écrit:
- Exercice 5
soit a,b,x des entiers naturelles tels que

prouver que 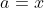 et et 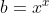
Dans la suite on notera  la valuation p-adique de la valuation p-adique de  , on introduit aussi le petit lemme suivant qui nous servira à plusieurs reprises dans la démonstration :si , on introduit aussi le petit lemme suivant qui nous servira à plusieurs reprises dans la démonstration :si  est un entier naturel non nul alors pour tout nombre premier est un entier naturel non nul alors pour tout nombre premier  on a on a  Maintenant on commencera par supposer que les entiers Maintenant on commencera par supposer que les entiers  et et  sont non nuls sans quoi le problème devient immédiat, on a donc pour tout nombre premier sont non nuls sans quoi le problème devient immédiat, on a donc pour tout nombre premier  l'égalité l'égalité  , une bonne première chose est de poser , une bonne première chose est de poser  si bien que l'on peut trouver deux entiers si bien que l'on peut trouver deux entiers  et et  premiers entre eux tels que premiers entre eux tels que  et et  , l'égalité devient , l'égalité devient  , donc il est clair que , donc il est clair que  est un diviseur de est un diviseur de  et comme cela vaut pour tout nombre premier et comme cela vaut pour tout nombre premier  on peut écrire on peut écrire  pour un certain entier naturel pour un certain entier naturel  , supposons dans un premier temps que , supposons dans un premier temps que  et soit un diviseur premier et soit un diviseur premier  de de  , montrons que ce choix implique , montrons que ce choix implique  , si tel n'était pas le cas alors , si tel n'était pas le cas alors  et comme on a déjà montré que et comme on a déjà montré que  alors on a nécessairement alors on a nécessairement  donc en écrivant donc en écrivant  on voit bien que on voit bien que  cela contredit le fait que cela contredit le fait que  de manière similaire on peut remarquer que de manière similaire on peut remarquer que  . Or l'équation peut s'écrire aussi de la forme . Or l'équation peut s'écrire aussi de la forme  avec un tel choix du nombre premier avec un tel choix du nombre premier  on doit avoir on doit avoir  , et comme , et comme  alors alors  et donc et donc  d'après le lemme ce qui est absurde. On vient donc de montrer que d'après le lemme ce qui est absurde. On vient donc de montrer que  , si , si  on obtient facilement on obtient facilement  sinon l'égalité sinon l'égalité  montre que montre que  , or l'inégalité de la moyenne arithmérique géométrique donne: , or l'inégalité de la moyenne arithmérique géométrique donne:  et donc et donc  d'autre part on a évidemment d'autre part on a évidemment  car sinon on aura car sinon on aura  ce qui est faux, ainsi pour tout diviseur premier ce qui est faux, ainsi pour tout diviseur premier  de de  on a on a  donc on a nécessairement donc on a nécessairement  pour tout diviseur premier pour tout diviseur premier  de de  comme cela est clairement vrai aussi pour comme cela est clairement vrai aussi pour  on a donc on a donc  et et  cela permet de conclure cela permet de conclure  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 | |
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 22 Fév 2014, 10:43 Sam 22 Fév 2014, 10:43 | |
| Pourquoi ne pas reprendre Ce sujet d'Arithmétique? vu que il ya eu un marathon d'inegalités un autre d'EF et un petit troisième de géométrie.
Les règles sont claires: qui résoud un exercice (en Spoiler) en poste un nouveau.
Exercice 6:
Montrer que si 2^n − 1 est un nombre premier, alors n est également premier. | |
|
  | |
Freud.
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Localisation : Casablanca
Date d'inscription : 22/02/2014
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 22 Fév 2014, 11:17 Sam 22 Fév 2014, 11:17 | |
| - Solution 6:
Supposons que n soit composé et que d soit un diviseur strict de n
On peut donc écrire n=dd' et
(2^n-1)=(2^d-1)(2^d(d'-1)+2^d(d'-2)+....+1)
alors le facteur 2^d-1 est non trivial et donc 2^n-1 est composé d'où
dsl pr cette écriture ,mon latex n'est pas available
N.B les nombres de la forme 2^p-1 où p est un nombre premier sont appelés nombres de Mersenne | |
|
  | |
Freud.
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Localisation : Casablanca
Date d'inscription : 22/02/2014
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Sam 22 Fév 2014, 11:19 Sam 22 Fév 2014, 11:19 | |
| Exercice 7
Pour quelles valeurs de a l'équation x²+axy+y²=1 admet-elle un infinité de solutions dans Z ? | |
|
  | |
Lonely-Guy
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Date d'inscription : 23/02/2014
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  Lun 24 Fév 2014, 08:25 Lun 24 Fév 2014, 08:25 | |
| Signe:
On remarque que x=1 y=-a est toujours solution de l'équation | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon d'arithmetique Sujet: Re: Marathon d'arithmetique  | |
| |
|
  | |
| | Marathon d'arithmetique |  |
|
