| | jolie inegalite |  |
|
|
| Auteur | Message |
|---|
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: jolie inegalite Sujet: jolie inegalite  Sam 28 Déc 2013, 14:41 Sam 28 Déc 2013, 14:41 | |
| Soient a.b.c et d trois reels positifs tel que
(1/1+a^2)+(1/1+b^2)+(1/1+c^2)+(1/1+d^2)=1
M.Q: abcd>ou=3
Merci d'avance pour les reponses ! | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Ven 03 Jan 2014, 20:20 Ven 03 Jan 2014, 20:20 | |
|
Dernière édition par aymas le Ven 03 Jan 2014, 20:21, édité 1 fois | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 17:38 Sam 04 Jan 2014, 17:38 | |
| Ya une erreur dans la question ^^ c'est ou bien  | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 20:00 Sam 04 Jan 2014, 20:00 | |
| J'ajoute une autre Soit a,b,c >0 tels que abc=1 M.Q: (a-1+1/b)(b-1+1/c)(c-1+1/a)<ou= 1 SVP n'hesitez pas  Et Merci d'avance !!! | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 20:29 Sam 04 Jan 2014, 20:29 | |
| - indication:
pose a=x/y et b=y/z et c=z/x .c'est l'inegalite de schur.
| |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 20:53 Sam 04 Jan 2014, 20:53 | |
| - bianco verde a écrit:
- J'ajoute une autre
Soit a,b,c >0 tels que abc=1
M.Q: (a-1+1/b)(b-1+1/c)(c-1+1/a)<ou= 1
SVP n'hesitez pas 
Et Merci d'avance !!! prend a=x/y , b=y/z et c=z/x (abc=1) alors 1≥(a-1+1/b)(b-1+1/c)(c-1+1/a) => xyz≥(x+y-z)(x+z-y)(y+z-x) <=> x^3+y^3+z^3+3xyz≥ x²y+x²z+xy²+y²z+xz²+yz² ce qui vrai par Schur (le cas t=1) | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:00 Sam 04 Jan 2014, 21:00 | |
|
Voyez comme je suis nouveau ; pouvez vous m'expliquer l'inegalité de Schür .?
Et Merci d'Avance...
| |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:13 Sam 04 Jan 2014, 21:13 | |
| - bianco verde a écrit:
Voyez comme je suis nouveau ; pouvez vous m'expliquer l'inegalité de Schür .?
Et Merci d'Avance... aah bon l'inégalité de Schur : 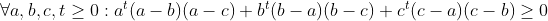 avec égalité si et seulement si a, b, c sont égaux ou si deux d'entre eux sont égaux et le troisième est nul. dans le cas t=1 on obtient : 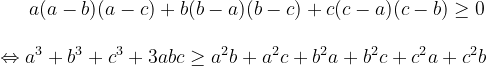
Dernière édition par Ahmed Taha le Sam 04 Jan 2014, 21:16, édité 1 fois | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:15 Sam 04 Jan 2014, 21:15 | |
| Ça y est je viens de comprendre l'inegalite de Schür / Tout est clair maintenant ; je vous remercie  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 | |
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:20 Sam 04 Jan 2014, 21:20 | |
| J'ajoute une autre
Soit x,y et z > 0
Tels que xyz>=xy+xz+yz
Prouver que xyz>=3(x+y+z)
Amicalement ^^ | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:33 Sam 04 Jan 2014, 21:33 | |
| Par Schur on a
x^3+y^3+z^3-3xyz>=x(z^2+y^2)+z(x^2+y^2)+y(x^2+z^2)
Donc x^3+y^3+z^3-3xyz>=x(z-y)^2+z(x-y) | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:36 Sam 04 Jan 2014, 21:36 | |
| Je continue dsl
x^3+y^3+z^3>=x(z-y)^2+z(x-y)^2+y(x-z)^2>=0
D'ou le resultat voulu .
Merci les gars la methode Schur est terriblement efficace
| |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:38 Sam 04 Jan 2014, 21:38 | |
| Faute de frappe dans le prmier msg
! Dsl ! | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:55 Sam 04 Jan 2014, 21:55 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  Sam 04 Jan 2014, 21:58 Sam 04 Jan 2014, 21:58 | |
| - bianco verde a écrit:
- J'ajoute une autre
Soit x,y et z > 0
Tels que xyz>=xy+xz+yz
Prouver que xyz>=3(x+y+z)
Amicalement ^^ 1) l'inégalité AM-GM (moyenne arithmétique et moyenne géométrique) 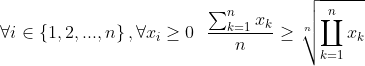 supposons a=1/x ,b=1/y et c=1/z alors 1≥a+b+c donc il faut démontrer : 1/3≥ab+ac+bc aprés AM-GM 2ab≥a²+b² , 2ac≥a²+c² et 2bc≥b²+c² donc 1≥(a+b+c)²≥3(ab+ac+bc) d'où 1/3≥ab+ac+bc | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: jolie inegalite Sujet: Re: jolie inegalite  | |
| |
|
  | |
| | jolie inegalite |  |
|
