| | 4eme olympiade pour 1ères |  |
|
+8elmrini Nas8 seledeur Sketshup bianco verde L-W-P legend-crush elidrissi 12 participants |
|
| alors combien d exercices avez-vous resolus? | | 1 exercice | | 14% | [ 1 ] | | 2 exercices | | 0% | [ 0 ] | | 3 exercices | | 86% | [ 6 ] |
| | Total des votes : 7 | | | |
|
| Auteur | Message |
|---|
ipek
Habitué

 Nombre de messages : 26 Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 17:16 Dim 23 Fév 2014, 17:16 | |
| je pense qu'il mérite une semaine :p comment avez vous résolu le 2éme exercice !! leçon du dénombrement non!? | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 20:54 Dim 23 Fév 2014, 20:54 | |
| Pour ma méthode du deuxième:
-Oublier le nombre 2013, qui n'est qu'un exemple lambda, et considérer le problème en sa généralité. ça veut dire trouver le nombre de triplets (x;y;z) naturels ET non nuls f(m), de sorte que x + y + z = m, avec m, évidemment, supérieur ou égal à 3.
-Découvrons un peu la fonction f. Pour cela, prendre de petites valeurs pour m, commençons par 3, pour ne remarquer qu'un triplet, puis passer à 5, à 8, à 9. L'astuce pour les trouver "méthodiquement", et de fixer x à une colonne verticale, puis augmenter de 1 à chaque colonne horizontale y, puis en déduire z.
-On remarque que ce nombre de triplets forme un triangle dont la forme est semblable au triangle de Pascal: C'est un triangle qui retourne le nombre de triplets selon la relation suivante (Si je me souviens bien, sauf faute de mémoire): (m-1)(m-2)/2.
N.B: On devine cette relation par la sommation suivante: 1 + 2 + ... + (m-2), le décalage de 2 par m est expliqué par le fait que x et y, que l'on choisit, sont non nuls.
-Maintenant, on a notre fonction: f(m) = (m-1)(m-2)/2. Mais nous ne sommes encore qu'à l'hypothèse. Essayons de démontrer par de la rédaction cette hypothèse. J'ai procédé par récurrence: La propriété est valable pour m = 3, le nombre minimal, supposons que ça l'est pour un certain m, et démontrons que c'est vrai pour un certain m+1.
x+y+z = m <=> x + y + z + 1 = m + 1 <=> (x+1) + y + z = m + 1. Ceci implique une rangée horizontale de plus dans notre triangle qui modélise l'exercice, une rangée dont le nombre d'éléments est de (m - 1) [N'oubliez pas le décalage de 2!], s'ajoutera donc m-1 solutions pour m+1. Donc: f(m+1) = f(m) + m + 1 = m(m-1)/2. Ce qui confirme l'hypothèse.
Propriété: Le nombre de triplets d'entiers naturels non nuls solutions de l'équations x + y + z = m, est (m-1)(m-2)/2.
L'exercice pose la question pour m = 2013, on remplace, et on conclut!
Question qui m'est venue à l'instant (et petit défi pour les intéressés...): Ajoutons le paramètre n-uplets dans l'exercice pour bien traiter le sujet.
Trouver le nombre de n-uplets d'entiers naturels non nuls en fonction de n et de m, solutions de l'équation diophantienne SOMME DES UPLETS = m (m>= n évidemment). | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 21:19 Dim 23 Fév 2014, 21:19 | |
| ma methode :
l equation a+b=x a c-1 solution en N*
a+b+c=m <==>a+b=m-c
pour chaque valeur de c il ya m-c-1 solution. il suffit de faire la somme ^^
pour generaliser c est la memechose.
| |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 21:21 Dim 23 Fév 2014, 21:21 | |
| Le nombre de n-uplets solutions de l'équation: x_1+x_2+...+x_n=m est 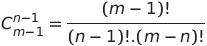 En prenant m=2013 et n=3, on trouve 2012!/[2!.2011!] =2011.2012/2 | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 21:45 Dim 23 Fév 2014, 21:45 | |
| L-C: Peux-tu le démontrer? | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Dim 23 Fév 2014, 22:02 Dim 23 Fév 2014, 22:02 | |
| Si on considère un segment avec les valeur 1, 2, ...,m. il faut trouver le nombre de façon avec lequels on peux poser n-1 point incarnant les nombres x_1, x_2 ...x_n , dans m-1 place . ce qui permet de déduire l'expression... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Lun 24 Fév 2014, 10:28 Lun 24 Fév 2014, 10:28 | |
| - elidrissi a écrit:
- le 3:
ABCD est un quadrillatere convexe tel que : AB+CD=6 et AD+BC=8.
calculer la surface maximale de ABCD. quand ABCD l'atteint il? On utilise la formule de Brahmagupta: (p-CD)(p-AD)(p-BC)}) . Où =7) . Ainsi: (-7+AD.BC)}) . Et, on a selon l'inégalité arithmético-géométrique: ^2=9) avec égalité si et seulement si 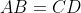 . De même: ^2=16) avec égalité si et seulement si 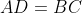 . Ce qui donne: (-7+AD.BC)}\le\sqrt{16\times9}=12) . Dans les conditions d'égalité, les deux triangles  et 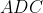 sont égaux. Ils ont par conséquent la même surface, et donc la demi surface du quadrilatère 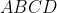 . Cela se traduit par: 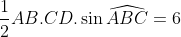 ou encore 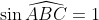 ; et il s'agit d'un angle droit. Le même raisonnement conduit à ce que tous les angles du quadrilatère sont orthogonaux. Par conséquent, le quadrilatère satisfaisant l'égalité est un rectangle. Sauf erreurs. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Lun 24 Fév 2014, 11:19 Lun 24 Fév 2014, 11:19 | |
| | |
|
  | |
*youness*
Maître

 Nombre de messages : 132 Nombre de messages : 132
Date d'inscription : 16/08/2011
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Lun 24 Fév 2014, 13:03 Lun 24 Fév 2014, 13:03 | |
| On considère un segment [A(0),A(n)] de longueur n, Toute solution dans (lN*)^{m} de l'équation équivaut au choix de m-1 points B(1),...,B(m-1) parmi les points A(1),...,A(n-1) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  Lun 24 Fév 2014, 18:53 Lun 24 Fév 2014, 18:53 | |
| - legend-crush a écrit:
- La formule de Brahmagupta est pour les quadrilatère convexes et inscriptibles
Oui, tu as raison, je l'ai oublié. Ma solution est ainsi fausse, sauf si on démontre que parmi les quadrilatères qui ont le même périmètre ce sont ceux inscriptibles qui ont une surface maximale... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: 4eme olympiade pour 1ères Sujet: Re: 4eme olympiade pour 1ères  | |
| |
|
  | |
| | 4eme olympiade pour 1ères |  |
|
