JEU D'ÉTÉ 2014 .

Voila; que chacun se sente libre de participer ! Les regles sont bien connues ( surtout numérotez les exos )

EXERCICE 1:     Résoudre l'equation diophantienne suivante   x^2-2y^4=1

A Vos Stylos

Entiers naturels ! Dsl !

EXERCICE 1

Spoiler:

si c est correct je propose de commencer avec un peu de combi
exercice 2
pour un groupe S={1;2;3;4...n} on definit la somme alternative d un sous-ensemble comme suit :
-organiser les elements par ordre decroissant
-alterner somme et soustraction es elements
exemple, le sous ensemble {3;6;9;2;7} --> 9-7+6-3+1=6
pour n=7 calculer la somme des sommes alternatives de tout les sous-ensembles de S

bonne chance

En attendant que ElIdrissi poste la réponse ... je propose l exo 3
Montrer que si4^n + 2^n +1 est premier .. n est une puissance de 3
Hard luck.

Exo 2 solution:
soit k de S_7, on calculera combien de fois ce k sera précédé d'un + et cb de fois sera-t-il précédé d'un -
les "-" : il s'agit du nombre de sous ensembles où k a une position pair.
et c'est
Pour les + , cest le nbre de sous ensembles ou k a une position impaire. et C'est:
Donc pour un k donné =/= 7, au total nous aurons :  

Il nous reste alors le cas de k=7, dans lequel  on n'aura que des + dont le nombre est de 2^6
Ce qui fait que la somme des sommes alternatives est de 7.2^6

Exercice 3: solution
on suppose que n n'est pas une puissance de 3 et on pose n=3^k .m avec m premier avec 3
On va demontrer dans ce cas que 4^n + 2^n +1 ne peut etre premier .
On pose 2^(3^k)=x alors
On montre par reccurence que
Par rapport a m=1 ou m=2 c'est Clair .

cette recurrence est mal faite, car en fait jaurais du en faire 2, une pour le cas de 3k+1 et une autre pour 3k+2.
Ainsi pour tout m premier avec 3, 4^n + 2^n +1 nest pas premier , ce qui prrouve que n doit etre une puissance de 3 .

Désolé pour la mauvaise redaction :/

Desolé pour le retard :/
Exercice 4:
trouver toutes les fonctions de R vers R tq, pour tous x,y de R²:
f(f(x)-f(y))=(x-y)².f(x+y)

f (x)=0 .. f (x)=x^2...f (x)=-x^2 Je posterai la soluc apres . Je propose donc cet exercice : Montrer que n^2 divise (n+1)^n - 1
Bonne chance.

(n+1)^n -1 =sum i=1 a i=n de C(i;n).n^i
n^2 divise clairement (n+1)^n -1 -n .C(1;n)
il suffit de preouver que n^2 | n .C(1;n) ou n|C(1;n) =n
CQFD

a fair coin is tossed 10 times, what is the probability that two heads never occur 2 times in a row

Pour lexercice 5 une autre solution:

elidrissi a écrit:

2y^4=(x-1)(x+1)
il est clair que PGCD(x-1 ; x+1) =2 ou 1
on a donc
x+1 =2^a .p^4
x-1 =2^b .q^4

La première des choses à remarquer c'est qu'il n'y a aucune relation entre ce que tu as posé et le PGCD.

elidrissi a écrit:

2=2^a .p^4 -2^b.q^4 avec p et q impaires
cas 1:
a=0 <==>b=0

Je ne vois pas pourquoi on a forcément p et q impairs, ni comment si a=0 alors b=0.
Je n'ai pas complété la lecture de la solution proposée...
Je te propose le document suivant, même s'il ne répond pas à l'exercice proposé mais il donne une méthode: http://arxiv.org/ftp/math/papers/0703/0703391.pdf.
Et je doute bien que cet exercice possède une solution unique, sauf si quelqu'un apporte une démonstration rigoureuse.

enfait si c est un resultat bien connu
si a.b=x^n avec pgcd(a;b)=1 on a forcement a et b des n-iemes puissances d un naturel
ca en decoule
p et q , dependent de notre choix. c est comme poser 192=3x2^6
en d autre terme on a : a=V2(x-1) et b=V2(x+1)
a=0 <==>2^a .p^ =1 [2] <==> 2^b .q^4 =1 [2] <==> b=0
parceque leur soustraction est paire.
sauf erreur

et il n y a qu une seule solution, je m'en suis assuré aupres de celui qui l'as posé
sur ce , bonne soiré

elidrissi a écrit:

enfait si c est un resultat bien connu
si a.b=x^n avec pgcd(a;b)=1 on a forcement a et b des n-iemes puissances d un naturel
ca en decoule
p et q , dependent de notre choix. c est comme poser 192=3x2^6
en d autre terme on a : a=V2(x-1) et b=V2(x+1)

Donc, il te reste de traiter le cas où le PGCD est égale à 2.

elidrissi a écrit:

a=0 <==>2^a .p^ =1 [2] <==> 2^b .q^4 =1 [2] <==> b=0
parceque leur soustraction est paire.

Pourquoi on ne peut pas avoir p impair et q pair?

non non parceque j ai multiplié par 2^a et 2^b ce qui donne les deux cas, le cas de PGCD=2 si a=1 et b>=2 ou b=1 et a>=2 , et le cas ou PGCD =1 quand a=b=0
mais c est clair .__. p et q dependent de notre choix
on a choisi a tel que 2^a || x-1 donc p est forcement impair
et on a chosi b tel que 2^b || x+1 donc q est forcement impair

elidrissi a écrit:

non non parceque j ai multiplié par 2^a et 2^b ce qui donne les deux cas, le cas de PGCD=2 si a=1 et b>=2  ou b=1 et a>=2 , et le cas ou PGCD =1 quand a=b=0
mais c est clair .__. p et q dependent de notre choix
on a choisi a tel que 2^a || x-1 donc p est forcement impair
et on a chosi b tel que 2^b || x+1 donc q est forcement impair

On a .
Que ce PGCD vaut 1 ou 2, on aura .
On aura aussi: .
Ces deux choses que tu as ne te donnent pas le droit que de dire que p et q ne peuvent pas être pairs tous les deux.
Tout ce que je cherche est que la solution proposée soit rigoureuse.

tout nombre relatif non nul peut etre ecrit de facon unique sous forme de produit d un nombre impaire
et d une puissance de 2
je ne vois toujours pas ou est le probleme ni pourquoi ma solution est incomplete

@nmo Rassurez vous , il existe bel et bien une solution unique... je posterai la solution juste apres + la solution de l equation fonctionnelle.

elidrissi a écrit:

tout nombre relatif non nul  peut etre ecrit de facon unique sous forme de produit d un nombre impaire
et d une puissance de 2
je ne vois toujours pas ou est le probleme ni pourquoi ma solution est incomplete

Il fallait normalement raffiner les choses:
Si on appelle a et b les valuations 2-addiques de x+1 et de x-1 respectivement, alors ils existent des entiers naturels m et n tels que: et .
Et on aura donc: .
Que ce PGCD vaut 1 ou 2, on aura .
On aura encore .
Et par un argument de parité, on déduit: 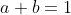, et que .
Et c'est à ce stade qu'on peut écrire 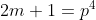et .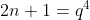
Et avec toutes ces égalités, on ne peut pas avoir l'équivalence entre a=0 et b=0 car la somme de ces entiers vaut 1.
Je te laisse vérifier ton premier cas.

ca ne sert a rien de se compliquer la vie
(x+1)(x-1)=2^(a+b).mn =2.y^4 avec m et n impaires et premiers entre eux ==> m et n sont des 4-iemes puissances d un entier

et c est justement le fait qu ils ne somment pas un 1 qui mene a une contradiction . je ne vois pas ou est le probleme
x-1=2^a .p^4
x+1 =2^b .q^4
leur difference est paire, donc si l un d x-1 et x+1 est impair l autre est impaire aussi! ce qui mene justement a la contradiction

elidrissi a écrit:

ca ne sert a rien de se compliquer la vie
(x+1)(x-1)=2^(a+b).mn =2.y^4 avec m et n impaires et premiers entre eux ==> m et n sont des 4-iemes puissances d un entier

C'est le résumé de ce que j'ai dit dans mon message d'avant, et qui n'était pas explicite dans ta solution.
Même si ta réponse n'est pas bien rédigé, j'ai bien arrivé à l'endroit où tu as commis une erreur d'inattention:

elidrissi a écrit:

1=p^4 -2q^4
une solution plus petite a l equation d origine

En effet, le 2 n'existe pas et on tombe rapidement sur p=1 et q=0.
Et cela donne bien l'unique couple solution (1,0).

ca ne sert a rien de mentionner l evident , ca decoule directement de ce qui viens avant

x^2-2y^4=1 passant par modulo 4 on a y=2b  donc (x-1)(x+1)=2^5*b^4  
Considerons deux cas  x=4a+1 ... x=4a-1
1)  x=4a+1 ==>  8a (2a+1)=2^5*b^4 ==> a=4m ==> m (8m+1)=b^4 le discriminant est egal a 1+32b^4 (imperativement un carre parfait) ==> 1+32b^4=d^2 ==> 32b^4=(d-1)(d+1)
Considerons autre fois 2 cas --
A) Si d=1(16)  b^4= (d-1)/16 (d+1)/2  comme pgcd (d+1/2 ; d-1/16)=1 on a d=16u^4+1  et d=2v^4-1  ==>8u^4=v^4-1 ==> v=2p+1 l equation se reecrit  p (p+1)(2p^2+2p+1)=u^4 comme le pgcd de ces 3 facteurs est 1 .. on a p=n^4 et p+1 =m^4  d'ou n^4+1=m^4 (impossible par Fermat-Wiles sauf pour p=0 d'ou en remontant on truve la solution (0; 1)
b) si d=-1 (16)  d=2u^4+1  et d=16v^4-1  ==> 8v^4-1=u^4 impossible mod 4 .
2) Cas ou x=4a-1  ==> 8a (2a-1)=2y^4 comme y=2b  a(2a-1)=2b^4  d''ou.  a=4m d ou   m (8m-1)=b^4  le discriminant est le mm du cas 1 ... CQFD