| | JEU D'ÉTÉ 2014 . |  |
|
+5L-W-P nmo legend-crush elidrissi bianco verde 9 participants |
|
| Auteur | Message |
|---|
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 23 Juin 2014, 14:20 Lun 23 Juin 2014, 14:20 | |
| Pour ne pas en rester là! Je propose cet exercice : (assez dur ; enfin pour moi..)
Trouver tous les nombres premiers p et q tels que 2^p +2^q est divisible par pq .
Bonne chance !
| |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 23 Juin 2014, 18:46 Lun 23 Juin 2014, 18:46 | |
| dans ce cas je poste ma solution de l exo de combi
soit An une suite de piles/ faces qui satisfait la condition et de longueur n (pas 10, n)
sot Pn l ensemble des elements de An qui finissent avec pile
soit Hn l ensemble des elements de An qui finissent avec face
|P(n+1)| = |Pn |+|Hn| parcequ en obtient un element de P(n+1) en ajoutant une pile apres un element de Pn ou Hn
|H(n+1)| = |Pn | parcequ en obtient un element de F(n+1) en ajoutant une face a un element de Pn , si on ajoute une face a un element de Fn le resultat obtenu ne serait pas permis
on a donc
| P(n+2)| = |P(n+1)|+|H(n+1)|= |P(n+1)|+|Pn|
on a
| P1|=1
|P2|=2
on obtient donc |Pn|=F(n+1) ou Fn est l nieme nombre de fibonacci
A10 =P10+H10 =P10+P9 =P11= H12 =144
la probabilitee est donc 144/2^10=9/64 | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 23 Juin 2014, 20:48 Lun 23 Juin 2014, 20:48 | |
| - bianco verde a écrit:
- Pour ne pas en rester là! Je propose cet exercice : (assez dur ; enfin pour moi..)
Trouver tous les nombres premiers p et q tels que 2^p +2^q est divisible par pq .
Bonne chance !
 on remplace dans la première équation, les diviseurs de 6 premiers sont 2 et 3 les solutions sont les couples (2,2);(2;3);(3;2) | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 23 Juin 2014, 20:51 Lun 23 Juin 2014, 20:51 | |
| Mr. LWP , p et q ne sont pas necessairement pairs , tu nas analysé quun cas ou lun des deux nombre est egal à 2
Amicalement ; | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 23 Juin 2014, 21:01 Lun 23 Juin 2014, 21:01 | |
| et comment le pq va diviser 2^p+2^q
on doit avoir au moins l'un deux pair et puisqu'ils sont premiers (p=2 ou q=2)
SAUF ERREUR | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Mar 24 Juin 2014, 00:11 Mar 24 Juin 2014, 00:11 | |
| non L-W-P , parcequ on a divise est non pas egal. un nombre impair peut diviser un nombre pair. c est le contraire qui n est pas permis | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Mar 24 Juin 2014, 00:46 Mar 24 Juin 2014, 00:46 | |
| J'avais bien signalé que le problème n'est pas si simple !!!
| |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Mar 24 Juin 2014, 18:59 Mar 24 Juin 2014, 18:59 | |
| bon voila ma solution
p=q conduit clairement a p=q=2
WLOG, p>q
comme L-W-P a deja traité le cas ou l un 2 est egal a 2, WLOG : p>q>2
pq| 2^q (1+2^(p-q) ) ==> pq| 1+2^(p-q) ==> 1+2^(p-q) =0 [p] et 1+2^(p-q)=0 [q]
comme p et q sont tout 2 impaires leur difference est divisible par 2
comme je n a pas le temps d ecrire en latex (je m en excuse) , posons Xk =2^[(p-q)/2^k ] pour tout k
X1 ^2 =-1 [p] et x^2 =-1 [q]
ce qui donne p=1 [4] et q=1 [4]
supposons que p=1 [2^k] et q=1 [2^k]
on aura donc Xk entier et :
(Xk)^(2^k) =-1 [p] ; (Xk)^(2^k) =-1 [q]
et comme
Xk ^(p-1) =1 [p] et Xk^(q-1) =1 [q]
comme p-1 =2^k.a et q-1 =2^k.b pour des entiers a et b
on aura forcement a et b pairs ce qui conduit a p=1 [2^(k+1)] et q=1[2^(k+1)]
par reccurence q-1 et p-1 acceptent une infinitee de diviseurs de la forme 2^k et sont donc nuls
ce quiconduit a p=1 et q=1 ce qui contradit le fait qu ils sont premiers
les solutions sont donc (2;2) (2;3) (3;2)
sauf erreur
Dernière édition par elidrissi le Dim 13 Juil 2014, 18:11, édité 1 fois | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Mar 24 Juin 2014, 21:43 Mar 24 Juin 2014, 21:43 | |
| je propose une autre dio
resoudre en N
x²(x² +y )=y^(m+1) | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 29 Juin 2014, 19:31 Dim 29 Juin 2014, 19:31 | |
| on pose n=x².
L'équation n²+ny-y^(m+1)=0 admet une solution entiere ssi son discriminant est un carré.ie l'existance de z tel que : y²+4y^(m+1)=z² . en particulier y divise z et on pose z=ky et donc on a 1+4y^(m-1)=k². si m=2p+1 alors on a (k-2y^p)(k+2y^p)=1 qui est facile a resoudre.
si m=2p : puisque k est impaire on pose k=2q+1 et donc on a y^(2p-1)=q(q+1) .alors q=y^s et q+1=y^r et facilement on en deduit le resultat | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 30 Juin 2014, 21:08 Lun 30 Juin 2014, 21:08 | |
| bonsoir
bon ma solution
m=0 ==>x=y=0
pour y=/=0
on multiplie par 4 et ajoutons y² partout
(2x²+y)² =4y^m+1 +y²
m=1 ==> 5y² est un carré, impossible
donc m>1 ==> y²|(2x²+y)² ==> y|2x²
posons 2x²=ay
2x²(2x²+2y)=4.y^(m+1)
(ay)(ay+2y)=4y^(m+1)
a(a+2)=4.y^(m-1)
clairement a est pair, posons a=2b
2b(2b+2)=4.y^(m-1)
b(b+1)=y^(m-1)
comme y=/=0 b=/=0
comme PGCD(b;b+1)=y^(m-1) , b et b+1 sont les m-1 iemes puissances d un entier
si m>=3 on aura une contradiction selon le theoreme de Catalan, donc m=2
sela reduit a
b(b+1)=y
2x²=ay=2b²(b+1)
x²=b²(b+1) ce qui implique b+1=k² pour un certain k de N
les solutions sont donc
x=k(k²-1)
y=k²(k²-1)
m=2
sauf erreur | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 30 Juin 2014, 21:09 Lun 30 Juin 2014, 21:09 | |
| que chacun se sente libre de poster un exo  | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Mer 02 Juil 2014, 17:30 Mer 02 Juil 2014, 17:30 | |
| Je propose jne inégalité ;
a, b, c> 0 tq a^2+b^2+c^2=a+b+c mq
(ab)^2 +(bc)^2 +(ac)^2 =< ab+bc+ac | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 | |
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 06 Juil 2014, 14:02 Dim 06 Juil 2014, 14:02 | |
| trouver les fonctions 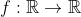 vérifiants : 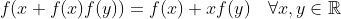 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 07 Juil 2014, 19:54 Lun 07 Juil 2014, 19:54 | |
| - elidrissi a écrit:
- bon voila ma solution
p=q conduit clairement a p=q=2
WLOG, p>q
comme L-W-P a deja traité le cas ou l un 2 est egal a 2, WLOG : p>q>2
pq| 2^q (1+2^(p-q) ) ==> pq| 1+2^(p-q) ==> 1+2^(p-q) =0 [p] et 1+2^(p-q)=0 [q]
comme p et q sont tout 2 impaires leur difference est divisible par 2
comme je n a pas le temps d ecrire en latex (je m en excuse) , posons Xk =2^[(p-1)/2^k ] pour tout k
X1 ^2 =-1 [p] et x^2 =-1 [q]
ce qui donne p=1 [4] et q=1 [4] Normalement, d'après Fermat X1 est congru à 1 modulo p et non pas à -1. Et même en acceptant cela, tu ne détaille pas comment tu passes au fait que p et q sont congru à 1 modulo 4. Même si tu penses que ces détails sont futiles, il faut au moins signaler ce que tu as fait mais donner un résultat sans justification est rien. Le début de la résolution de L-W-P me semble correcte, même si il y a une faute de frappe... La solution de l'autre exercice d'arithmétique me semble aussi correcte, et bien faite. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 13 Juil 2014, 16:31 Dim 13 Juil 2014, 16:31 | |
| p|(2^(p-q)) +1 donc forcement les Xk sont congrus a -1 modulo p et modulo q
il y a juste une erreur de frappe :Xk =2^[(p-q)/2^k ] et non p-1
et il n y as pas besoin de detailler
p|a^2+b^2 et p=3[4]==> p|a et p|b
p|a^2+b^2 et p ne divise ni a ni b ==> p=1 [4]
les lemmes de bases pour l NT ._.
ca commence bien mais le reste est faut. 2^p +2^q est pair ==> p est pair ou q est pair....? il faut une preuve . c est ce que j essaie de fournir
pour l autre exercice je n ai pas dis que c est faut, j ai juste posté une solution complete.
et merci | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 12:48 Dim 21 Sep 2014, 12:48 | |
| une autre solution : Demontrez ce qui suit : il n'existe pas d'entiers n tel que m|n^{m-1}-1 pour m impair ; et puis essayez de trouver dans notre exercice que pq|2^{pq-1}-1 .
Proposez un autre exercice en arithmétique qu'on puisse continuer !
Merci d'avance .. | |
|
  | |
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 13:07 Dim 21 Sep 2014, 13:07 | |
| Soient a et b des entiers strictement positifs vérifiant : 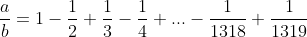 Monter que 1979 divise a bonne chance | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 13:36 Dim 21 Sep 2014, 13:36 | |
| A PEN problem ; -1/2-1/4...-1/1318=1/2+1/4+..+1/1318-2(1/2+1/4+..+1/1318) donc a/b=1+1/2+..+1/1319-(1+1/2+..+1/659)=(1/660+1/661+...+1/1319)+(1/660+1/1319)+(1/661+1/1318)+....=1979K EN DEDUIRE | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 14:03 Dim 21 Sep 2014, 14:03 | |
| a moi ;Soit m etn deux entiers naturels , montrer que si 24|mn+1 alors 24|m+n | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 15:04 Dim 21 Sep 2014, 15:04 | |
| il suffit de voir que
m+n+mn+1=(m+1)(n+1)
et m+n-mn-1=-(m-1)(n-1)
...
EXO
Montrer que les nombre de Fermat sont premiers entre eux. | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Dim 21 Sep 2014, 22:02 Dim 21 Sep 2014, 22:02 | |
| | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 22 Sep 2014, 19:58 Lun 22 Sep 2014, 19:58 | |
| EXOa,b des réels positifs non nuls avec ab>=(1/a)+(1/b)+3 prouver que  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  Lun 22 Sep 2014, 21:15 Lun 22 Sep 2014, 21:15 | |
| Il y a un exercice proposé: - bianco verde a écrit:
- a moi ;Soit m et n deux entiers naturels , montrer que si 24|mn+1 alors 24|m+n
Et une réponse qui ne me satisfait plus: - legend-crush a écrit:
- il suffit de voir que
m+n+mn+1=(m+1)(n+1)
et m+n-mn-1=-(m-1)(n-1)
... Comment ces égalités mènent-elles au résultats? - L-W-P a écrit:
- EXO
a,b des réels positifs non nuls avec ab>=(1/a)+(1/b)+3
prouver que
 Je trouve que c'est très facile: On a d'après l'inégalité arithmético-géométrique: ^{\frac{1}{3}}(\frac{1}{a^{\frac{1}{3}}}+\frac{1}{b^{\frac{1}{3}}})\ge\frac{1}{a^{\frac{1}{3}}}+\frac{1}{b^{\frac{1}{3}}}) . CQFD. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: JEU D'ÉTÉ 2014 . Sujet: Re: JEU D'ÉTÉ 2014 .  | |
| |
|
  | |
| | JEU D'ÉTÉ 2014 . |  |
|
