[quote="selfrespect"]
- samir a écrit:
- Bonsoir
Soient p et q deux nombres premiers distincts.
Montrer que : 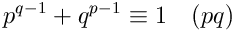
ON UTILUSE le fait que n^p=n[p] (p premier) ( qqsoit n de N)
alors on a p^q=p[q] et puisque p#q et premier ==> pgcd(p,q)=1
donc p^(q-1)=1[q]
de meme on q^(p-1)=1[p]
alors q/p^(q-1)-1 et p/q^(p-1)-1
==>pq/[p^(q-1)-1][q^(p-1)-1][/quo
[p^(q-1)-1][q^(p-1)-1]=0[pq]
p^(q-1)q^(p-1)-[p^(q-1)+q^(p-1)]+1=0[pq]

desol" Mr pco je crois que cest reglé

==>[p^(q-1)+q^(p-1)]=1[pq] (car p^(q-1)q^(p-1)=0[pq])

