| | equa-fct |  |
|
|
| Auteur | Message |
|---|
Sinchy
Expert sup

 Nombre de messages : 604 Nombre de messages : 604
Age : 37
Date d'inscription : 06/10/2006
 |  Sujet: equa-fct Sujet: equa-fct  Dim 06 Mai 2007, 10:40 Dim 06 Mai 2007, 10:40 | |
| trouver toutes les fcts qui verifies de IR-->IR et n £ IN 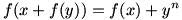 | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Lun 07 Mai 2007, 06:49 Lun 07 Mai 2007, 06:49 | |
| Bonjour Sinchy! - Sinchy a écrit:
- trouver toutes les fcts qui verifies de IR-->IR et n £ IN
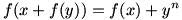 Voilà un problème qui me paraît très compliqué. C'est surtout l'absence de continuité qui est difficile. Je vais traiter partiellement le cas n=0 et totalement les autres cas. 1) n=0. L'équation est donc f(x+f(y))=f(x)+1 Je ne sais pas trouver toutes les solutions à cette équation mais il y en a avec l'axiome du choix (ce me semble). Exemple : Soit "a" un nombre irrationnel. Soit la relation d'équivalence "==" sur R : x==y <=> il existe z1 et z2 entiers relatifs tels que x-y = z1 +az2 (on vérifie aisément que c'est une relation d'équivalence). Soit A un ensemble de représentants de toutes les classes d'équivalence de "==" et s(x) la fonction qui à tout réel associe son représentant dans A (je crois que là il faut l'axiome du choix), soit h une application quelconque de A dans Z. Soient enfin z1(x) et z2(x) les fonctions de R dans Z telles que x=s(x)+z1(x)+az2(x) La fonction f(x)=a + h(s(x))+ z2(x) répond à l'équation fonctionnelle. 2) n > 0 Si f(a)=f(b), on a a^n = b^n et donc a=b ou a=-b (au cas où n pair) Alors f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0 Donc f(f(x))=x^n et donc f(x^n)=(f(x))^n Donc f(x+z^n)=f(x)+f(z^n) Donc f(x+y)=f(x)+f(y) pour tous x et y positifs ou nuls Donc f(px)=pf(x) pour x >=0 Donc f(x+pf(y))= f(x)+p^n y^n mais f(x+pf(y))=f(x)+py^n ==> n=1 Donc n=1 Donc (en reprenant le résultat ci dessus) f(x+y)=f(x)+f(y) pour tous réels x et y Si f est continue, ceci conduit à f(x)=ax et, reporté dans l'équation initiale, a=+1 ou -1 avec deux solutions continues f(x)=x et f(x)=-x Si f n'est pas continue, on tombe dans les solutions du genre : Soit {a_i} une base de R Q-ev (avec axiome du choix) Soit {e_i} un ensemble de nombres +1 ou -1 à tout réel {x_i} on associe f(x) de coordonnées {e_i x_i} f est solution de l'équation fonctionnelle -- Patrick | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 17:35 Mar 08 Mai 2007, 17:35 | |
| bonjour
quelque point du résultat
pour x=y=0 on a f(f(0))=f(0) donc f(0)=0
pour x=0 ,on a f(f(y))=y^n
posant maintnant a=f(y) donc f(a)=y^n
f(x+y)=f[x+f(a)]=f(x)+a^n=f(x)+f(y)
donc f est linéaire
reciproquement les seules solution linéaire qui satisfait le problémes sotn f(x)=x ou -x
remarque : tu dois signaler je pense que f est monotone ce qui donne que f est injenctive
........... | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 18:17 Mar 08 Mai 2007, 18:17 | |
| - otman4u a écrit:
pour x=y=0 on a f(f(0))=f(0) Sauf si n=0 - otman4u a écrit:
- pour x=y=0 on a f(f(0))=f(0) donc f(0)=0
Pourquoi f(f(0))=f(0) entraînerait-il immédiatement f(0)=0 ? - otman4u a écrit:
- ...donc f est linéaire
reciproquement les seules solution linéaire qui satisfait le problémes sotn f(x)=x ou -x Non, c'est faux. cela n'est vrai que si f est linéaire ET continue, ce qui n'est pas dans l'hypothèse. - otman4u a écrit:
- ...remarque : tu dois signaler je pense que f est monotone ce qui donne que f est injenctive ..
Non, c'est faux. Regarde mes exemples de solutions non monotones dans le post ci-dessus. -- Patrick | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 18:47 Mar 08 Mai 2007, 18:47 | |
| - pco a écrit:
- otman4u a écrit:
- pour x=y=0 on a f(f(0))=f(0) donc f(0)=0
Pourquoi f(f(0))=f(0) entraînerait-il immédiatement f(0)=0 ?
merci d'abord pour tes precieux commaitaires oui  ta raison mais f(f(0))=f(0) entraînerait immédiatement a f(0)=0 car car posant y=0 on a f(x+f(0))=f(x)+0 donc f(0) doit etr 0 sauf . biensure si f n'est pas périodique | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 18:52 Mar 08 Mai 2007, 18:52 | |
| - otman4u a écrit:
- on a f(x+f(0))=f(x)+0
donc f(0) doit être 0 sauf . bien sur, si f est périodique Et qu'est-ce qui empêche f d'être périodique ? -- Patrick | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 18:59 Mar 08 Mai 2007, 18:59 | |
| si on pose x=-f(y) ca devient f(0)=f(-f(y))+y^n et si on repose y=0 on obtient f(0)=f(-f(0))  | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mar 08 Mai 2007, 21:38 Mar 08 Mai 2007, 21:38 | |
| - codex00 a écrit:
- si on pose x=-f(y)
ca devient f(0)=f(-f(y))+y^n
et si on repose y=0
on obtient f(0)=f(-f(0))  et ? | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 16:40 Mer 09 Mai 2007, 16:40 | |
| - pco a écrit:
- otman4u a écrit:
- on a f(x+f(0))=f(x)+0
donc f(0) doit être 0 sauf . bien sur, si f est périodique
Et qu'est-ce qui empêche f d'être périodique ?
--
Patrick 1- une question a toi : f (x)c'est un" tatbi9" ou "dalla"? 2- si f(x) d'aprés toi est periodique . alors dans ce cas f(0) est son periode alors on a pour tout a de R f(a+f(0))=f(a) poson dans f(x+f(y)) x=f(0) alors d'aprés que f(a+f(0))=f(a) on a f(f(0)+f(y))=f(y) or dans l'enoncé ona f(f(0)+f(y))=f(f(0))+y^n alors on a une contradiction donc f neut peut etre peiodique .................. - pco a écrit:
- codex00 a écrit:
- si on pose x=-f(y)
ca devient f(0)=f(-f(y))+y^n
et si on repose y=0
on obtient f(0)=f(-f(0)) 
et ? on a f(0)=f(-f(0)) et f(0)=f(f(0)) donc f(0)=0 | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 16:42 Mer 09 Mai 2007, 16:42 | |
| - pco a écrit:
- Bonjour Sinchy!
2) n > 0
Si f(a)=f(b), on a a^n = b^n et donc a=b ou a=-b (au cas où n pair)
Alors f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0
--
Patrick pourquoi f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0? la reponse de cette question peut repondre a la question que tu m'a poser au dessus;) | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 19:13 Mer 09 Mai 2007, 19:13 | |
| - otman4u a écrit:
- on a f(0)=f(-f(0)) et f(0)=f(f(0))
donc f(0)=0 Mais non. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 19:17 Mer 09 Mai 2007, 19:17 | |
| - otman4u a écrit:
- pco a écrit:
- Bonjour Sinchy!
2) n > 0
Si f(a)=f(b), on a a^n = b^n et donc a=b ou a=-b (au cas où n pair)
Alors f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0
--
Patrick pourquoi f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0?
la reponse de cette question peut repondre a la question que tu m'a poser au dessus;) En première ligne, je dis que f(a)=f(b) implique a=b ou a=-b En deuxième ligne, j'ai f(x+f(0))=f(x). Donc, conformément à la première ligne (avec a=x+f(0) et b=x), on a soit x+f(0)=-f(0) (impossible), soit x+f(0)=x et donc f(0)=0. Sur ta deuxième remarque, je n'ai aucun doute sur le fait que f(0)=0 (puisque je le démontre en deux lignes). Ce que je conteste, ce sont tes démonstrations qui manquent de rigueur. -- Patrick | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 19:28 Mer 09 Mai 2007, 19:28 | |
| - pco a écrit:
- otman4u a écrit:
- pco a écrit:
- Bonjour Sinchy!
2) n > 0
Si f(a)=f(b), on a a^n = b^n et donc a=b ou a=-b (au cas où n pair)
Alors f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0
--
Patrick pourquoi f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0?
la reponse de cette question peut repondre a la question que tu m'a poser au dessus;)
En première ligne, je dis que f(a)=f(b) implique a=b ou a=-b
En deuxième ligne, j'ai f(x+f(0))=f(x). Donc, conformément à la première ligne (avec a=x+f(0) et b=x), on a soit x+f(0)=-f(0) (impossible), soit x+f(0)=x et donc f(0)=0.
Sur ta deuxième remarque, je n'ai aucun doute sur le fait que f(0)=0 (puisque je le démontre en deux lignes). Ce que je conteste, ce sont tes démonstrations qui manquent de rigueur.
--
Patrick en ce qui concerne ta qustion de ques qui empeche f d'etre periodiqu   ta pas parler ................... ""f(a)=f(b) implique a=b ou a=-b"" ca depent peut etre si f est injective mais si c'etait le cas quilque soi f donc f(f(0))=f(0) entrainent directement a f(0)=0 petite remarque : je suis en 1sm jé mém pas etudier la lecon des equation fonctionnelle c'est pour l'anné prochaine
Dernière édition par le Mer 09 Mai 2007, 20:08, édité 1 fois | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 09 Mai 2007, 19:58 Mer 09 Mai 2007, 19:58 | |
| - otman4u a écrit:
- en ce qui concerne ta qustion de ques qui empeche f d'etre periodiqu
  ta pas parler ta pas parler
...................
""f(a)=f(b) implique a=b ou a=-b"" ca depent peut etre si f est injective
mais si c'etait le cas quilque soi f donc f(f(0))=f(0) entrainent directement a f(0)=0
petite remarque : je suis en 1sm jé mém pas etudier la lecon des equation fonctionnelle c'est pour l'anné prochaine On se calme. Je ne critique personne et respecte chacun sur ce forum, quelquesoit son niveau. Toutes mes interventions le démontrent. Du moins je le pense. Si je t'ai énervé ou vexé, je le regrette et te présente mes excuses. Ceci dit, j'ai démontré dans mon premier post que f0) valait 0 en m'appuyant sur le fait que f(a)=f(b) impliquait a=b ou a=-b. Cette dernière propriété est aussi démontrée dans mon post. Pour n>0, elle est une application directe de la propriété f(x+f(y))=x+y^n. En effet, comme je le dis, f(a)=f(b) implique f(x+f(a))=f(x+f(b)) et donc a^n=b^n, d'où le résultat. Toutes mes questions sont juste destinées à pointer des faiblesses (à mes yeux) de tes démonstrations pour que tu puisses les corriger et progresser dans le domaine des équations fonctionnelles. C'est un domaine passionnant que l'on enseigne peu et je l'ai approfondi tout seul pendant quelques dizaines d'année. J'essaie alors aujourd'hui d'aider ceux qui s'y interessent. Voilà. Bon courage et bonne continuation dans ce domaine. -- Patrick | |
|
  | |
Raa23
champion de la semaine

 Nombre de messages : 179 Nombre de messages : 179
Age : 39
Date d'inscription : 02/04/2007
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Lun 14 Mai 2007, 14:10 Lun 14 Mai 2007, 14:10 | |
| | |
|
  | |
Sinchy
Expert sup

 Nombre de messages : 604 Nombre de messages : 604
Age : 37
Date d'inscription : 06/10/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Mer 16 Mai 2007, 22:05 Mer 16 Mai 2007, 22:05 | |
| salut a tout le monde , c'etait compliqué , si on ajoute la condition de la monotonie , ca sera facile , | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Jeu 17 Mai 2007, 10:29 Jeu 17 Mai 2007, 10:29 | |
| - Sinchy a écrit:
- salut a tout le monde , c'etait compliqué , si on ajoute la condition de la monotonie , ca sera facile ,
Oui, avec la monotonie, cela devient plus simple. 1) n=0 : f(x+f(y)) = f(x)+1. f(x+f(y))=f(x+f(z)) x=1 et z=1+f(1) ==> f(x+f(1))=f(x+f(1+f(1)))=f(x+1+f(1))=f(x)+1=f(x+f(1)) ==> f(u+1)=f(u) pour tout u ==> f(u+n)=f(u) pour tous u et n Mais alors, f monotone ==> f(u)=f(u+v) pour tout u et tout v de [0,n], pour tout n Donc f est constante, ce que l'équation initiale empêche. 2) n > 0 Si f(a)=f(b), on a a^n = b^n et donc a=b ou a=-b (au cas où n pair) Alors f(x+f(0))=f(x)==> x+f(0)=x ou x+f(0)=-x ==> f(0)=0 Donc f(f(x))=x^n et donc f(x^n)=(f(x))^n Donc f(x+z^n)=f(x)+f(z^n) Donc f(x+y)=f(x)+f(y) pour tous x et y positifs ou nuls Cette équation connue (Cauchy) conduit, grace à la monotonie de f, à f(x)=cx. En remplaçant dans l'équation initiale, on a n=1 et c=+1 ou -1 Solutions donc : n=0 et pas de solution n=1 et f(x)=x ou f(x)=-x n>1 et pas de solution -- Patrick | |
|
  | |
Sinchy
Expert sup

 Nombre de messages : 604 Nombre de messages : 604
Age : 37
Date d'inscription : 06/10/2006
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  Jeu 17 Mai 2007, 12:58 Jeu 17 Mai 2007, 12:58 | |
| on a f est injective (car f est montone ) pour y=0 on a f(0)=0
et pour x=0 on a f(f(y))=y^n donc n est impair. Par conséquent f est impair et additive donc f(x)=a*x | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: equa-fct Sujet: Re: equa-fct  | |
| |
|
  | |
| | equa-fct |  |
|
