| | problème N°85 de la semaine (11/06/2007-17/06/2007) |  |
|
+17Kendor badr Yalcin aissa Jamel Ghanouchi Conan khamaths Weierstrass radouane_BNE math_pro wiles Raa23 selfrespect Bison_Fûté schwartz abdelbaki.attioui samir 21 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 12:39 Mar 12 Juin 2007, 12:39 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 12:42 Mar 12 Juin 2007, 12:42 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 14:49 Mar 12 Juin 2007, 14:49 | |
| Bonjour
Solution postée
voici la solution d'abdelbaki.attioui
Voici la solution du Pb 85
Bonjour,
2S=(somme de i=0 à n) 1/(1+x_i^k)+1/(1+x_(n-i)^k)
=(somme de i=0 à n)1/(1+x_i^k)+x_i^k/(1+x_i^k)=n+1 ==> S=(n+1)/2
A+ | |
|
  | |
schwartz
Maître
Nombre de messages : 78
Date d'inscription : 28/12/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 15:12 Mar 12 Juin 2007, 15:12 | |
| solution postée
voici la solution de schwartz
si on inverse l'ordre de la somme, et on l'ajoute a la somme initiale
on obtient n,
donc la somme vaut n/2 | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 15:30 Mar 12 Juin 2007, 15:30 | |
| Bonjour Mr SAMIR!
Solution postée
voici la solution de BOURBAKI
Bonjour Mr SAMIR.
Voici ma proposition de solution pour le problème de la Semaine Numéro 85.
Supposons n IMPAIRE n=2p+1 alors dans la somme S , on peut apparier le facteur correspondant à i et celui correspondant à n-i , il y aura en tout p+1 Paquets , chaque Paquet vaut [1/(1+xi^k)]+[1/(1+xn-i^k]= [1/(1+xi^k)]+[1/(1+(1/xi)^k]=(1+xi^k)/(1+xi^k)=1
et de là la somme S vaudra p+1=(n+1)/2
Supposons maintenant n PAIR n=2p alors dans la somme S , on fait comme précédemment , seulement dans ce cas il y aura un facteur ORPHELIN , c’est le terme d’indice p=n/2 et la somme S vaudra donc 1/(1+xp^k)+(n/2)
Sachant que xp^2=1 ( ce qui exige xp=1 )
Alors : S=1/2 +(n/2)=(n+1)/2
En conclusion et indépendemment de la parité de n , S est égale à (n+1)/2 .
Ce qui termine la solution.
AMITIES . LHASSANE ( BOURBAKI )
| |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 18:32 Mar 12 Juin 2007, 18:32 | |
| Solution postée
voici la solution de selfersept
Salut Mr Samir
on a q q soit i de {0,1...,n} xi=1/x_(n-i)=x'i
*si n est pair
alors
S=\sum _{0}^{n} 1/(1+xi^k)=[\sum_{0}^{n/2}(1/(1+xi^k)+1/]+1/2 ?
(1+x'i^k))=\sum_{0}^{n/2} (1)=n/2+1
alors S=(n+1)/2
*si n est impair de meme on trouve
S=n/2
? car n est pair alors {x_(n/2)}²=1 ==> 1/(1+1^k)=1/2 | |
|
  | |
Raa23
champion de la semaine

 Nombre de messages : 179 Nombre de messages : 179
Age : 39
Date d'inscription : 02/04/2007
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 19:37 Mar 12 Juin 2007, 19:37 | |
| Solution postée
voici la solution de Raa23
1/(1+Xi^k) = Xn-i^k/(1+Xn-i^k)
donc 1/(1+Xi^k) + 1/(1+Xn-i^k) = 1
donc 2S=n+1
S=(n+1)/2 | |
|
  | |
wiles
Expert sup

Nombre de messages : 501
Age : 34
Localisation : khouribga
Date d'inscription : 03/04/2007
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mar 12 Juin 2007, 20:43 Mar 12 Juin 2007, 20:43 | |
| solution postee
voici la solution de wiles
on sait que 1/(1+xi) + 1/(1+x(n-i))=1/(1+xi)+xi/(1+xi)=1
si n=2p+1 alors S=p+1
si n=2p alors S=p+1/(1+xp)
et on a xp*x(n-p)=xp*xp=1
si xp= - 1 c'est absurde
si xp=1 alors S=p+1/2 | |
|
  | |
math_pro
Habitué
Nombre de messages : 20
Date d'inscription : 03/12/2006
 |  Sujet: postée la solution ... Sujet: postée la solution ...  Mer 13 Juin 2007, 00:24 Mer 13 Juin 2007, 00:24 | |
| Solution postée
A BIENTOT
voici la solution de math_pro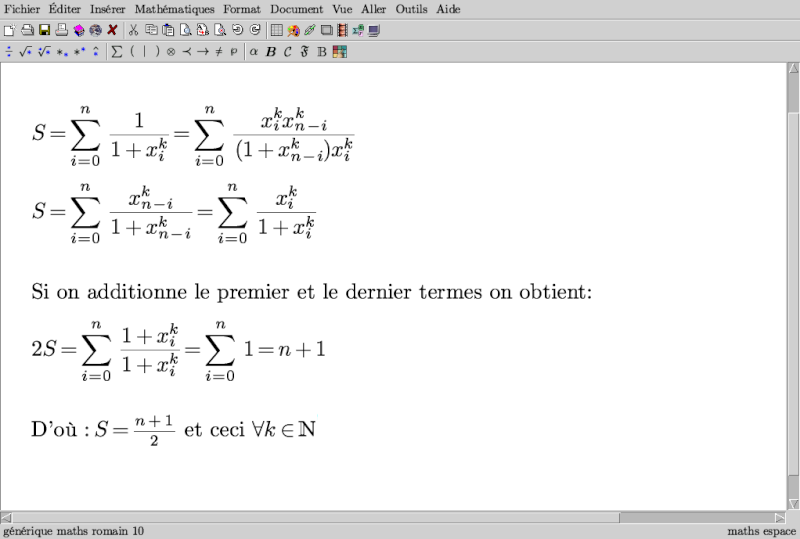 | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 09:47 Mer 13 Juin 2007, 09:47 | |
| السلام عليكم ورحمة الله تعالى وبركاته
solution postée
voici la solution de boukharfane radouane
salut tout le monde.
On a S=sigma (i=0 à i=n) (1/ (1+Xi^k) =sigma (i=0 à i=n) (Xi^k/ (1+Xi^k)
Donc 2S=sigma (i=0 à i=n) ((1/ (1+Xi^k) + (Xi^k/ (1+Xi^k))
=sigma (i=0 à i=n) de 1=n+1
D’où S= (n+1)/2 | |
|
  | |
Weierstrass
Expert sup

 Nombre de messages : 2079 Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 10:01 Mer 13 Juin 2007, 10:01 | |
| Solution postée
désolé (solution non trouvée )(administration ) | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 10:40 Mer 13 Juin 2007, 10:40 | |
| Bonjour
Solution postée
voici la solution de khamaths
Bonjour Samir
Sn = Sum_i=0^n [1/(1+xi^k)]
= Sum_i=0^n [1 - x_i/(1+xi^k)]
= (n+1 ) - Sum_i=0^n [ 1/ ( 1+ x_{n-i}^k)]
= (n+1) - Sum _i=0^n [1/( 1+ x_i^k)]
= (n+1) - Sn
====> Sn = (n+1)/2 | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 11:53 Mer 13 Juin 2007, 11:53 | |
| bnjour Mr Samir
solution posté
cordinalement
voici Solution de Conan au probleme de la semaine : N°85
on a : x_i * x_n-i = 1 <=> 1/(1+(x_i)^k) = (x_n-i)^k / (1+(x_n-i)^k)
Donc : S = sum_{i=0,n}1/(1+(x_i)^k) = sum_{i=0,n}(x_n-i)^k / (1+(x_n-i)^k)
2S =sum_{i=0,n}1/(1+(x_i)^k) + sum_{i=0,n}(x_n-i)^k / (1+(x_n-i)^k) =...= n+1
S = (n+1)/2 | |
|
  | |
Jamel Ghanouchi
Débutant
 Nombre de messages : 9 Nombre de messages : 9
Date d'inscription : 26/03/2007
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 13:11 Mer 13 Juin 2007, 13:11 | |
| Bonjour, Solution postée ! cordialement voici la solution de jamel 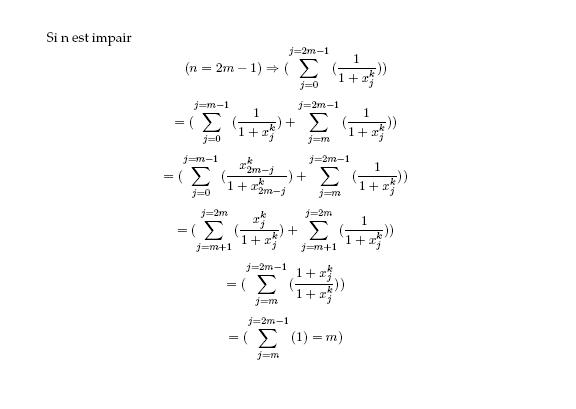 | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 15:54 Mer 13 Juin 2007, 15:54 | |
| Salut tout le monde
solution postée
voici la solution d'aissa
on a 1/(1+x^k_i)+ 1/(1+x^k_(n-i)=1
alors 2S = n+1 et S = (n+1)/2 | |
|
  | |
Yalcin
champion de la semaine
Nombre de messages : 21
Date d'inscription : 19/09/2005
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Mer 13 Juin 2007, 16:53 Mer 13 Juin 2007, 16:53 | |
| solution postée
voici la solution de yalcin
Pour tout n de IN*, Pour tout i de [0,n] ,Pour tout k de IN
on a : 1/(1+(x_i)^k)+1/(1+(x_(n-i))^k)=1
1)
Supposons n pair ,alors n=2m
D'où S(k,n)=1/(1+(x_m)^k)+Somme(1/(1+(x_i)^k)+1/(1+(x_(n-i))^k),i=0..(m-1))
Or 1/(1+(x_i)^k)+1/(1+(x_(n-i))^k)=1
D'où S(k,n)=m+1/(1+(x_m)^k)
2) Supposons n impair, alors n=2m+1
D'où S(k,n)=Somme(1/(1+(x_i)^k)+1/(1+(x_(n-i))^k),i=0..m)
D'où S(k,n)=m+1
Finalement on obtient :
En posant f(n)=(1-(-1)^n)/2 (n pair f(n)=0 ,n impair f(n)=1) , qui est utile ,car E(n/2)=(n-f(n))/2
Pour tout n de IN*,Pour tout k de IN :
S(k,n)=[(n-f(n))/2]+f(n)+[f(n+1)]*[1/(1+(x_((n-f(n))/2))^k)] | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Jeu 14 Juin 2007, 10:27 Jeu 14 Juin 2007, 10:27 | |
| solution postee
voici la solution de badr
S=sum(i=0)^{n}1/(1+x_i^(k)) telque k£N et i£{0:1:2:...:n}
S=1/(1+x_0^(k))+1/(1+x_1^(k))+...................+1/(1+x_n^(k))
alors S est une suite arthimitrique
S=(n+1)/2*(1/(1+x_0^(k))+1/(1+x_n^(k)))
S=(n+1)/2*{(1+1+x_0^(k)+x_n^(k))/(1+x_0^(k)+x_0^(k)*x_n^(k)+x_n^(k))}
alors on a x_0^(k)*x_n^(k)=1^(k)=1 (i=0 )
S=(n+1)/2*{(2+x_0^(k)+x_n^(k))/(2+x_0^(k)+x_n^(k))}
S=(n+1)/2 | |
|
  | |
Kendor
Féru
Nombre de messages : 64
Localisation : Malakoff (92240)
Date d'inscription : 13/12/2005
 |  Sujet: Solution au problème de la semaine n°85 par Kendor Sujet: Solution au problème de la semaine n°85 par Kendor  Jeu 14 Juin 2007, 10:59 Jeu 14 Juin 2007, 10:59 | |
| Bonjour!
Solution postée.
voici la solution de Kendor
On remarque que pour tout entier naturel k,1/(1+x_i^k)+1/(1+x_(n-i)^k)=1
Si n est impair :n=2p+1
Donc Sk est la somme des 1/(1+x_i^k),i variant de 0 à 2p+1
Donc Sk=somme des 1/(1+x_i^k),i variant de 0 à p + somme des 1/(1+x_i^k),i variant de p+1 à 2p+1
Si j=2p+1-i,alors Sk= somme des 1/(1+x_i^k),i variant de 0 à p + somme des 1/(1+x_(n-j)^k),j variant de 0 à p
Donc Sk= somme des 1,i variant de 0 à p
Donc Sk=p+1=(n+1)/2
Si n est pair,n=2p
Donc Sk est la somme des 1/(1+x_i^k),i variant de 0 à 2p
Donc Sk est la somme des 1/(1+x_i^k),i variant de 0 à p-1+1/(1+x_p^k)+ somme des 1/(1+x_i^k),i variant de p+1 à 2p
On applique la même méthode qu’au-dessus
Donc Sk=somme des 1,i variant de 0 à p-1+1/(1+x_p^k)
=p+1/(1+x_p^k)
Or x_p*x_(n-p)=1
Donc x_p^2=1
Donc x_p=1 car x_p>=0.
Ainsi Sk=p+1/2=(n+1)/2.
Donc dans tous les cas,Sk=(n+1)/2.
Kendor
Ciao!
A+
Kendor. | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Jeu 14 Juin 2007, 18:48 Jeu 14 Juin 2007, 18:48 | |
| Salut,  Solution postée voici la solution de codex Merci a+ | |
|
  | |
coucou
Maître

 Nombre de messages : 180 Nombre de messages : 180
Age : 34
Date d'inscription : 08/04/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Ven 15 Juin 2007, 10:51 Ven 15 Juin 2007, 10:51 | |
| Salut : Solution postée voici la solution de coucou | |
|
  | |
toetoe
Maître

Nombre de messages : 86
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Sam 16 Juin 2007, 13:10 Sam 16 Juin 2007, 13:10 | |
| bonjour,
solution postée
voici la solution de toetoe
Bonjour,
Voila ma solution :
On pose : y = x(i)^k, z=x(n-i)^k ,A(i) = (1/(1+y))+(1/(1+z)) avec yz = 1
On pose aussi : u = x(n/2)
On a : A(i) = (1/(1+y)) + (1/(yz + z)
= (1/(1+y)) ((1+z)/z)
= (1+z)/(z(1+y))
=(yz+z)/(z(1+y)
A(i) =1
- n est impaire => S = A(0) +A(1) + …….+ A((n-1)/2 )
S =((n+1)/ 2 ) * 1
S =(n+1)/2 .
- n est paire => S = A(0) + A(1) + …. +A((n-2)/2) + (1/(1+u))
On a u^2 = 1 => u = 1
Donc , est paire => S = [((n-2)/2)+1] + (1/2)
= (n+1)/2
Ainsi ,on a S = (n+1)/2
ToeToe , | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  Dim 17 Juin 2007, 11:46 Dim 17 Juin 2007, 11:46 | |
| Solution postéevoici la solution de bestfriend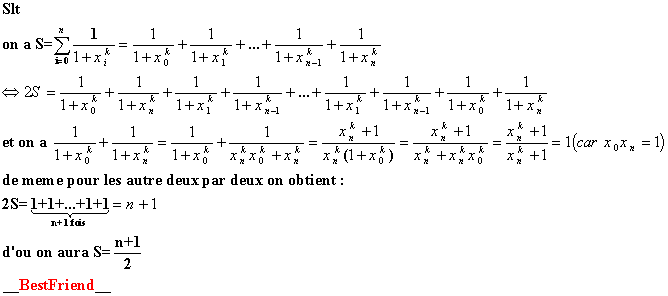 Merci __BestFriend__[/ | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007) Sujet: Re: problème N°85 de la semaine (11/06/2007-17/06/2007)  | |
| |
|
  | |
| | problème N°85 de la semaine (11/06/2007-17/06/2007) |  |
|
