problème N°98 de la semaine (10/09/2007-16/09/2007)

salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci

postée
voici la solution de abdelilah
La solution est a+b=0.

En effet:

on a (a+sqrt(a^2 +1))(b+sqrt(b^2 +1))=1 donne
a+sqrt(a^2 +1)=-b+sqrt(b^2 +1)

cad a+b=sqrt(b^2 +1) -sqrt(a^2 +1) (*)

d ou (a+b)[(sqrt(b^2 +1)+sqrt(a^2 +1))-(b-a)]=0 (**)

Si a+b n est pas 0 alors (*) et (**) donnent b=sqrt(b^2 +1) ou 1=0 , absurde.

en fin a+b=0


Abdelilah
a+

solution postée
voici la solution de conan
on a :

(a+rac(a²+1)) (b+rac(b²+1)) = 1

<=> (a-rac(a²+1)) * (a+rac(a²+1)) (b+rac(b²+1)) = (a-rac(a²+1))

<=> -b-rac(b²+1) = (a-rac(a²+1))

<=> a+b = rac(a²+1) - rac(b²+1) *

de la meme façon , on a :

(b-rac(b²+1)) * (a+rac(a²+1)) (b+rac(b²+1)) = (b-rac(b²+1))

<=> a+b = rac(b²+1)-rac(a²+1) **

de (*)et(**) on trouve que : rac(a²+1) = rac(b²+1)

donc : S = a+b = 0


a+

solution postee
voici la solution de wiles
bonjour
on a (rac(a^2+1)+a)(rac(b^2+1)+b)=1
donc rac(a^2+1)+a=rac(b^2+1)-b et rac(b^2+1)+b=rac(a^2+1)-a
en sommant les deux equations on conclut que:
a+b=0

slt tt le monde
solution postée
voici la solution de mni
slt samir
on a
(a+rac(a*2+1))(b+rac(b*2+1))=1
a+rac(a*2+1)=1/(b+rac(b*2+1))
a+rac(a*2+1)=rac(b*2+1)-b

S=rac(b*2+1)-rac(a*2+1)

salut,
solution postée.
solution non trouver (car l'email que tu m'as envoyé ne contient pas de piece jointe ) (administration )

solution postée
voici la solution de neutrino

solution postée par mp et email
merci
voici la solution de mohamed_01_01
salut : (jidr[2](x):le racine carrée de x)

on a (a+jidr[2](a²+1))(b+jidr[2](b²+1))=1

et puisque (a+jidr[2](a²+1)(-a+jidr[2](a²+1)=1 donc on va déduit que

-a+jidr[2](a²+1)=b+jidr[2](b²+1)

si -a>0 et b<0 on va deduit que -a+jidr[2](a²+1)>1 et

b+jidr[2](b²+1)<1 donc cela n'existe pas

si -a<0 et b >0 donc -a+jidr[2](a²+1)<1 et b+jidr[2](b²+1)>1

donc cela nexite pas ( -a et b on la meme signe)

-si a=0 et b=0 cela va etre juste donc a+b=0

-si -a>b>0

(puisque -a et b positive donc a²>b² donc jidr[2](a²+1)>jidr[2](b²+1) )

donc on va touver que

-a+jidr[2](a²+1)>b+jidr[2](b²+1)

et quand b>-a>0 (avec la mme methode) on va trouver que

-a+jidr[2](a²+1)<b+jidr[2](b²+1) donc si a>0 et b>0 alors b=-a donc b+a=0

-si 0>-a>b donc 0<a<-b donc

0<a+jidr[2](a²+1)<-b+jidr[2](b²+1) (il sont positive car que soit x jidr[2](x²+1)>(x et -x)) donc on va déduit que

1/(a+jidr[2](a²+1))>1/(-b+jidr[2](b²+1))

1/(a+jidr[2](a²+1))=-a+jidr[2](a²+1)

1/(-b+jidr[2](b²+1))=b+jidr[2](b²+1) donc

-a+jidr[2](a²+1)>b+jidr[2](b²+1)

et avec la meme methode pour 0>b>-a on va déduit que

-a+jidr[2](a²+1)<b+jidr[2](b²+1) donc b=-a alors a+b=0

donc dans tout les etats on a trouver que S=a+b=0

solution postée
voici la solution de huntersol

salut
solution postée !

voici la solution de einshtein!

deux methodes:
voici 1:

et 2: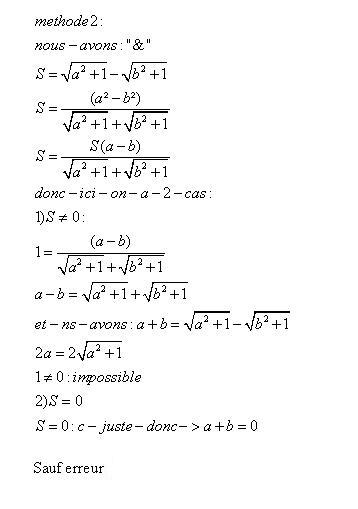


a+

solution postée
voici la solution de badr_210
bonsoir Samir
voici la solution de badr_210
nous remarquons clairement que le couple (0,0) résou l'équation donc S=a+b=0 , mais celà n'es pa suffisant il faut montrer ke c le seul
on a : (a+V(a²+1))(b+V(b²+1))=1
et
[(a+V(a²+1))+(b+V(b²+1))]²=(a+V(a²+1))²+(b+(b²+1))²+2
et ce là implique ke (a+V(a²+1))=1 et (b+V(b²+1))=1
<=>a=0 et b= 0
d'ou S=a+b =0

solution poster
voici la solution de ali20/20
remarque que
(v(a^2+1)+a)(v(a^2+1)-a)=1
(v(b^2+1)+b)(v(b^2+1)-b)=1
et on a
(v(a^2+1)+a)(v(b^2+1)+b)=1 donc
(v(a^2+1)-a)(v(b^2+1)-b)=1
posant v(a^2+1)=x v(b^2+1)=y (pour faciler l'ecriture )

alors (x+a)(x+b)=1 et (x-a)(x-b)=1
on conclut que
ay+bx=0
donc
b(v(a^2+1))+a(v(b^3+1))=0
alors
b^2(a^2+1)=a^2(b^2+1)
donc a^2-b^2=0
alors
(a-b)(a+b)=0
suposant que a-b=0
alors a=b alors (v(a^2+1)+a)^2=1 alors ce cas est impossible
alors il reste que (a+b=0)
en verifions la reponse
doncs=0
v = racine (je pense que la solution est juste )
merci d'avance samir
ali20/20

postée
voici la solution de mahdi
Soit a et b deux reels tel que : *
On multiplie le premier membre de l'equation par
On obtient **
* <==>
** <==>
la difference des deux equations precedantes donne :

donc
d'ou a-b=0 ou a+b=0

Si a=b alors
donc a+b=0
S=0

solution postee
solution non trouver (administration )

salut et merci
solution postée
voici la solution de otman4u
salut
on pose a+V(a²+1)=x et b+V(b²+1)=1/x
oon met le caré et on aurra
2a²+1+2aV(a²+1)=x² et 2b²+1+2bV(b²+1)=1/x²
2a(a+V(a²+1) )+1-x²=0 et 2b(b+V(b²+1) )+ 1 -1/x²=0
2ax+1-x²=0 et (2b)/x +1 -1/x²=0
a=(x²-1)/2x et b=(1/x²-1)/(2/x) = [(1-x²)x²]/(2x/x²)=(1-x²)/2x
donc a=-b d'ou S=a+b=0
otman4u

postée
voici la solution de coucou
d'après le terme qu'on a , on aura : -(b+rac(b²+1))=a-rac(a²+1)
ça donnera a+b=rac(a²+1) - rac (b²+)1
de meme on aura a+b=rac (b²+1) - rac (a²+1)
ce qui donne en sommant : a+b=0

Bonjour!

Solution postée.
voici la solution de kendor
Soit f(x)=x+√(x²+1)
f’(x)=1+x/√(x²+1)= (√(x²+1) +x)/√(x²+1)=f(x)/√(x²+1)
x²+1>x²
Donc √(x²+1)>√(x²)=|x|>=-x
Donc f(x)=√(x²+1) +x>0
Donc f’(x)>0
Donc f est strictement croissante de IR dans] 0, +∞ [
Donc f est injective.

Pour x réel, soit E(x)= {y réels tels que f(x)f(y)=1}
E(x)≠ Ø car –x est dans E(x).
En effet f(x)f (-x)=[x+√(x²+1)] [-x+√ ((-x)²+1)]=x²+1-x²=1

Soient maintenant x et y réels tels que f(x)f(y)=1
Alors par définition y est dans E(x)
Soit y’ dans E(x)
Alors f(x)f(y)=1=f(x)f (y’)
f(x) étant non nul, on a f(y)=f (y’)
Ce qui entraîne y=y’ car f est injective.

Donc E(x) est un singleton.
Donc E(x)= {-x}
Donc x+y=0.

Ciao!
A+

Kendor

salut samir
solution postée
Voici la solution jimmy
[a+rac(a^2+1)][b+rac(b^2+1)]=1
Pour a: a=1/[b+rac(b^2+1)] – rac(a^2+1)
Pour b : b=1/[a+rac(a^2+1)] – rac(b^2+1)
S=a+b
=1/[b+rac(b^2+1)] – rac(a^2+1) + 1/[a+rac(a^2+1)] – rac(b^2+1)
=1/[b+rac(b^2+1)] – rac(b^2+1) + 1/[a+rac(a^2+1)] – rac(a^2+1)
=[1-a*rac(a^2+1) - a^2 – 1] / [a+rac(a^2+1)] + [1-b*rac(b^2+1) - b^2 – 1] / [b+rac(b^2+1)]
= - (a+b)
Puisque : a+b = - (a+b)
Alors : a+b = 0
Donc S = 0

@+

Rebonjour tout le monde , et ramadan mobarek saiid ,
solution postée ,
a bientot.
(1313)
voici la solution de selfrespect
Salut Mr Samir ,et ramadan mobarek saiid.
♦l'identité multipliée par (rac(b²+1)-b) ==> a+rac(a²+1)=rac(b²+1)-b
==> a+b=rac(b²+1)-rac(a²+1)
de mm on trouve( multipliée par (rac(a²+1)-a) :
a+b=rac(a²+1)-rac(b²+1)=-(a+b)
donc a+b=0.
a+

solution postée
voici la solution de 3afrit
c'est ma premiere participation :
S = racine (2ab-1)
ou bien
S = - racine (2ab-1)
ou bien
S = 2b
ou bien
S = 2a

Salut tout le monde ! Ramadan moubarak !!

Solution postée
voici la solution de m&m
[a+V(a^2+1)] [b+V(b^2+1)] = 1 {V=racine de}



a+V(a^2+1) = 1 / b+V(b^2+1)



a = [1 / b+V(b^2+1)] - V(a^2+1)



b+V(b^2+1) = 1 / a+V(a^2+1)



b = [1 / a+V(a^2+1)] - V(b^2+1)



S = [1 / b + V(b^2+1)] + [1 / a + V(a^2+1)] - V(b^2+1) - V(a^2+1)



S = [ a + V(a^2+1) + b + V(b^2+1) ] / [[a+V(a^2+1)] [b+V(b^2+1)]] - V(b^2+1) - V(a^2+1)



S = a + V(a^2+1) + b + V(b^2+1) - V(b^2+1) - V(a^2+1)



S = a+b