| | problème N°123 de la semaine (03/03/2008-09/03/2008) |  |
|
+6Kendor abdou20/20 amine-b iverson_h3 memath samir 10 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: problème N°123 de la semaine (03/03/2008-09/03/2008)  Lun 03 Mar 2008, 18:30 Lun 03 Mar 2008, 18:30 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Lun 03 Mar 2008, 18:33 Lun 03 Mar 2008, 18:33 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
Invité
Invité
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Lun 03 Mar 2008, 19:12 Lun 03 Mar 2008, 19:12 | |
| Solution postée  solution non trouver solution non trouver |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Lun 03 Mar 2008, 21:06 Lun 03 Mar 2008, 21:06 | |
| solution postee voici la solution de memath | |
|
  | |
iverson_h3
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 08/09/2007
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Mar 04 Mar 2008, 19:17 Mar 04 Mar 2008, 19:17 | |
| solution postée  | |
|
  | |
amine-b
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 34
Date d'inscription : 12/11/2007
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Mar 04 Mar 2008, 19:37 Mar 04 Mar 2008, 19:37 | |
| solution postée !!!!! 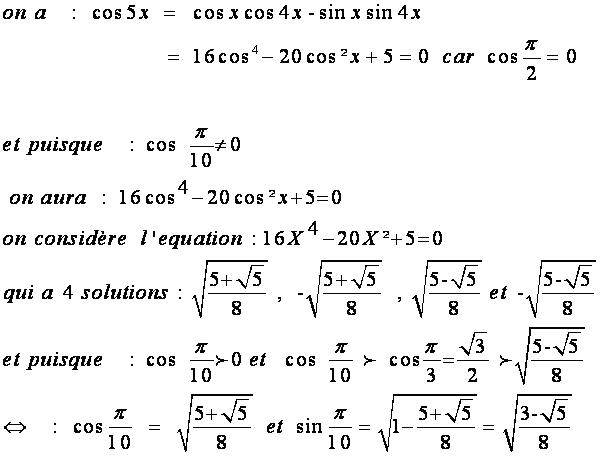 | |
|
  | |
abdou20/20
Expert sup

 Nombre de messages : 713 Nombre de messages : 713
Age : 33
Localisation : rabat
Date d'inscription : 12/06/2007
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Mar 04 Mar 2008, 21:24 Mar 04 Mar 2008, 21:24 | |
| solution posteeee on montre que cos(5a)=16cos^5a-20cos^3a+5cosa consideron la fonction f(x)=16x^5-20x^3+5x+1=(x+1)(4x²-2x+1)² f s annulle lorsque x=-1 x=(1+racine(5))/4 x=(1-racine(5))/4 alors cos PI /5=(1+racine(5))/4 on va utiliser la formule de trigo. cos(2A) = 2 (cosA)² - 1 en prenant A=  On obtient ainsi  = 2 (cos (\frac{\pi}{10}))^2 - 1) C'est à dire  = 2 (cos (\frac{\pi}{10}))^2 - 1) Donc )^2=\frac{1+cos(\frac{\pi}{5})}{2}) Donc =\sqr{\frac{1+cos(\frac{\pi}{5})}{2}}) puis on va deduir le resultat =\L{\sqr{\frac{1+\frac{1+\sqr5}{4}}{2}}=\sqr{\frac{5+\sqr5}{8}}}) | |
|
  | |
Kendor
Féru
Nombre de messages : 64
Localisation : Malakoff (92240)
Date d'inscription : 13/12/2005
 |  Sujet: Solution au problème de la semaine n°123 par Kendor Sujet: Solution au problème de la semaine n°123 par Kendor  Mer 05 Mar 2008, 10:30 Mer 05 Mar 2008, 10:30 | |
| Bonjour!
Solution postée.
voici la solution de kendor
Soit x=sin (π/10) et y=cos (π/10)
π/10=π/2-2π/5
Donc x=cos (2π/5) et y=sin (2π/5)
Soit z=x+iy
Alors z^5=1
Donc 1+z+z²+z³+z^4=0
Donc 1+2cos (2π/5) +2cos (4π/5)=0
Donc 1+2x+2(2x²-1)=0
Donc 4x²+2x-1=0
∆=20
Donc x= (-2+√20)/8= (√5-1)/4
y=√ (1-x²)
=√ (1-(6-2√5)/16)
=√ ((10+2√5)/16)
=√ (10+2√5)/4.
Donc x=sin (π/10)= (√5-1)/4
Et y=cos (π/10)=√ (10+2√5)/4.
Ciao!A+
Kendor | |
|
  | |
abdelilah
Maître

 Nombre de messages : 206 Nombre de messages : 206
Localisation : Lblad
Date d'inscription : 22/08/2006
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Mer 05 Mar 2008, 19:57 Mer 05 Mar 2008, 19:57 | |
| Bonjour,
solution postee .
voici la solution d'abdeilah
On a cos(5x)=16*cos(x)^5-20*cos(x)^3+5*cos(x)
par resolution de
16*x^5-20*x^3+5*x = x*(16*x^4-20*x^2+5)
dont les solutions sont
0, -1/4*\sqrt(10+2*\sqrt{5}), 1/4*\sqrt(10+2*\sqrt{5}),
-1/4*\sqrt(10-2*\sqrt{5}), 1/4*\sqrt(10-2*\sqrt{5})
et puisque cos(5x)=0
<===> x=\pm \frac{\pi}{10}+\frac{2k \pi}{5} (\pm veut dire + ou - )
par ordres de ces solutions on a cos(\frac{\pi}{10}) est la plus grande des solutions donc = a 1/4*\sqrt(10+2*\sqrt{5})
et par sin(\frac{\pi}{10})>0 et sin^2 +cos^2 x = 1 on trouve
sin(\frac{\pi}{10})=1/2*\sqrt(4-\sqrt(10+2*\sqrt{5}))
Remarque: on pourra se poser la question: construire un angle dont la mesure est \frac{\pi}{10}.
Abdelilah
a+ | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Mer 05 Mar 2008, 22:25 Mer 05 Mar 2008, 22:25 | |
| Bonsoir
Solution postée
voici la solution de khamaths
Bonjour Samir
On a :**sin(4pi/10)= cos(pi/10)
d'autre part **sin(4pi/10)=2sin(2pi/10)cos(2pi/10) = 4 sin(pi/10)cos(pi/10)cos(2pi/10)
======>4sin(pi/10)cos(2pi/10) = 1
======>4sin(pi/10)[1-2sin²(pi/10)] =1 (E)
Posons: t= sin(pi/10) > 0
(E) <===>8t^3-4t+1=0
<====>(t-1/2)(8t²+4t-2)=0
<======>4t² +2t-1 =0 (t # 1/2)
<=====>sin(pi/10) = t = (-1+rac5)/4
=====>cos(pi/10) = rac(10+2rac5)/4 (cos (pi/10) > 0 ) | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Jeu 06 Mar 2008, 19:25 Jeu 06 Mar 2008, 19:25 | |
| salotion postée
solution non trouver | |
|
  | |
L
Expert sup

 Nombre de messages : 1558 Nombre de messages : 1558
Age : 33
Date d'inscription : 03/09/2007
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  Jeu 06 Mar 2008, 20:36 Jeu 06 Mar 2008, 20:36 | |
| solution postée
voici la solution de L
tout dabord on calcule cos pi/10
on calcule cos 5 pi/10=cospi/2=0
dautre part on sait que cos5x=cosx(16cos^4x-20cos²x+5)
on applique ona alors cospi/10=0ou 16cos^4pi/10-20cos²pi/10+5=0 la premiere impossible on pose X=cos²pi/10 et on resoud l'equation
X=20-rac80/32 impossible car X>0 donc cospi/10=rac(20+rac80/32)
dautre part sinpi/10=rac(1-rac(20+rac80/32))
j'espere que c'est correct | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008) Sujet: Re: problème N°123 de la semaine (03/03/2008-09/03/2008)  | |
| |
|
  | |
| | problème N°123 de la semaine (03/03/2008-09/03/2008) |  |
|
