| | problème N°144 (28/07/2008-03/08/2008) |  |
|
+10joystar1 ilham_maths mohamed_01_01 Conan badr_210 y-a-ss-i-n-e abdellatif radouane_BNE rachid18 samir 14 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°144 (28/07/2008-03/08/2008) Sujet: problème N°144 (28/07/2008-03/08/2008)  Lun 28 Juil 2008, 16:48 Lun 28 Juil 2008, 16:48 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Lun 28 Juil 2008, 16:50 Lun 28 Juil 2008, 16:50 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
rachid18
Expert grade2

 Nombre de messages : 369 Nombre de messages : 369
Age : 32
Date d'inscription : 23/03/2008
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Lun 28 Juil 2008, 18:00 Lun 28 Juil 2008, 18:00 | |
| Solution postée.
L'inégalité est équivalente à:
(a+2b)²+2c² >= 96
Or par AM-GM on a:
(a+2b)²+2c² >= 8ab+2c² >= 128/c +128/c +2c² >= 3V'(2*128²) =96.
(V' :racine cubique) | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Lun 28 Juil 2008, 22:22 Lun 28 Juil 2008, 22:22 | |
| solution postée.
par AM-GM on a:a²+2ab+2ab+4b²+c²+c²>=6rac(6)(16(abc)^4))=96! | |
|
  | |
abdellatif
Féru

 Nombre de messages : 42 Nombre de messages : 42
Age : 35
Date d'inscription : 15/06/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Mar 29 Juil 2008, 17:23 Mar 29 Juil 2008, 17:23 | |
| bonjour
solution postee
solution non trouver | |
|
  | |
y-a-ss-i-n-e
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 33
Localisation : maroc
Date d'inscription : 21/12/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Mar 29 Juil 2008, 20:18 Mar 29 Juil 2008, 20:18 | |
| Solution postée.
solution non trouver | |
|
  | |
badr_210
Expert grade2

 Nombre de messages : 327 Nombre de messages : 327
Age : 33
Localisation : Sidi Slimane
Date d'inscription : 07/07/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Mer 30 Juil 2008, 12:33 Mer 30 Juil 2008, 12:33 | |
| السلام عليكم solution postée . solution de badr_210 on a : 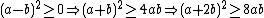 donc : 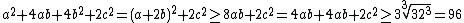 | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Mer 30 Juil 2008, 13:14 Mer 30 Juil 2008, 13:14 | |
| The best solution  (a²+4ab+2b²+2c²) = (a+2b)²+2c² ) >= (a+2b+c)²/(1+1/2) >= 2/3*(3(2abc)^1/3)² = 96 (Cauchy-Shwartz + IAG ) (a²+4ab+2b²+2c²) = (a+2b)²+2c² ) >= (a+2b+c)²/(1+1/2) >= 2/3*(3(2abc)^1/3)² = 96 (Cauchy-Shwartz + IAG ) | |
|
  | |
mohamed_01_01
Expert grade1

 Nombre de messages : 465 Nombre de messages : 465
Age : 34
Date d'inscription : 07/09/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Mer 30 Juil 2008, 23:42 Mer 30 Juil 2008, 23:42 | |
| solution postée
a²+4b²+c²>=3*(4*(abc)²))^1/3=3*2^4 ===>a²+4b²+c²>=3*2^4 (*)
4ab+c²+2^4>=4ab+8c>=2rac(4*8*abc)=2*2^5=2^6
===>4ab+c²>=2^6-2^4=2^4(4-1)=3*2^4 (**)
(*)+(**) ===> a²+4ab+4b²+c²>=3*2^4+3*2^4=96 | |
|
  | |
ilham_maths
Maître

 Nombre de messages : 130 Nombre de messages : 130
Age : 34
Localisation : Casablanca.
Date d'inscription : 06/08/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Jeu 31 Juil 2008, 18:05 Jeu 31 Juil 2008, 18:05 | |
| bonjour!
solution postée.
bonjour!
D'aprés l'inégalité remarquable du moyennes on a:3abc=<3((a+b+c)/3)^3=<3racine((a^2+b^2+c^2)/3).donc 3abc=< √((3(a^2+b^2+c^2))./1 d'une autre coté: a^2+b^2+c^2=<(a+b+c)^2 d'ou' racine(3(a^2+b^2+c^2))=<racine(3)x(a+b+c)./2
racine(3)a=<a^2+4ab,racine(3)b=<4b^2 et racine(3)c=<2c^2avec la sommation racine(3)x(a+b+c)=<a^2+4ab+4b^2+2c^2./3.de 1/ 2/ et /3 on déduit que 3abc=<a^2+4ab+4b^2+2c^2.alors 96=<a^2+4ab+4b^2+2c^2.
ilham_maths!! | |
|
  | |
joystar1
Maître
 Nombre de messages : 148 Nombre de messages : 148
Age : 35
Date d'inscription : 17/03/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Jeu 31 Juil 2008, 19:19 Jeu 31 Juil 2008, 19:19 | |
| salut solution postée
a²+4ab+4b²+2c²=a²+2ab+2ab+4b²+c²+c²>=6*[(abc)^4*16]^(1/6) (AM-GM)=6*[32^4*16]^(1/6)
32^(4/6)=32^(2/3)=2^(10/3)=2^(3+1/3)=8*2^1/3
16^(1/6)=2^(2/3)
d'ou le second membre de l'inegalité est:6*8*2=96 | |
|
  | |
huntersoul
Expert sup

 Nombre de messages : 1373 Nombre de messages : 1373
Age : 33
Localisation : In my mind
Date d'inscription : 19/02/2007
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Dim 03 Aoû 2008, 00:22 Dim 03 Aoû 2008, 00:22 | |
| solution postée
j'ai pas reussi a ouvrir la pièce jointe (administration ) | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Dim 03 Aoû 2008, 17:11 Dim 03 Aoû 2008, 17:11 | |
| Solution postée
Bonjour
a²+4ab+4b²+2c²=(a²+2ab+4b²)+2ab+2c²>=8ab+2c²=256/c+2c²>=96
A+ | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Sam 30 Aoû 2008, 19:19 Sam 30 Aoû 2008, 19:19 | |
| salut
solution postée
posons S le coté gauche de l inégalitéa²+4b²>=4abdonc :S>=4ab+4ab+2c²>=3*(32*abc²)^1/3 (AM-GM) =3(abc)^3/3=3*32=96 h-o-u-s-s-a-m | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  Lun 01 Sep 2008, 17:10 Lun 01 Sep 2008, 17:10 | |
| salut. solution posté la solution de probleme de la semaine n°144: on a:  et avec AM-GM:  d'ou l'inegalité desiré | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°144 (28/07/2008-03/08/2008) Sujet: Re: problème N°144 (28/07/2008-03/08/2008)  | |
| |
|
  | |
| | problème N°144 (28/07/2008-03/08/2008) |  |
|
