| | problème N°72 de la semaine (12/03/2007-18/03/2007) |  |
|
+4Kendor aissa abdelbaki.attioui samir 8 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: problème N°72 de la semaine (12/03/2007-18/03/2007)  Lun 12 Mar 2007, 13:00 Lun 12 Mar 2007, 13:00 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Lun 12 Mar 2007, 13:05 Lun 12 Mar 2007, 13:05 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Lun 12 Mar 2007, 14:19 Lun 12 Mar 2007, 14:19 | |
| Bonjour
Solution postée
voici la solution d'abdelbaki
Bonjour
Pour k>=1, soit a_k le plus petit élément du kiéme ensemble
==> a_(k+1)=a_k+k
mais a_1=1 ==> a_k=k(k-1)/2+1
==> S_k= a_k+(a_k+1)+...+(a_k+k-1)=k(a_k +(k-1)/2)=k(1+(k²-1)/2)
==> 2S_k=k(k²+1)
2(S_1+S_3+...+S_(2n-1))= 1^3+3^3+...+(2n-1)^3+ (1+3+...+(2n-1))
1+3+...+(2n-1)= (1+2+...+2n)-2(1+2+...+n)=n(2n+1)-n(n+1)=n²
1^3+3^3+...+(2n-1)^3= (1^3+2^3+...+(2n)^3) -8(1+2^3+...+n^3)=n²(2n+1)²-2n²(n+1)²
=n²(2n²-1)=2n^4-n²
==> S_1+S_3+...+S_(2n-1)=n^4
A+
| |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: problème N°72 Sujet: problème N°72  Mer 14 Mar 2007, 09:04 Mer 14 Mar 2007, 09:04 | |
| salam
sulotion postée
voici la solution d'aissasalam
pour tout k entier >=2 le k ième ensemble de la partition commence par le nombre k(k-1)/2:
par recurrence sur n :
si n=1 on a bien S_1=1^4.
supposons que : S_1+S_3+....+S_(2n-1)=n^4
alors: S_1+S_3+...+S_(2n-1)+S-(2n+1)= n^4+[n(2n+1)+1+....+
n(2n+1)+2n+1 ]= n^4 +n(2n+1)²+(2n+1)(n+1)
=n^4+4n^3+6n^2+4n+1
=(n+1)^4 .
donc pour tout n de NI* S_1+S_3+...+S_(2n-1)=n^4. CQFD
( rq :1+2+...+2n+1=(2n+2)(2n+1)/2=(n+1)(2n+1)).
من اراد العلي بغير جد سيدركه حين يشيب الغراب | |
|
  | |
Kendor
Féru
Nombre de messages : 64
Localisation : Malakoff (92240)
Date d'inscription : 13/12/2005
 |  Sujet: Solution au problème de la semaine n°72 par Kendor Sujet: Solution au problème de la semaine n°72 par Kendor  Mer 14 Mar 2007, 12:32 Mer 14 Mar 2007, 12:32 | |
| Bonjour! Solution postée! voici la solution de Kendor
IN est la réunion des E_n,avec E_n={a_n,a_n+1,…,a_n+n-1}a_(n+1)=a_n+nD’où a_n=1+n(n-1)/2s_n=na_n+n(n-1)/2 Soit S_n la somme des s_(2k-1),pour k variant de 1 à n. Raisonnons par récurrence sur n :
- Si S_n=n^4,calculons S_(n+1)
S_(n+1)=S_n+s_(2n+1)=S_n+(2n+1)a_(2n+1)+(2n+1)n=S_n+(2n+1)[1+(2n+1)n]+(2n+1)nDonc S_(n+1)=S_n+2n+1+n(2n+1)^2+n(2n+1)=S_n+2n+1+4n^3+4n^2+n+2n^2+nDonc S_(n+1)=S_n+4n^3+6n^2+4n+1=n^4+4n^3+6n^2+4n+1=(n+1^4 Donc,quelque soit n entier naturel non nul,S_n=n^4.CQFD Ciao !A+ Kendor | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Mer 14 Mar 2007, 14:56 Mer 14 Mar 2007, 14:56 | |
| Bonjour
Solution postée
voici la solution de khamaths
montrons cet inégalitée par récurrence sur n
(*) Pour n=1: k=1===> S1=1=1^4
(*)Supposons que: S1+S3+...+S_{2n-1}=n^4 et mq qu'elle est vraie pour n+1
O n a : S1+S3+..+S_{2n+1} = n^4 + S_{2n+1}
Or S_{2n+1} =Sigma_k=1^{2n+1} [(2n+1)n+k]
= (2n+1)(2n²+n) +(n+1)(2n+1)
=4n^3+6n² + 4n +1
D'où : S1+S3+....+S_{2n+1} = (n+1)^4
D'où le résultat | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Jeu 15 Mar 2007, 23:07 Jeu 15 Mar 2007, 23:07 | |
| bonsoir ! solution postée  voici la solution de selfrespectposons I_1={1} ,I_2={2,3} ,I_3={4,5,6} ,I_4={7,8,9,10}... voici la solution de selfrespectposons I_1={1} ,I_2={2,3} ,I_3={4,5,6} ,I_4={7,8,9,10}...
et posons 
montrons par réccurence sur  que que  est juste est juste 
[color=red]*P(1):est vraie [color:57a0=red:57a0]*supposons P(n) est vraie et montrons que  est vraie .  on a  calculons  on remarque que I_(2n+1)={(2n+1)n+1,(2n+1)n+2,.......(2n+1)(n+1)} alors   alors  est vraie !! | |
|
  | |
rockabdel
Maître
Nombre de messages : 264
Date d'inscription : 15/09/2006
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Dim 18 Mar 2007, 12:01 Dim 18 Mar 2007, 12:01 | |
| Solution postée voici la solution de Rockabdel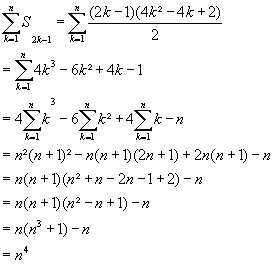 | |
|
  | |
Weierstrass
Expert sup

 Nombre de messages : 2079 Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  Dim 18 Mar 2007, 19:25 Dim 18 Mar 2007, 19:25 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007) Sujet: Re: problème N°72 de la semaine (12/03/2007-18/03/2007)  | |
| |
|
  | |
| | problème N°72 de la semaine (12/03/2007-18/03/2007) |  |
|
