| | << GRanD Jeu D'été 2009 >> |  |
|
+35kobica migao epsilon kogu La volonté Galois 94 MohE memath jalalium EINSTEINIUM Boomer Perelman merkam botmane elhor_abdelali milor18 amjad92b Matherror majdouline mathema Conan Hajar'S Intelligence Artificielle oussama1305 houssa mhido1992 {}{}=l'infini n.naoufal maganiste youna ADISON Figo L miss-Design MouaDoS 39 participants |
|
| Auteur | Message |
|---|
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 16:59 Mer 05 Aoû 2009, 16:59 | |
| Salut, ---------------------------------------- calculer en fonction de n la somme: 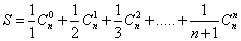 | |
|
  | |
kogu
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 33
Localisation : www.89.com
Date d'inscription : 10/06/2009
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 17:48 Mer 05 Aoû 2009, 17:48 | |
| Salut miss-Design , tu peux me dire d'où t'as eu l'idée de l'équation qui t'as permet de deduire que la divisibilité existe ?? | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 18:13 Mer 05 Aoû 2009, 18:13 | |
| j'ai du utiliser la factorisation de a^n+b^n et a^n-b^n
plusieurs fois en essayant à chaque fois de trouver un facteur commun c'est tt , et pour le 5 quand j'ai simplifier la dernière expression qui m'a resté je l'ai trouvé c tt | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 22:29 Mer 05 Aoû 2009, 22:29 | |
| salam
remarque1:
Somme des C(n,p) , p : 0 ---------> n , vaut 2^n
remarque 2 :
C(n+1 , p+1) = (n+1)/(p+1) . C(n,p)
===> 1/(p+1) . C(n,p) = 1/(n+1) .C(n+1 , p+1)
en sommant p: 0 --------> n
on obtient : 1/(n+1).[ somme des C(n+1 , p+1) pour p :0--------->n]
= 1/(n+1). [ 2^(n+1) - C(n+1, 0)]
= [2^(n+1) - 1] / (n+1)
..................................................... | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 23:18 Mer 05 Aoû 2009, 23:18 | |
| | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Mer 05 Aoû 2009, 23:31 Mer 05 Aoû 2009, 23:31 | |
| revenons à la géométrie:
Un hexagone régulier ABCDEF.
M € [AC] ; N € [CE] tels que :
AM/AC = CN/CE = k
Trouver k pour que : B , M , N soient alignés.
......................................................................... | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Jeu 06 Aoû 2009, 22:32 Jeu 06 Aoû 2009, 22:32 | |
| alors aucune tentative ???
. | |
|
  | |
Matherror
Maître
 Nombre de messages : 81 Nombre de messages : 81
Age : 32
Date d'inscription : 09/04/2009
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Ven 07 Aoû 2009, 11:34 Ven 07 Aoû 2009, 11:34 | |
| Soit ABCDEF un hexagone régulier de côté a.
ABC et CDE et EFA sont des triangles identiques.
==> AC = CE = AE.
==> Les angles de ACE sont tous égaux à 60° et AM = CN = kAC.
Selon le théorème d'Al Kashi dans ABC, AC² = 2a² - 2a².cos120° = 3a²
==> AM² = 3k²a²
Selon le théorème d'Al Kashi dans ABM, ==> BM² = a²+AM² - 2a.AM.cos30°
==> BM² = (3k²+1)a² - 2√3ka².cos30°
==> BM² = (3k²+1)a² - 3ka².
==> BM² = (3k² - 3k + 1)a²
D'autre part, selon le théorème d'Al Kashi dans CMN,
MN² = CM² + CN² - 2CM.CN.cos60°
==> MN² = 3(1-k)²a² + 3k²a² - [3k(1-k)a²]
==> MN² = 3(1-k)(1-2k)a² + 3k²a²
==> MN² = 3[(1-k)(1-2k) + k²]a²
==> MN² = 3(3k² - 3k + 1)a²
D'autre part, BCN est rectangulaire en C.
Donc, selon le théorème de Pythagore dans BCN, BN² = a² + 3k²a²
==> BN² = (3k² + 1)a².
Or, B et M et N sont alignés implique que BM + MN = BN
==> √(3k² - 3k + 1)[(1+√3)]a = √(3k² + 1)a
==> √(3k² - 3k + 1)[(1+√3)] = √(3k² + 1)
==> (3k² - 3k + 1)(1+√3)² = (3k² + 1)
==> (3k² + 1)[(1+√3)² - 1] - 3k(1+√3)² = 0
==> (3+2√3)(3k² + 1) - 6(2+√3)k = 0
==> 3(3+2√3)k² - 6(2+√3)k + (3+2√3) = 0
Équation classique du second degré, le delta est nul et la solution est unique et est k = √3/3.
Sauf erreur. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Ven 07 Aoû 2009, 21:48 Ven 07 Aoû 2009, 21:48 | |
| oui parfait
moi je propose une solution avec les angles uniquement
..............................................
on part de B, M , N alignés
on poursuit la même idée :
P € [EA] tel que : EP = k.EA
1ère étape : on montre que MNP est équilatéral
2ème étape : soit O le centre de l'hexagone.
c'est aussi le centre de MNP.
3ème étape : les triangles AOM et ABM sont isométriques
===> les angles :
MAO + AOM = OMC=OMN + NMC
===> 30°+ AOM = 30°+ NMC
==> AOM=NMC ===> ABM= AMB =====> AMB isocèle en A
conclusion : k = AM/AC = AB/AC = AB/ABV(3) = 1/V(3).
................................... | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Ven 07 Aoû 2009, 22:01 Ven 07 Aoû 2009, 22:01 | |
| alors à toi MATHERROR..........
. | |
|
  | |
Matherror
Maître
 Nombre de messages : 81 Nombre de messages : 81
Age : 32
Date d'inscription : 09/04/2009
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 08 Aoû 2009, 10:19 Sam 08 Aoû 2009, 10:19 | |
| Soient n un entier naturel supérieur ou égal à 1 et (Θ₁, Θ₂, Θ₃ ... Θn) des réels et c une constante de IN* tels que tan²Θ₁ + tan²Θ₂ + tan²Θ₃ + ... tan²Θn = c.
Déterminez ( en fonction de c ) la valeur maximale de n pour laquelle la valeur minimale de (tan²Θ₁.cosΘ₁)² + (tan²Θ₂.cosΘ₂)² + ... (tan²Θn.cosΘn)² soit 1. | |
|
  | |
botmane
Expert grade1

 Nombre de messages : 411 Nombre de messages : 411
Age : 32
Localisation : surement chez moi
Date d'inscription : 03/04/2007
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 08 Aoû 2009, 15:50 Sam 08 Aoû 2009, 15:50 | |
| slt tous le monde; je tente (pas sûr):
en utilisant: 1/cos²ai=tan²ai+1
on trouve: sigma(tan²ai*cosai)²=c-n+sigma(1/(tan²ai+1))i=1>>n =1
on prend:
f(x)=1/(tan²x+1)
f'(x)=0 <==> 2tanx*(tan²x+1)=0
min(f(x))=-1 ou min(f(x))=-1/2
alors sigma(...)=-n ou sigma(...)=-n/2
alors :
c-n-n=1 <==> n=(c-1)/2
ou
c-n-n/2=1 <==> n=(2c-1)/3 | |
|
  | |
botmane
Expert grade1

 Nombre de messages : 411 Nombre de messages : 411
Age : 32
Localisation : surement chez moi
Date d'inscription : 03/04/2007
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 08 Aoû 2009, 20:37 Sam 08 Aoû 2009, 20:37 | |
| maintenant, reste à étudier les cas de c ( divisible par 3, paire, impaire....)
es-ce-c'est juste? | |
|
  | |
botmane
Expert grade1

 Nombre de messages : 411 Nombre de messages : 411
Age : 32
Localisation : surement chez moi
Date d'inscription : 03/04/2007
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Lun 10 Aoû 2009, 19:33 Lun 10 Aoû 2009, 19:33 | |
| où etes vous passés les matheux? il n'y a plus de jeu d'été ? | |
|
  | |
phenix
Féru

 Nombre de messages : 31 Nombre de messages : 31
Age : 30
Localisation : rabat
Date d'inscription : 24/08/2009
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Lun 24 Aoû 2009, 12:31 Lun 24 Aoû 2009, 12:31 | |
| moi ossi je di a miss-design ke cé faux pr le deuxieme exo1et 0 ne sont pa des soluces | |
|
  | |
maths-fati-physique
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 30
Date d'inscription : 05/09/2009
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 05 Sep 2009, 16:37 Sam 05 Sep 2009, 16:37 | |
| slt moi aussi je s8 d'accord avec figo | |
|
  | |
houcinemm
Habitué
 Nombre de messages : 22 Nombre de messages : 22
Age : 33
Date d'inscription : 06/10/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Ven 11 Sep 2009, 19:51 Ven 11 Sep 2009, 19:51 | |
| calculer
lim (rac(sin2nx/1+cosnx))/4n²x²-pi²
x->pi/2n | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 12 Sep 2009, 11:35 Sam 12 Sep 2009, 11:35 | |
| Je crois qu'il y'a une erreur : ... 1+cos2nx ...
Résultat : x->(pi/2n)- : -infini
x->(pi/2n)+ : +infini | |
|
  | |
houcinemm
Habitué
 Nombre de messages : 22 Nombre de messages : 22
Age : 33
Date d'inscription : 06/10/2008
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  Sam 12 Sep 2009, 12:10 Sam 12 Sep 2009, 12:10 | |
| il n'y a pas d'erreur
résultat c'est : - infini | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: << GRanD Jeu D'été 2009 >> Sujet: Re: << GRanD Jeu D'été 2009 >>  | |
| |
|
  | |
| | << GRanD Jeu D'été 2009 >> |  |
|
